Для достоверной интерпретации экспериментальных спектроскопических данных требуется знать ширину каналов заселения флуоресцентных состояний и, следовательно, полную ширину промежуточных состояний, если таковые существуют. В частности, представляют интерес полные ширины промежуточных ионных состояний типа KrIII 4p-3 nl, которые могут проявляться во флуоресцентных спектрах после 3d ионизации атома Kr или его возбуждения в резонансное KrI 3d-1 np состояние после их автоионизационных распадов. Вполне очевидны радиационные каналы, представленные одноэлектронными дипольными переходами типа KrIII 4p-3nl→KrIII 4p-3n'l' или KrIII 4p-3nl→KrIII 4p-2, в которых меняет состояние только оптический электрон nl. Однако можно указать на существование и других не столь тривиальных дипольных переходов из KrIII 4p-3nl, именно KrIII 4p-3nl→KrIII 4s-14p-1, в которых изменяются состояния сразу двух электронов благодаря корреляционным взаимодействиям. Схематическое изображение двухэлектронного корреляционного перехода типа i1i2i3 nl→i1,2,3 f n'l' (например, KrIII 4p-3nl→KrIII 4s-14p-1) c участием возбужденного электрона nl представлено на рис.1. В этих переходах одна из конечных вакансий, а именно 4s-вакансия, лежит в более глубокой оболочке, чем начальные 4p-вакансии, т.е. реализуется предсказанный нами ранее работах в [1,2] механизм «углубления» или «встречного движения» вакансий. Заметим, что одна из начальных 4p-дырок не принимает непосредственного участия в этих переходах - остается «наблюдателем», в то время как две другие 4p-дырки заполняются внешним np- и внутренним 4s-электронами. Поскольку конечная 4s-вакансия лежит ниже по энергии, чем начальные 4p-дырки, излучаемый фотон имеет меньшую энергию, чем в обычном однофотонном распаде двухдырочного состояния [3].
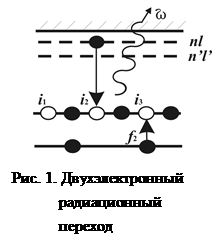
Для анализа относительной ширины двухэлектронных переходов рассмотрены также «некорреляционные» переходы типа KrIII 4p-3 np→KrIII 4p-3 n's/d, в которых меняется состояние только оптического электрона. Показано, что ширина некоторых корреляционных переходов сравнима с «некорреляционными» (далее c- и nс-переходы, соответственно).
Вообще говоря, каналы заселения могут содержать и более сложные корреляционные переходы, в которых сразу три электрона меняют свои состояния, например, трехэлектронные радиационные переходы [8] типа KrII 4s-2 nl→4p-2 n'l'.
Основные положения теории
Вероятность радиационного перехода между состояниями ![]() и
и ![]() (здесь γ обозначает весь остальной набор квантовых чисел) выражается известным соотношением
(здесь γ обозначает весь остальной набор квантовых чисел) выражается известным соотношением
![]() ,
,
где ![]() – энергия излучаемого фотона,
– энергия излучаемого фотона, ![]() – постоянная тонкой структуры,
– постоянная тонкой структуры, ![]() – приведенный дипольный матричный элемент. Согласно известным правилам отбора для дипольных переходов, орбитальный момент оптического электрона меняется на единицу, (
– приведенный дипольный матричный элемент. Согласно известным правилам отбора для дипольных переходов, орбитальный момент оптического электрона меняется на единицу, (![]() ), а изменение полных угловых моментов системы удовлетворяет соотношениям
), а изменение полных угловых моментов системы удовлетворяет соотношениям ![]() =0,1 и
=0,1 и ![]() =0.
=0.
Суммарная ширина nc-переходов KrIII 4p-3 nl→KrIII 4p-3 n'l' видимого диапазона может быть с достаточной степенью точности вычислена в низшем порядке ТВ по межэлектронному взаимодействию как сумма вероятностей переходов оптического электрона nl при неизменном терме ионного остова KrIII 4p-3[LiSi=LfSf]. Переходы с изменением терма остова (LiSi¹LfSf) определяются диаграммами более высокого порядка ТВ, вклад которых значительно меньше. Поэтому здесь учтены только nc-переходы без изменения терма. Тем не менее количество различных nc-переходов с изменением терма остова довольно велико, так что их суммарный вклад в полную ширину, несмотря на малость их парциальных ширин, может оказаться заметным. Это следует учитывать при интерпретации экспериментальных данных.
Рассмотрим с-переходы вида i1i2i3 n→i1,2,3 f n'. Заметим, что в этих переходах одна из начальных вакансий не меняется, т.е. является «наблюдателем». Парциальным амплитудам низшего неисчезающего порядка ТВ
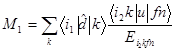
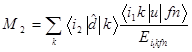
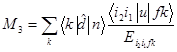
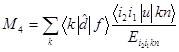
соответствуют фейнмановские диаграммы на рис. 2.
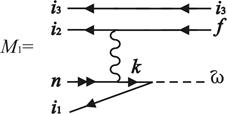
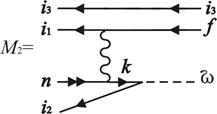
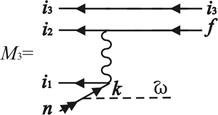
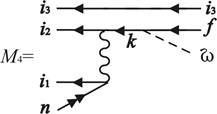
Рис. 2. Фейнмановские диаграммы (плюс обменные к ним) для c-переходов типа
i1i2i3 n→i1,2,3 f n'. Вакансия i3 выступает в роли «наблюдателя»
Суммирование проводится по промежуточным дырочным и дискретным возбужденным состояниям и включает интегрирование по состояниям непрерывного спектра. Так как любая из трех i1, i2, i3 вакансий может играть роль «наблюдателя» в переходе типа i1i2i3 n→i1,2,3 f n', к диаграммам рис. 2 добавляются аналогичные диаграммы, получаемые циклической перестановкой индексов начальных вакансий. Для переходов 4p-3 nl→4s-1 4p-1 с тремя эквивалентными 4p-вакансиями расчет упрощается введением множителя 3 на этапе вычисления ширины переходов. Диаграммы учитывают корреляции в начальном и конечном состояниях в рамках первого порядка ТВ. Определенная часть корреляционных взаимодействий высших порядков ТВ может быть учтена эффективно [4] выбором потенциала, в котором вычисляются волновые функции.
Формулы для вычисления угловых множителей парциальных амплитуд получены в приближении LS-связи при следующей схеме сложения моментов:
![]() , где N – нормировочные множители,
, где N – нормировочные множители, ![]() – генеалогические коэффициенты. Для исследуемых переходов 4p-3 nl→4s-14p-1 нормировочные множители равны Nin=
– генеалогические коэффициенты. Для исследуемых переходов 4p-3 nl→4s-14p-1 нормировочные множители равны Nin=![]() , Nfn=1. Так что ВФ начального состояния, в зависимости от терма ионного остова LiSi, приобретают вид:
, Nfn=1. Так что ВФ начального состояния, в зависимости от терма ионного остова LiSi, приобретают вид:
![]() ,
,
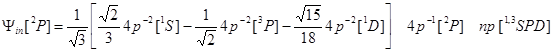 ,
,
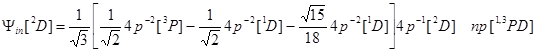 .
.
Окончательные выражения для орбитальных Yα и спиновых A, B множителей парциальных амплитуд Mα, полученные в рамках изложенной в [6] методики имеют вид:
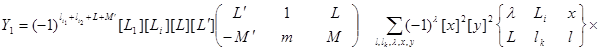
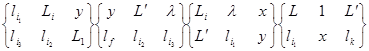 ,
,
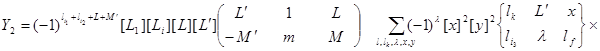
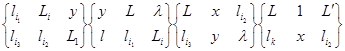 ,
,
![]()
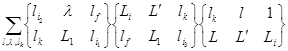
![]()
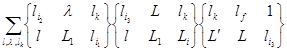
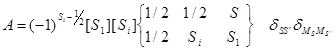 ,
, ![]() .
.
Основные результаты и обсуждение
При вычислении амплитуд переходов волновые функции возбужденных электронов nl каждого состояния KrIII 4p-3[LiSi] nl [LS] рассчитаны в «замороженном» поле ионного остова 4p-3[LiSi]. При суммировании по k учтены, кроме дырочных, по 4 дискретных возбуждения, а также состояния непрерывного спектра, рассчитанные в 35 точках по энергии для каждого разрешенного правилами отбора значения орбитального момента lk. Для вычисления энергии переходов использованы энергии LS-состояний, полученные на основе статистического усреднения экспериментальных [9] энергий LSJ-состояний. Достоверность вычисления приведенных дипольных матричных элементов ![]() протестирована расчетом матричных элементов для переходов 2p-1 3s→2p-1 3p в Ne и сравнением с имеющимися теоретическими и экспериментальными данными ([5] и ссылки в ней).
протестирована расчетом матричных элементов для переходов 2p-1 3s→2p-1 3p в Ne и сравнением с имеющимися теоретическими и экспериментальными данными ([5] и ссылки в ней).
Проведен расчет характеристик дипольных переходов из состояний KrIII 4p-3[LiSi] 5p [LS] в состояния KrIII 4p-3[LfSf= LiSi] 5s[L'S], KrIII 4p-3[LfSf= LiSi] 4d[L'S] (всего 55 nс-переходов) и KrIII 4s-1 4p-1 [L'S] (всего 11 nс-переходов), а также из KrIII 4p-3[LiSi] 6p [LS] в состояния KrIII 4p-3[LfSf= LiSi] ns[L'S] (n=5,6), KrIII 4p-3[LfSf= LiSi] nd[L'S] , n=4,5 (всего 92 nс-перехода) и KrIII 4s-1 4p-1 [L'S] (всего 11 nс-переходов). В Таблице 1 приведены энергия ω (эВ) и ширина G (эВ) только c-переходов, вычисленная в форме длины и в форме скорости, и относительная ширина η (% от суммарной рассчитанной радиационной ширины начального состояния). Анализируя ширину переходов из 4p-3[LiSi] 5p [LS], можно сделать следующие выводы:
- большинство nc-переходов в состояния конфигурации 4p-35s более вероятны, чем в 4p-3 4d;
- более вероятны nc-переходы в состояния с большим статистическим весом (2L'+1)(2S+1);
- вероятности с-переходов сравнительно малы, их относительный вклад составляет от десятых до нескольких процентов полной ширины соответствующей группы переходов;
- ширина с-переходов примерно соответствует таковым из наиболее слабых nc-переходов;
- ширина переходов, вычисленная в форме длины и в форме скорости, иногда заметно отличается (что естественно при использовании приближения ХФ), однако величина относительного вклада мало зависит от формы вычисления.
Экспериментальная энергия ω (эВ) [9,10] и вычисленная ширина G (эВ) дипольных корреляционных переходов в форме длины (R) и в форме скорости (V) и относительная ширина η (%) с-перехода
|
4p-3[LiSi] 5p[LS] |
Терм 4s4p5 |
ωэксп (эВ) [10] [9] |
G (10-6 эВ) R ‑ форма |
η (%) |
G (10-6 эВ) V ‑форма |
η (%) |
|
|
4S 5p 3P |
4s4p5 3P |
8.064 |
7.717 |
0.0003 |
0.1 |
0.0000 |
0.0 |
|
2P 5p 1S |
4s4p5 1P |
8.612 |
|
0.0067 |
0.5 |
0.0003 |
0.1 |
|
2P 5p 1P |
4s4p5 1P |
8.372 |
8.727 |
0.0142 |
1.7 |
0.0033 |
0.4 |
|
2P 5p 1D |
4s4p5 1P |
8.722 |
8.709 |
0.0034 |
0.3 |
0.0017 |
0.1 |
|
2P 5p 3S |
4s4p5 3P |
11.612 |
11.270 |
0.3190 |
30.0 |
0.1321 |
12.6 |
|
2P 5p 3P |
4s4p5 3P |
12.081 |
11.620 |
0.0409 |
2.9 |
0.0038 |
0.4 |
|
2P 5p 3D |
4s4p5 3P |
11.649 |
11.305 |
0.0104 |
0.8 |
0.0066 |
0.7 |
|
2D 5p 1P |
4s4p5 1P |
6.492 |
6.477 |
0.0835 |
9.0 |
0.0338 |
4.5 |
|
2D 5p 1D |
4s4p5 1P |
7.572 |
7.565 |
0.0165 |
1.1 |
0.0017 |
0.2 |
|
2D 5p 3P |
4s4p5 3P |
10.908 |
10.007 |
0.36451 |
15.1 |
0.0454 |
3.3 |
|
2D 5p 3D |
4s4p5 3P |
9.659 |
9.457 |
0.0560 |
4.6 |
0.0184 |
1.9 |
|
4S 6p 3P |
4s4p5 3P |
13.761 |
13.414 |
0.0118 |
5.8 |
0.0016 |
1.0 |
|
2P 6p 1S |
4s4p5 1P |
12.644 |
|
0.1605 |
25.5 |
0.0401 |
12.4 |
|
2P 6p 1P |
4s4p5 1P |
14.358 |
14.713 |
0.0736 |
19.3 |
0.0395 |
15.5 |
|
2P 6p 1D |
4s4p5 1P |
14.473 |
14.460 |
0.0020 |
0.5 |
0.0006 |
0.2 |
|
2P 6p 3S |
4s4p5 3P |
17.686 |
17.344 |
0.3090 |
51.3 |
0.1765 |
37.0 |
|
2P 6p 3P |
4s4p5 3P |
17.920 |
17.459 |
0.1986 |
31.0 |
0.0832 |
23.7 |
|
2P 6p 3D |
4s4p5 3P |
17.670 |
17.326 |
0.0000 |
0.0 |
0.0000 |
0.0 |
|
2D 6p 1P |
4s4p5 1P |
12.517 |
12.502 |
0.2370 |
45.4 |
0.1225 |
36.5 |
|
2D 6p 1D |
4s4p5 1P |
12.903 |
12.896 |
0.0483 |
9.8 |
0.0164 |
5.3 |
|
2D 6p 3P |
4s4p5 3P |
16.637 |
15.736 |
0.5612 |
58.8 |
0.2146 |
47.2 |
|
2D 6p 3D |
4s4p5 3P |
15.722 |
15.520 |
0.0864 |
25.3 |
0.0438 |
13.0 |
В таблице также приведены результаты для переходов из более высоко возбужденных состояний KrIII 4p-3[LiSi] 6p [LS]. Переходы из этих состояний энергетически разрешены во все нижележащие состояния KrIII 4p-3[LfSf= LiSi] 5s,6s [L'S], KrIII 4p-3[LfSf= LiSi] 4d,5d[L'S] и KrIII 4s-1 4p-1 [L'S], так что общее количество nc-переходов практически вдвое больше, чем при распаде конфигурации 4p-3[LiSi] 5p. Наиболее сильными из nс-переходов оказались те, в которых не изменяется главное квантовое число возбужденного электрона. К ним относятся переходы в состояния 4p-3 6s, несмотря на более высокие энергии фотона в переходах
4p-3 6p→4p-3 5s. Среди переходов в 4p-3 nd более вероятны переходы в 4p-3 4d, чем в 4p-3 5d. Это означает, что, по крайней мере, некоторые из состояний 4p-3 4d могут довольно вероятно заселяться посредством nc-переходов не только из 4p-3 5p, но и из состояний 4p-3 6p.
Вероятность c-переходов 4p-3 6p→4s-14p-1 больше вероятности таких же переходов из 4p-3 5p в основном из-за больших энергий фотона. Это приводит и к большему относительному весу c-переходов при распаде 4p-3 6p→4s-14p-1. Однако при оценке полных ширин не учтены nc-переходы с изменением терма ионного остова, количество которых вдвое больше. Предположительно, их учет может привести к примерно такому же относительному вкладу с-переходов в полную ширину состояний 4p-3 6p, как и в таковую состояний 4p-3 5p.
В заключение отметим, что полученные результаты однозначно свидетельствуют о важности учета корреляционных взаимодействий при рассмотрении флуоресцентных распадов возбужденных состояний двукратных ионов. Нетривиальные корреляционные переходы типа KrIII 4p-3 nl→4s-1 4p-1 дают весьма заметный вклад в полную радиационную ширину начального состояния, а некоторые из них вполне могут конкурировать с переходами типа KrIII 4p-3 nl→Kr III 4p-3 n'l' видимого диапазона длин волн.
Рецензенты:
Шаповалов А.В., д.ф.-м.н., профессор, зав. кафедрой теоретической физики, Физический факультет, Научно-исследовательский Томский государственный университет, г. Томск;
Гриняев С.Н., д.ф.-м.н., профессор, кафедра теоретической и экспериментальной физики, Физико-технический институт, Научно-исследовательский Томский политехнический университет, г. Томск.



