На современных камнеобрабатывающих предприятиях, в промышленном и гражданском строительстве, а также в коммунальном хозяйстве и сфере услуг оценка качества обработанной поверхности изделия в настоящее время производится визуально, тактильно или способом профилометрирования [1, 5], что не отвечает современным требованиям.
В связи с этим, была поставлена задача по созданию программного обеспечения, позволяющего произвести оценку любого участка обработанной поверхности путем ее сканирования либо фотографирования в режиме макросъемки.
На основании раннее проведенных исследований и полученных экспериментальных данных было разработано автономное программное обеспечение для персональных компьютеров и мобильных платформ Android и IOS: «Программа для определения шероховатости поверхности камня » [4].
Так как двумерные изображения не несут в себе информации о глубинной составляющей поверхности камня, предлагается подход, основанный на выделении на исходном изображении локальных участков и соотнесении их к классам с различным уровнем шлифовки. После чего в зависимости от того, каких участков больше на изображении, происходит вывод об уровне шлифовки всей поверхности.
На начальном этапе входное изображения ![]() разбивается на
разбивается на ![]() областей
областей ![]() , где
, где ![]() . Значение
. Значение ![]() задается априорно и зависит от разрешения обучающей выборки и входного изображения
задается априорно и зависит от разрешения обучающей выборки и входного изображения ![]() . В данной работе значение
. В данной работе значение ![]() . После чего для каждого
. После чего для каждого ![]() фрагмента формируется вектор признаков (дескриптор). Для формирования данного вектора признаков был использован модифицированный текстурный оператор LBP.
фрагмента формируется вектор признаков (дескриптор). Для формирования данного вектора признаков был использован модифицированный текстурный оператор LBP.
Оригинальный LBP [6] оператор рассчитывается путем сравнения каждого пикселя вокруг центрального пикселя, принятого за пороговое значение, в локальной области размером 3 на 3 пикселя. Если центральный пиксель меньше или равен соседнему, то на его место записывается 1, иначе 0. В результате проделанной операции центральному пикселю соответствует 8-битный двоичный код, что показано на рисунке 1.
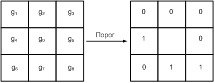
Рис. 1. LBP оператор
В работе [7], была предложена модификация оригинального оператора LBP [6]. Суть модификации заключается в увеличении радиуса пикселей, которые сравниваются с центральным пикселем. Также выделены 9 uniform patterns, которые несут наибольшую информативность о текстурных особенностях изображения (рисунок 2), а также позволяют сократить количество мало информативных бинов. Каждый из 9 uniform patterns соответствует своей текстурной особенности изображения, таких как ребра, углы и пятна.
Модифицированный LBP оператор может быть записан следующим образом:
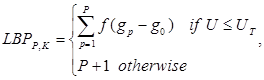
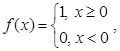
где ![]() – число соседей;
– число соседей;
![]() – радиус;
– радиус;
![]() – число переходов между 1 и 0;
– число переходов между 1 и 0;
![]() – пороговое значение на количество переходов.
– пороговое значение на количество переходов.
Таким образом, формируется гистограмма для локальной области, представляющая собой дескриптор для анализа локальных областей на изображении.
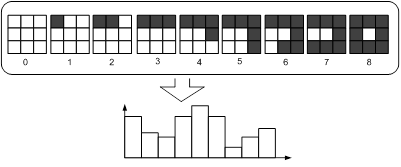
Рис. 2. Uniform patterns оператора LBP
Результат работы описанного оператора LBP приведен на рисунке 3.
 а)
а) 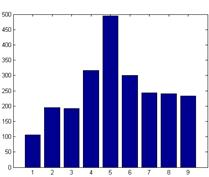 б)
б)
а) – фрагмент поверхности ![]() гранита, б) – гистограмма оператора LBP
гранита, б) – гистограмма оператора LBP
Рис. 3. Результат работы оператора LBP
Для классификации и соотнесения каждого участка к определенному уровню шлифовки используется метод опорных векторов (SVM) [2].
Для пояснения работы метода опорных векторов рассмотрим задачу классификации для объектов двух классов [7].
Пусть заданы:
- множество
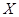 обучающих объектов, заданных векторами признаков
обучающих объектов, заданных векторами признаков 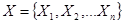 ,
, 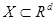 (
(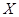 является подмножеством евклидова пространства размерности
является подмножеством евклидова пространства размерности 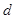 );
); - множество
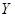 ответов для обучающих объектов:
ответов для обучающих объектов: 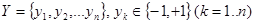 .
.
Тогда задача классификации состоит в построении такой функции ![]() (классификатора), в которой каждому вектору
(классификатора), в которой каждому вектору ![]() соответствует правильный ответ
соответствует правильный ответ ![]() .
.
В методе SVM в качестве функции ![]() выбрана плоскость, расстояния до которой ближайших векторов обоих классов равны (рисунок 4). Ближайшие точки-векторы называются опорными. При этом для всех объектов одного класса должно выполняться неравенство
выбрана плоскость, расстояния до которой ближайших векторов обоих классов равны (рисунок 4). Ближайшие точки-векторы называются опорными. При этом для всех объектов одного класса должно выполняться неравенство ![]() , а для всех объектов другого класса – неравенство
, а для всех объектов другого класса – неравенство ![]() [8, 9].
[8, 9].
Уравнение разделяющей плоскости имеет следующий вид:
![]()
где ![]() – размерность постранства признаков;
– размерность постранства признаков;
![]() – направляющий вектор;
– направляющий вектор;
![]() – скалярный порог.
– скалярный порог.
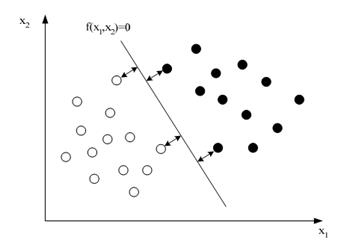
Рис. 4. Иллюстрация метода для двумерного пространства признаков
В методе опорных векторов выделяют два этапа: этап обучения и этап распознавания. На первом этапе из множества обучающих примеров отбираются опорные векторы, на основе которых строится разделяющая плоскость. Этап распознавания заключается в том, что на вход полученного классификатора подается пример ![]() , о классовой принадлежности которого ничего не известно. Классификатор должен дать ответ, к какому классу относится вектор
, о классовой принадлежности которого ничего не известно. Классификатор должен дать ответ, к какому классу относится вектор ![]() . Следует отметить, что метод SVM может применяться как для линейно разделимых образов, так и для линейно неразделимых. Во втором случае используется либо линейная разделяющая функция с мягкой границей (т.е. допускается минимальное количество ошибок классификации), либо осуществляется переход в пространство большей размерности, в котором образы становятся линейно разделимыми.
. Следует отметить, что метод SVM может применяться как для линейно разделимых образов, так и для линейно неразделимых. Во втором случае используется либо линейная разделяющая функция с мягкой границей (т.е. допускается минимальное количество ошибок классификации), либо осуществляется переход в пространство большей размерности, в котором образы становятся линейно разделимыми.
В данной работе для построения разделяющей гиперплоскости используется радиальная базисная функция
![]() при
при ![]() ,
,
где ![]() – текущий вектор;
– текущий вектор;
![]() – центральный вектор;
– центральный вектор;
![]() – нормализующий параметр;
– нормализующий параметр;
Пример использования данного ядра приведен на рисунке 5.
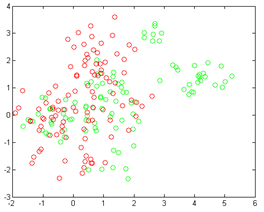 а)
а) 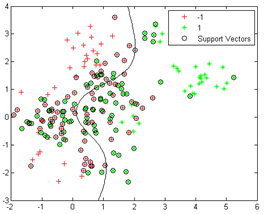 б)
б)
а) – входные значения, б) – пример разделяющей плоскости
Рис. 5. Иллюстрация построения разделяющей гиперплоскости
Для формирования обучающей выборки и построения разделяющей гиперплоскости было использованно 300 изображений с различным уровнем шлифовки. Размер изображений составляет ![]() пикселей.
пикселей.
Следует отметить, что для корректной работы алгоритма исходное изображение ![]() должно иметь разрешающую способность, не менее 600 точек на дюйм (600dpi).
должно иметь разрешающую способность, не менее 600 точек на дюйм (600dpi).
На заключительном этапе происходит оценка количества участков. В зависимости от того, с каким уровнем шлифовки участков больше , к такому классу и относится все изображение (делается вывод о принадлежности всего изображения к определенному уровню шлифовки).
Рецензенты:
Евстратов В.А., д.т.н., проф., зав. кафедрой «Машины и оборудование предприятий стройиндустрии», ШИ ЮРГПУ (НПИ) филиал ЮРГПУ им М.И. Платова, г. Шахты;
Кожемяченко А.В., д.т.н., проф., кафедры «Технические системы ЖКХ и сферы услуг» ИСОиП (филиал) ДГТУ, г. Шахты.



