Изучению вопросов надежности и работоспособности бурового и нефтепромыслового оборудования и инструмента посвящено значительное число аналитических и экспериментальных исследований, например [4,8,9,10]. Экспериментальные исследования нагруженности элементов вооружения шарошечного долота [2,3] показали, что осевая нагрузка, действующая на долото, распределяется неравномерно как по шарошкам, так и по венцам каждой шарошки. Результаты исследований зачастую противоречивы. Это объясняется весьма сложным характером процесса взаимодействия шарошечного долота с забоем, зависящим от большого числа факторов. Каждая шарошка, перекатываясь по забою, совершает сложное движение, складывающееся из вращения шарошки вокруг оси цапфы, вращения вокруг вертикальной оси долота, и вертикального поступательного движения по мере разрушения горной породы. Так как шарошки не связаны между собой кинематически, то количества зубков, одновременно находящихся в контакте с забоем, является случайной величиной, и соответственно, число связей долота с забоем также будет величиной переменной. Максимальное осевое усилие действует на зубок в момент перехода его через вертикальное положение. А так как зубки венцов шарошки смещены друг относительно друга по образующим, то можно предположить, что наиболее часто каждая шарошка будет контактировать с забоем лишь одним зубком, находящимся в вертикальном положении. Это допущение особенно справедливо при бурении крепких и особо крепких пород. Исходя из этого предположения, рассмотрим в статическом состоянии долото, каждая шарошка которого опирается на плоский забой одним зубком (Рис.1).
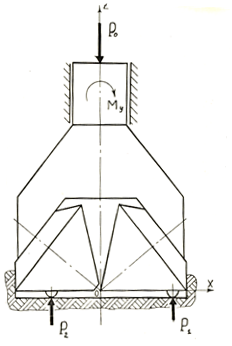
Рис.1.Схема сил, действующих на долото
Корпус долота и забой будем считать недеформируемым и, кроме того, примем, что долото при приложении нагрузки может перемещаться только параллельно оси Z без перекосов. При этом условии перемещения точек приложения усилий ![]() и
и ![]() относительно корпуса долота будут одинаковы. Данная система является один раз статически неопределимой, и для нахождения неизвестных величин
относительно корпуса долота будут одинаковы. Данная система является один раз статически неопределимой, и для нахождения неизвестных величин ![]() и
и ![]() мы можем использовать одно уравнение статики (1) и условие деформации системы (2):
мы можем использовать одно уравнение статики (1) и условие деформации системы (2):
![]() ;
;![]() (1)
(1)
![]() (2)
(2)
Для решения данной системы необходимо установить зависимость между величиной нагрузки, действующей на зубок шарошки и вертикальным перемещением этого зубка. Для трехшарошечного долота последовательность рассуждений остается такой же. Зависимости эти могут быть получены аналитически или экспериментально.
Конструкция опорных узлов всех шарошек долота одинакова и поэтому вертикальная жесткость каждой шарошки будет изменяться в зависимости от того, на каком радиусе долота находится зубок, контактирующий в данный момент с забоем. Рассмотрим одну секцию долота. На шарошку секции действует сила Р, параллельная оси долота на расстоянии R от оси долота (Рис.2). Необходимо определить вертикальное перемещение точки приложения силы.
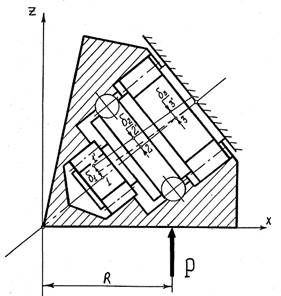
Рис.2.Расчетная схема шарошечного узла
Деформация корпуса шарошки будет незначительной по сравнению с деформацией цапфы и контактными деформациями в подшипниках и ею можно пренебречь. Таким образом, перемещение шарошки будет происходить за счет деформации цапфы и упругих контактных деформаций в подшипниках. Для того чтобы определить эти деформации, необходимо знать величины реакций в подшипниках. Решение данной задачи приведено в работах [5] и [6]. Используя результаты этого решения перейдем к определению величины вертикального перемещения точки А шарошки (Рис.3), в которой приложена сила Р. Пусть система координат ZOX будет неподвижной, а система ![]() подвижной, жестко связанной с шарошкой, начало координат которой находится в центре нижнего шарика. При приложение силы Р шарошка переместится и система координат
подвижной, жестко связанной с шарошкой, начало координат которой находится в центре нижнего шарика. При приложение силы Р шарошка переместится и система координат ![]() займет новое положение
займет новое положение ![]() .
.
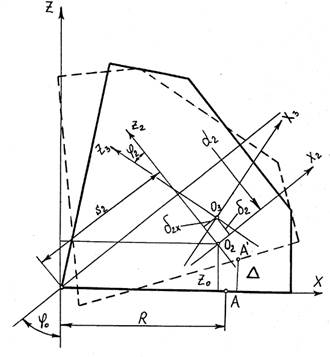
Рис.3. Схема к расчету вертикальных перемещений точки приложения внешней силы
Считаем, что радиальное перемещение точки ![]() нам известно [5]. Осевое перемещение точки
нам известно [5]. Осевое перемещение точки ![]() происходит под действием осевой силы в шариковом подшипнике
происходит под действием осевой силы в шариковом подшипнике![]() . Для определения осевого перемещения воспользуемся методикой, приведенной в работе
. Для определения осевого перемещения воспользуемся методикой, приведенной в работе ![]() . Поскольку мы приняли, что радиальные зазоры в подшипниках равны нулю, то первоначальный угол контакта шариков с беговыми дорожками также будет равен нулю. Для этого случая осевое перемещение подшипника
. Поскольку мы приняли, что радиальные зазоры в подшипниках равны нулю, то первоначальный угол контакта шариков с беговыми дорожками также будет равен нулю. Для этого случая осевое перемещение подшипника ![]() , фактический угол контакта шариков с беговыми дорожками
, фактический угол контакта шариков с беговыми дорожками ![]() и действующая осевая сила
и действующая осевая сила ![]() связаны зависимостями:
связаны зависимостями:
![]() ; (3)
; (3)
![]() (4)
(4)
Где:
![]() силовая характеристика подшипника
силовая характеристика подшипника
![]()
![]() коэффициент, зависящий от размеров подшипника.
коэффициент, зависящий от размеров подшипника.
Поскольку уравнение (4) нельзя решить в явном виде, то его решают приближенно, введя замену переменного ![]() х, и используя разложение в ряды тригонометрических функций
х, и используя разложение в ряды тригонометрических функций ![]() и
и ![]() учитывая в первом из них три, а во втором два члена. Тогда уравнение (4) преобразуется к виду:
учитывая в первом из них три, а во втором два члена. Тогда уравнение (4) преобразуется к виду:
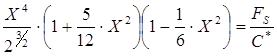 ; (5) /4.2.49/
; (5) /4.2.49/
Решение этого уравнения методом последовательных приближений
имеет вид:
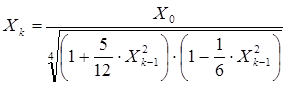 ; (6)
; (6)
Где: k = 1,2…
Проверка показала, что уже при k=1 значение ![]() практически не отличается от
практически не отличается от ![]() . По найденному значению угла контакта
. По найденному значению угла контакта ![]() определяем из выражения (3) искомое перемещение шарика
определяем из выражения (3) искомое перемещение шарика ![]() . Угол поворота
. Угол поворота ![]() системы координат Z3O3X3 может быть определен из рассмотрения радиальных деформаций в замковом шариковом и одном из радиальных подшипников (рис.2).
системы координат Z3O3X3 может быть определен из рассмотрения радиальных деформаций в замковом шариковом и одном из радиальных подшипников (рис.2).
 ; (7)
; (7)
При перемещении шарошки точка А займет новое положение – А1. Для определения величины вертикального перемещения точки А необходимо найти координату Z точки А1 в системе координат ZOX. Координаты точки А1 в сиcтеме координат Z3O3X3 можно определить:
![]() ; (8)
; (8)
![]() ;
;
Для определения координат точки А1 в системе ZОX запишем формулы перехода из системы координат Z3O3X3 в систему ZОX. Координаты точки А1 в системе Z3OsX3 определяется:
![]() ; (9)
; (9)
![]() ;
;
Тогда искомая величина Z , равная вертикальному перемещению точки А определится:
![]() ; (10) /4.2.53/
; (10) /4.2.53/
Где,
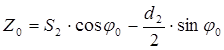 ; (11)
; (11)
Получить интересующие нас зависимости вертикального перемещения точки А от силы Р и радиуса ее приложения R в явном виде не представляется возможным. Поэтому эти зависимости были получена для опоры долота Ш215,9К-ПВ в виде таблицы значений при различных величинах Р и R.
По результатам расчетов построены графические зависимости вертикального перемещения шарошки от величины, действующего на шарошку усилия и радиуса его приложения, приведенные на Рис.4.
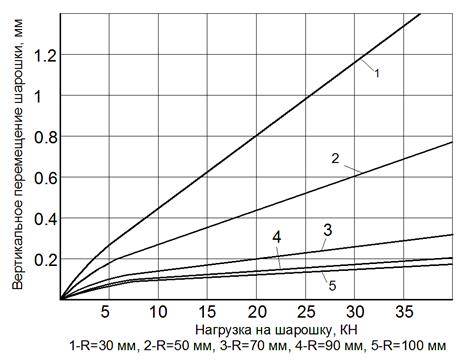
Рис.4. Расчетные зависимости вертикального перемещения шарошки от величины и радиуса приложения внешнего усилия
Как следует из приведенных графиков, изменение вертикального перемещения шарошки от действующего усилия имеет линейную зависимость при нагрузках Р![]() 10 кН. Зависимость вертикального перемещение шарошки от радиуса приложения усилия имеет более сложный характер. При увеличении радиуса до R = 90 мм величина деформации уменьшается, т.е. осевая жесткость системы возрастает.
10 кН. Зависимость вертикального перемещение шарошки от радиуса приложения усилия имеет более сложный характер. При увеличении радиуса до R = 90 мм величина деформации уменьшается, т.е. осевая жесткость системы возрастает.
При дальнейшем увеличении радиуса приложения нагрузки расчетная осевая жесткость системы вновь несколько снижается. Изменение осевой жесткости шарошечного узла при изменении радиуса приложения внешней нагрузки на шарошку определяется, очевидно, изменением напряженного состояния деталей опоры шарошки [7]. При изменении радиуса приложения внешней нагрузки происходит перераспределение нагрузки между подшипниками [5].
Предлагаемая методика аналитического исследования деформируемости деталей долота может использоваться для аналитической оценки загруженности венцов шарошек и оптимизации конструкции вооружения и опор шарошечного долота.
Рецензенты:
Долгушин В.В., д.т.н., профессор, директор Института промышленных технологий и инжиниринга ФГБОУ ВПО «Тюменский Государственный нефтегазовый университет», г. Тюмень;
Перевощиков С.И., д.т.н., профессор кафедры «Прикладная механика» ФГБОУ ВПО «Тюменский Государственный нефтегазовый университет», г. Тюмень.



