Общее направление исследований связано с развитием математических моделей трубопроводов, а также алгоритмов их численной реализации [3], разрабатываемых с целью изучения картины распространения упругих волн в материале трубопровода и подтверждения корректности основанной на методах вибродиагностики методики оценки остаточной работоспособности трубопроводов [5]. Разработанные в результате исследований математические и компьютерные модели динамических систем могут быть представлены в виде виртуальных прототипов, на основе которых разрабатываются расчетные методики проектирования металлургической продукции с применением современных CAD/CAE-систем; научно обосновываются методы вибродиагностики и дефектации готовой продукции высокотехнологичных предприятий.
В рамках текущего исследования основными решаемыми задачами стали:
-
разработка нестационарной конечно-элементной модели распространения упругих волн в материале трубопровода;
-
проведение серии вычислительных экспериментов для изучения картины распространения упругих волн, вызванных приложением импульсного силового воздействия с известными характеристиками;
-
определение динамического отклика системы в характерных точках;
-
отработка методов визуализации движения фронта волны, колебательного движения точек среды.
В работе методом конечных элементов создается компьютерная осесимметричная модель, математическая постановка которой представлена в работе [1], объект исследования (трубопровод) схематично представлен на рисунке 1.
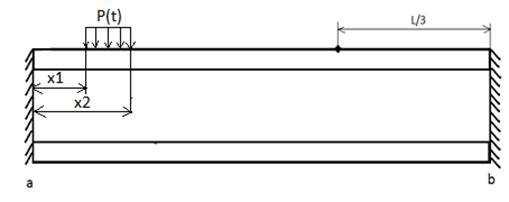
Рис. 1. Схема трубопровода, нагруженного импульсным воздействием
Применяются осесимметричные треугольные трехузловые конечные элементы с линейной аппроксимацией и двумя степенями свободы по перемещениям в каждом узле. Верификация разработанной компьютерной модели осуществляется двумя способами.
Верификация предложенных моделей
Прежде всего, осуществляется проверка корректности формирования глобальной матрицы жесткости, формирования глобального вектора сил и алгоритма решения итоговой системы линейных алгебраических уравнений путем сравнения результатов решений квазистатической задачи о деформировании трубопровода под действием внутреннего давления и свободной внешней поверхности с известным аналитическим решением для задачи Ляме [2]. Известно, что при указанных способах нагружения радиальные перемещения в длинной толстостенной трубе могут быть описаны уравнением (1):
![]() (1)
(1)
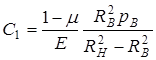 ,
, 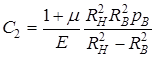
где ![]() – радиальные перемещения,
– радиальные перемещения, ![]() – внутренний радиус трубы,
– внутренний радиус трубы, ![]() – наружный радиус трубы,
– наружный радиус трубы, ![]() – внутреннее давление в трубе, E – модуль Юнга, µ – коэффициент Пуассона.
– внутреннее давление в трубе, E – модуль Юнга, µ – коэффициент Пуассона.
Определяется относительная погрешность численного решения:
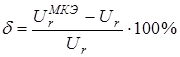 ,
,
где ![]() – радиальные перемещения, определенные численно.
– радиальные перемещения, определенные численно.
В таблице 1 представлена погрешность численного решения в зависимости от степени дискретизации рассматриваемой модели. Показано, что получаемые численные результаты сходятся к точному решению при увеличении числа узловых неизвестных, предложенная КЭ-модель корректна.
Таблица 1
Сходимость решений для квазистатической модели
|
№ |
Количество узлов по толщине, Nr |
Количество узлов по длине трубы, Nz |
|
|
δ, %*105 |
|
1 |
10 |
200 |
5.957454944219372 |
5.957770034843227 |
5.288 |
|
2 |
20 |
200 |
5.957650496822485 |
5.957770034843227 |
2.006 |
|
3 |
30 |
200 |
5.957697784551257 |
5.957770034843227 |
1.212 |
Второй тип проверки разработанной численной модели трубопровода основан на принципе Д’Аламбера, в соответствии с которым анализ динамической задачи может быть сведен к решению квазистатической задачи в которой учтены дополнительно силы инерции. Решается нестационарная задача о распространении волнового процесса вдоль стержня, возбужденного в результате приложения импульсного воздействия на одном из краю стержня, в котором известна теоретическая скорость распространения волны, зависящая от заданных параметров материала (рисунок 2). В предложенной динамической КЭ-модели для описания нестационарных процессов применяется конечно-разностная аппроксимация по времени. При известной теоретической скорости распространения волны и известной длине стержня определяется теоретическое время, за которое фронт волны распространится по всей длине стержня. Теоретическое время сравнивается с расчетным, определенным в результате численного эксперимента. Из условия близости теоретического и расчетного времен подбирается шаг по времени, дающий корректное решение динамической задачи, при котором правильным образом описываются инерционные силы, вычисляемые на основании глобальной матрицы масс в реализованном методе конечных элементов.
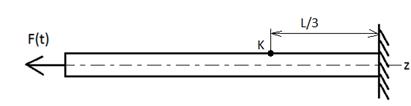
Рис. 2. Схема модельной задачи для определения дискретизации по времени
Анализ основных результатов
Реализованная конечно-элементная модель толстостенного трубопровода позволяет выполнять численное моделирование процесса распространения упругой волны в материале трубопровода при известных начальных и граничных условиях. На рисунке 3а показана форма импульса силы, прикладываемого к локализованной области на наружной поверхности трубопровода. Профиль нагрузки зависит от ряда параметров и может меняться с целью исследования динамического отклика системы на внешние воздействия различной частоты.
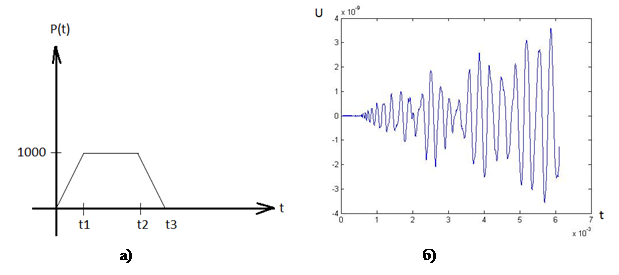
Рис. 3. Картина колебательного процесса в характерной точке трубопровода
На рисунке 3б показаны общие перемещения точки «K» на поверхности трубы, местоположение которой обозначено на рисунке 2.
На рисунке 4а отражено движение фронта волны по длине трубопровода в различные, но близкие моменты времени, вызванное приложением переменной силы на левом конце стержня (модельная задача, соответствующая схеме на рисунке 2), также представлена цветовая интерпретация волнового процесса, где разными цветами указаны различные амплитуды колебаний точек трубопровода: красная зона соответствует максимальным перемещениям точек среды в процессе вынужденных колебаний, синяя зона – нулевым смещениям точек трубопровода. Ширина цветной зоны зависит от периода действия силы на левом краю стержня. На рисунке наглядно видна локализованная в пространстве стержня область возмущенного движения, перемещающаяся с течением времени от левого края стержня к правому концу.
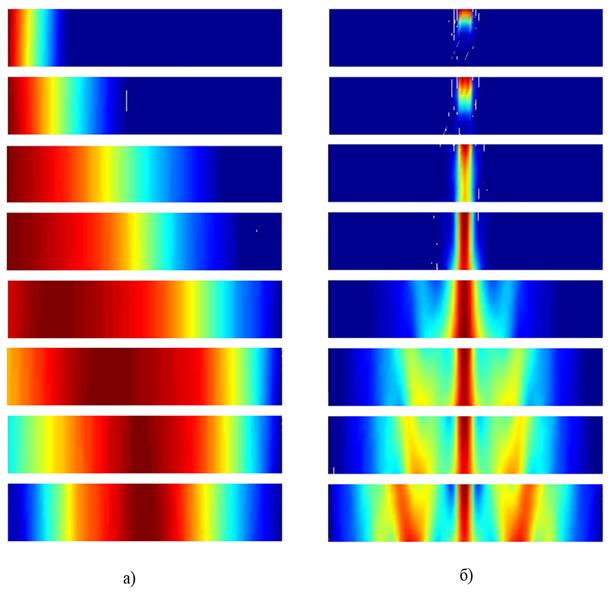
Рис. 4. Движение фронта волны при различных схемах нагружения
На рисунке 4б показано движение фронта волны во времени в случае, когда внешний импульс прикладывается в центре трубы на наружной поверхности перпендикулярно образующей трубы; в силу того, что задача решается в осесимметричной постановке, на рисунке отражена только лишь верхняя часть трубопровода, показанного на рисунке 1. На рисунке 4б наблюдаем волновой процесс, который сначала распространяется вдоль радиуса трубопровода. Затем фронт волны отражается от внутренней стенки трубы и направляется обратно вдоль радиуса к наружной поверхности и т.д. Однако в силу действия принципа Гюйгенса, в каждой точке среды, до которой дошел волновой процесс, возникают вторичные волны, начинающие распространяться влево и вправо под углом к оси трубопровода. На рисунке 4б можно наблюдать неоднократные отражения фронтов этих волн от стенок трубопровода.
Таким образом, разработанная численная динамическая модель трубопровода позволяет анализировать распространение вынужденных колебаний в материале рассматриваемого объекта, исследовать влияние геометрии объекта и вероятных локальных неоднородностей в виде трещин, мест локальных разрушений и пр. на картину волновых процессов [4].
На рисунке 3б показано сложное колебательное движение точки на поверхности трубопровода, включающее несколько гармоник. В настоящий момент предложена динамическая модель цилиндрического объекта, не учитывающая диссипативные свойства реального материала. В связи с этим, вынужденные колебания, показанные на графике 3б, являются незатухающими. После соответствующего усложнения рассматриваемой модели реакция системы на внешний импульс будет представлять собой ограниченные во времени затухающие колебания со сложным спектром, изменяющимся в зависимости от текущего состояния трубопровода, наличия в нем повреждений. Основные характеристики отклика системы на внешние воздействия могут быть получены в результате проведения гармонического анализа вынужденного движения некоторой точки в исследуемой области (представление колебательного движения в виде набора гармоник с известными амплитудами и частотами. Фурье-анализ).
Заключение
Для отработки методических подходов к реализации метода конечных элементов для динамических задач механики твердого деформируемого тела на более простых моделях на текущем этапе выполнения НИР задача решалась в осесимметричной постановке для однородной трубы без учета диссипативных свойств материала. Показаны возможные способы верификации конечно-элементной динамической модели для задачи механики деформированного твердого тела. Выполнена верификация разработанных численных моделей. Продемонстрированы возможности разработанной модели для визуализации волновых процессов в трубопроводе, изучения динамического отклика системы в характерных точках на внешние воздействия.
С помощью разработанной динамической параметрической конечно-элементной модели, описывающей волновые процессы, происходящие в трубопроводе под действием внешних возмущений, предлагается выполнить серию вычислительных многофакторных экспериментов с целью установления влияния локальных изменений в трубопроводе на спектр вынужденных колебаний в некоторой исследуемой точке.
По итогам исследования сформулирован подробный план дальнейших НИР:
1. Более качественное сравнение получаемых численных результатов с известными численными решениями. Уточнение необходимой степени дискретизации системы как по времени, так и по пространственным координатам.
2. Разработка диссипативных динамических моделей трубопроводов.
3. Учет влияния напряженного состояния, вызванного внутренним и внешним давлением, на характеристики колебательного процесса.
4. Переход от осесимметричной задачи к задаче в реальной трехмерной постановке.
5. Разработка математической и компьютерной моделей армированного трубопровода.
6. Адаптация программного кода в пакете MATLAB для использования эффективных встроенных алгоритмов и методов распределенных и параллельных вычислений. Проведение расчетов на высокопроизводительных вычислительных системах.
7. Проведение исследования для трубопровода, имеющего геометрические дефекты и локальные неоднородности. Подтверждение методами математического моделирования методики оценки остаточной работоспособности трубопроводов, основанной на данных вибродиагностики.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).
Рецензенты:
Шевелев Н.А., д.т.н., профессор кафедры «Динамика и прочность машин» ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Столбов В.Ю., д.т.н., профессор кафедры «Математическое моделирование систем и процессов» ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.



