Светоиндуцированная линза часто используется для исследования нелинейно-оптических свойств сред, а также в различных методах оптической диагностики материалов [1-8]. Наиболее детально разработан метод тепловой линзы, достаточно давно применяемый в термооптической спектрометрии [1-3]. Образованная лазерным пучком в среде линза увеличивает расходимость формирующего ее пучка (или пробного – в двухлучевой схеме), что регистрируется фотоприемником. Обычно в стандартной схеме тепловая задача рассчитывается при учете только радиального теплового потока, что применимо для толстой кюветы, когда поперечный размер луча много меньше длины (толщины) кюветы. Однако в ряде случаев возникает необходимость исследования тонкопленочных образцов. Такие задачи могут быть обусловлены, например, интегрально-оптическим исполнением экспериментальной схемы (с целью миниатюризации измерительной ячейки).
Цель исследования
В данной работе теоретически исследовано тепловое самовоздействие (термолинзовый отклик) гауссова пучка излучения в тонкослойной кювете.
Рассмотрим однолучевую схему измерения термолинзового сигнала (рис. 1). Пусть среда с коэффициентом поглощения 
находится в тонкой кювете толщиной 
. Для гауссова пучка распределение интенсивности падающего излучения в плоскости, перпендикулярной оптической оси z:
, (1)
где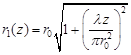 
– радиус пучка на расстоянии 
от перетяжки, r – расстояние от оси пучка, 
– длина волны излучения, 
– радиус пучка в перетяжке, 
– интенсивность излучения на оси в плоскости перетяжки пучка.
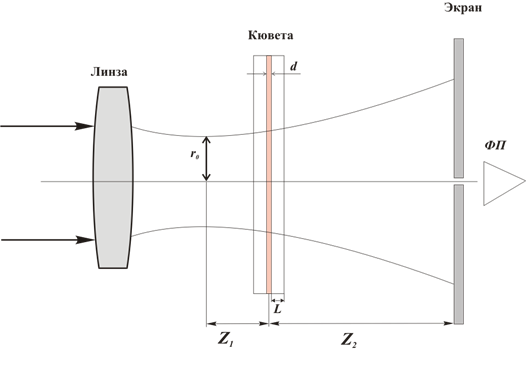
Рис. 1. К расчету термолинзового отклика среды в тонкослойной цилиндрической кювете (см. текст)
Термолинзовый сигнал определяется изменением приосевой интенсивности излучения за экраном
. (2)
Для нахождения параметров тепловой линзы рассмотрим тепловую задачу нагрева среды лазерным пучком. Считая, что для малых толщин слоя среды 
и окна кюветы 
(
) можно пренебречь радиальным (вдоль 
) тепловым потоком, получаем их одномерную тепловую задачу:
, (3)
где 
– удельные теплоемкость и плотность среды, 
– температура среды, 
– коэффициент теплопроводности среды.
Аналогично рассматривается тепловая задача для температуры в окне кюветы 
:
, (4)
где 
– теплофизические параметры материала окна.
Граничные условия на границе кювета-воздух соответствуют, например, конвективному теплообмену:
. (5)
где 
– соответственно коэффициент конвективного теплообмена и температура внешней среды, 
. На границе раздела среда кювета имеем условия равенства температур и тепловых потоков:
. (6)
. (7)
В стационарном режиме имеем следующие решения системы (3–7) для распределения температур в среде 
и окне кюветы 
:
, (8)
, (9)
. (10)
Для расчета термолинзового сигнала используем выражение для линзовой прозрачности кюветы [10]:
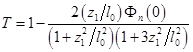(11)
(9)
где 
, 
– нелинейный набег фаз в оптической ячейке на оси пучка. Последний включает два вклада, обусловленных термолиной в слое среды и в окнах кюветы:
. (12)
, (13)
где 
и 
постоянные для нелинейной среды и материала окна соответственно.
Используя (9–11), получаем:
. (12)
(13)
Окончательно для стационарного термолинзового сигнала имеем выражение:
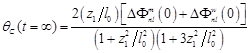. (14)
Полученное выражение показывает влияние на величину отклика как теплофизических параметров среды и материала кюветы, так и геометрических размеров оптической ячейки, жидкостью.
Выводы
В данной работе предлагается новая схема термолинзового эксперимента с тонкослойной кюветой, толщина которой значительно меньше размера светового пучка. В результате точного аналитического решения тепловой задачи в работе получено выражение для стационарного термолинзового отклика среды с учетом термолинзы в окнах кюветы. Применение данной схемы предпочтительнее для микрокювет с жидкофазными средами, поскольку в таких кюветах существенно ослаблено влияние конвекции на процесс измерения. Полученные результаты актуальны для нелинейной оптики дисперсных жидкофазных сред [6–9], а также для оптической диагностики таких сред (в т.ч. термооптической спектроскопии) [3].
Рецензенты:
Крылов В.И., д.ф.-м.н., профессор кафедры «Физика» ФГБОУ ВПО Дальневосточный государственный гуманитарный университет, г. Хабаровск;
Жуков Е.А., д.ф.-м.н., профессор кафедры «Электроника и электротехника» ФГБОУ ВПО Тихоокеанский государственный университет, г. Хабаровск.