В работе [1] предлагается способ повышения эффективности системы охлаждения трансформатора, основанный на барботировании масла инертным газом. В качестве инертного газа предлагается использовать элегаз, который характеризуется большим коэффициентом теплового расширения и большой плотностью. Большое значение коэффициента теплового расширения элегаза способствует образованию конвективных потоков, перераспределяющих неоднородности теплового поля в объеме трансформаторного масла.
В среде с конвективными ячейками возникает сложное поле скоростей, которое приводит к возрастанию эффективного коэффициента теплопроводности [2-4].
Предположим, что пузырьки имеют строго сферическую форму и жидкость, условно разделена на слои. Процесс теплообмена между слоями происходит быстрее, чем перенос вдоль оси Ох в отдельном слое. При наличии вплывающих пузырьков слои смещаются друг относительно друга. В начальный момент нижний слой начинает раздвигаться [5-6].
При дальнейшем всплывании пузырька слои смещаются друг относительно друга.
Максимальное смещение слоя происходит при нахождении слоя на уровне центра пузырька. В результате происходит перенос тепла, вдоль оси Ох. Такой процесс переноса тепла называется трансцилляторным.
Вычисление коэффициента трансцилляторного переноса, в основу которого положена редукция уравнения конвективной теплопроводности с переменными коэффициентами к эквивалентному интегро-дифференциальному уравнению с последующим интегрированием потока по времени и пространству, произведено в работе [3].
Соответствующее интегро-дифференциальное уравнение для температуры 
, позволяющее выразить температурное поле через градиент, представится как
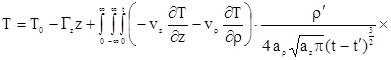
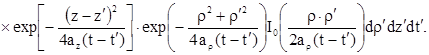
Представим всплывающий газ как правильно чередующиеся цепочки равноудаленных пузырьков с расстоянием 
между ними в цепочках. Полагаем, что пузырьки принимают сферическую форму и одинаковы по размерам, и радиусы всплывающих пузырьков намного меньше расстояний между ними, т.е. 
Это условие введено для того, чтобы поле скоростей в цепочке пузырьков можно было определить как сумму скоростей, создаваемых отдельными пузырьками. Скорость каждого пузырька постоянна, равна 
и направлена параллельно оси 
.
В нулевом приближении скорость газовой фазы внутри пузырька будем считать равной средней скорости, т.е. 
. Для нахождения поля скоростей жидкости при движении в ней бесконечной цепочки пузырьков газа воспользуемся принципом суперпозиции. Координаты вектора скорости для всплывающей цепочки пузырьков имеют вид бегущей волны
,
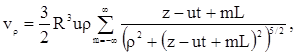
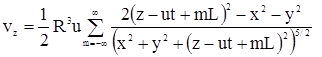где 
.
В случае пузырьков малых размеров и небольших объемных содержаний газовой фазы вкладом поля скоростей внутри пузырьков можно пренебречь. Для плоской упругой поперечной волны, распространяющейся вдоль оси 
, с плоскостью колебаний, параллельной оси 
, имеем:
(1)
Тогда выражение для коэффициента трансцилляторного теплопереноса имеет вид
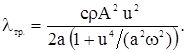(2)
При малых числах Маха 
разложим (2) в степенной ряд и, удерживая два члена, получим
.
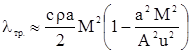Впрочем, при всплывании пузырьков в жидкости числа Маха, как показывают оценки, могут принимать значения порядка единицы и выше. Рассмотрим далее случай плоской немонохроматической волны, бегущей вдоль оси 
. Представив соответствующую координату скорости смещения среды в виде интеграла Фурье, получим
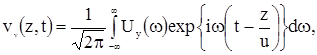(3)
где 
– спектральная компонента скорости. Для заданных коэффициентов Фурье смещений 
и 
в волновом поле имеем
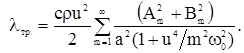(4)
Полученное выражение свидетельствует об аддитивности коэффициента трансцилляторного переноса 
относительно гармоник Фурье. Для монохроматических колебаний 
и 
(при 
),
из (4) получим выражение, совпадающее с (2). Поле скоростей в горизонтальном направлении представляет периодическую структуру типа стоячей волны, поэтому в нулевом приближении составляющую скорости запишем в виде 
, где 
. Точное решение отыскивается в виде
(5)
Параметры 
находим подстановкой 
в уравнение. Получим
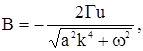(6)
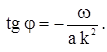(6а)
Таким образом, получим решение в следующем виде
(7)
В невозмущенном решении, плотность потока тепла
(8)
В точном решении, очевидно, средний по времени поток по прежнему направлен по оси . Усредняя полный поток и умножая на осредненную величину градиента температуры, получим выражение для определения эффективного коэффициента теплопроводности согласно диссипативной теореме Зельдовича
(9)
Поскольку
(9а)
(9б)
(9в)
. (9г)
Усреднение значения 
производится как по времени, так и по объему, в данном случае по . Найдем
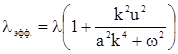. (10)
Как видно из формулы (10), эффективный коэффициент трансцилляторного переноса зависит от волнового числа 
, скорости всплытия пузырьков 
, молекулярного коэффициента переноса 
и частоты 
. Сравнение с формулой (2) показывает, что зависимость 
от , 
, и остается той же самой. Однако величина коэффициента в стоячей волне в два раза больше, чем в бегущей. Как не трудно убедиться, остальные зависимости для немонохроматических возмущений в стоячей волне получаются теми же, что и для бегущей волны.
Итак, конвективный перенос тепла в поле скоростей всплывающих пузырьков может быть представлен в виде потока, эквивалентного молекулярному. Это является следствием замкнутости потока, поскольку средний конвективный массоперенос за характерный период колебаний равен нулю. Аналогично легко показать, что конвективный теплоперенос в любых ячейках типа естественной конвекции эквивалентен молекулярному тепловому движению при условии замкнутости потока.
Заключение
Предложенная теория позволяет рассчитывать коэффициенты теплопереноса при «барботаже» жидкости газовыми пузырьками. Это открывает новые направления исследований в нефтехимической промышленности [2-4], тепло- и электроэнергетике.
Рецензенты:
Жирнов Б. С., д.т.н., профессор, заведующий кафедрой химико-технологических процессов филиала ФГБОУ ВПО УГНТУ, г. Салават;
Вильданов Р. Г., д.т.н., профессор кафедры «Электрооборудование и автоматика промышленных предприятий» филиала ФГБОУ ВПО УГНТУ, г. Салават.