Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Современная вычислительная техника в своем развитии ориентируется на аппаратные платформы с параллельной архитектурой. Эффективное применение таких вычислителей требует разработки специальных алгоритмов, учитывающих параллелизм выбранной аппаратной платформы. Одним из известных примеров таких алгоритмов являются параллельные методы решения задачи Коши. Различные варианты подобных методов приводятся в работах [2,3,4,5], при этом в каждом случае авторы применяют собственную оценку полученных решений, что затрудняет их сравнительный анализ.

Традиционным критерием вычислительной эффективности методов численного интегрирования (ЧМИ) обыкновенных дифференциальных уравнений (ОДУ) служит общее число арифметических операций на шаге интегрирования, необходимое для достижения требуемой точности решателя. Однако подобный подход учитывает лишь суммарное количество вычислений, вне зависимости от того, какие из них могут быть выполнены одновременно, а какие − строго последовательно. Это делает актуальной задачу оценки вычислительной эффективности решателя ОДУ с точки зрения параллельной организации процесса моделирования. Широко известный закон Амдала здесь обладает рядом недостатков, не учитывая, к примеру, неравномерность распределения действий в параллельных ветвях вычислительного процесса, что существенно при аппаратной реализации решателя.

В работе изложен авторский способ оценки вычислительной эффективности решателей ОДУ с учетом степени их собственного параллелизма. Приводятся примеры оценки различных решателей ОДУ с параллельной архитектурой. Компьютерное моделирование и автоматизированный расчет критерия реализованы в среде NILabVIEW.

Оценка вычислительных затрат решателя

Рассмотрим решатель ОДУ, в котором некоторый объем действий должен быть выполнен строго последовательно, а другая часть вычислений может быть распараллелена. Определим совокупность параметров, характеризующих вычислительную эффективность такого решателя. Пусть − общее число арифметических операций решателя ОДУ на одном шаге, а − объем вычислений, который можно распределить между вычислительными процессорами, при этом число арифметических операций на каждом из них составит . В качестве оценки вычислительных затрат решателя (ОВЗАР) будем рассматривать сумму действий нераспараллеливаемой части и приведенное число вычислений, содержащееся в параллелизуемой части решателя:

. (1)

Приведенное число действий в параллельной части решателя зависит от распределения общего объема вычисленийна параллельных вычислительных процессоров. Ключевыми параметрами такого распределения являются последовательность, содержащая наибольшее число арифметических операций в распараллеленной части процесса, и соотношение между длиной этой последовательности и числом операций при теоретически оптимальном распределении действий между процессорами . Второй параметр отражает равномерность распределения вычислений в распараллеленной части решателя при использовании заданного числа вычислительных процессоров с длиной максимальной цепочки арифметических операций . Для оценки данного параметра введем критерий эффективности параллелизма (КЭП) :

. (2)

Для того чтобы проиллюстрировать принцип работы КЭП, рассмотрим три примера распараллеливания вычислительного процесса, содержащего 8 операций (рис. 1).

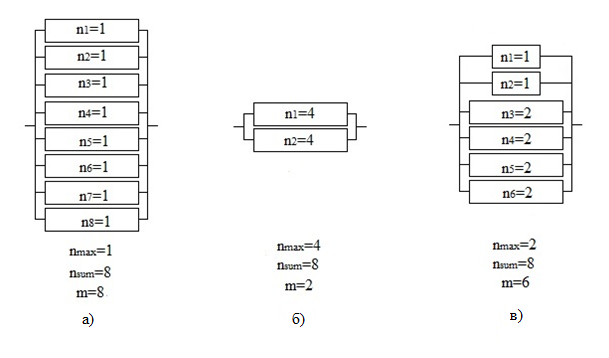
Рис. 1. Способы организации параллельного вычислительного процесса, содержащего 8 операций

Наибольшее ускорение вычислений будет достигнуто на 8 вычислительных процессорах, каждый из которых выполнит одно действие (рис. 1,a). Третий способ распараллеливания (рис. 1,в) даст нам худшую сбалансированность, чем другие два способа, но максимальная цепочка последовательных арифметических операций в этом случае будет короче, чем в случае (рис. 1,б) с двумя вычислительными процессорами. Вычислим значение КЭП для рассматриваемых случаев:

(3)

(4)

(5)

Полученные значения КЭП подтверждают сделанные предположения. Наблюдается следующая тенденция: при увеличении числа вычислителей или степени неравномерности распределения арифметических операций на параллельных вычислителях значение КЭП увеличивается. При этом значения КЭП лежат в интервале:

(6)

Вернемся к первоначальной задаче, составив выражение для приведенного числа действий распараллеленной части решателя с учетом КЭП. Поскольку значение КЭП при ухудшении качества реализации параллельной части решателя стремится к своей правой границе, то наибольшее ускорение вычислений будет достигаться при минимальной разности этих двух величин. Таким образом, приведенное число действий распараллеленной части решателя можно выразить как:

(7)

Данный подход к оценке вычислительной эффективности решателей ОДУ позволяет сравнивать между собой решатели, опирающиеся на численные методы одного порядка алгебраической точности.

Приведем примеры расчета ОВЗАР и КЭП для нескольких решателей, основанных на известных численных методах интегрирования.

Рассмотрим задачу Коши:

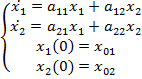(8)

Построим решатель, моделирующий систему (8) методом Рунге – Кутты второго порядка (РК2). Блок-диаграмма решателя представлена на рисунке 2.

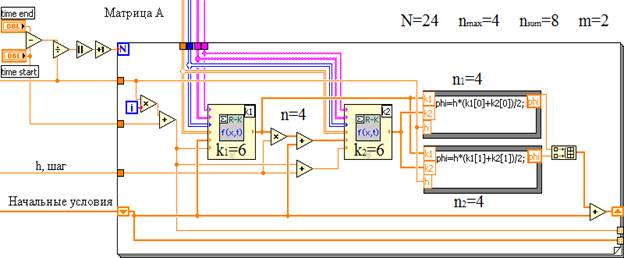
Рис. 2. Блок-диаграмма решателя ОДУ на основе метода РК2

Число арифметических операций N на шаге составит, из которых 8 выполняются в распараллеленной части решателя на вычислительных процессорах. Длина последовательности, содержащей наибольшее число арифметических операций равна 4. Применим формулы (2) и (7) для вычисления КЭП и приведенного числа действий распараллеленной части рассматриваемого решателя. Значение КЭП составит , а число приведенных действий. Тогда ОВЗАР по формуле (1) будет равна .

Рассмотрим решение этой же системы параллельным численным методом интегрирования второго порядка Д2, подробно описанном в работе [2]. Блок-диаграмма решателя, реализующего метод Д2, представлена на рисунке 3.

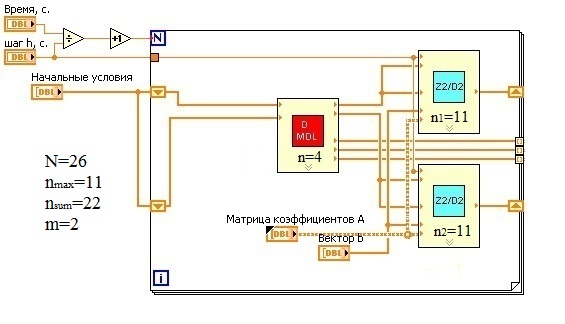
Рис. 3. Решатель на основе параллельного метода Д2

Число арифметических операций на шаге составит 26, из которых 22 выполняются в распараллеленной части решателя на двух вычислительных процессорах. Длина последовательности, содержащей наибольшее число арифметических операций, составляет 11. Используя формулы (2) и (7), вычислим значение КЭП и приведенное число действий распараллеленной части решателя. Таким образом, ОВЗАР для решателя методам Д второго порядка равна.

Можно предположить, что для разных решателей ОДУ значение ОВЗАР по-разному изменяется с ростом порядка моделируемой системы. Для проверки данного предположения была проведена серия компьютерных экспериментов в среде LabVIEW. Рассматривались линейные стационарные однородные системы с полностью заполненной матрицей коэффициентов размерностью от 2 до 5. Привести полностью блок-диаграммы всех проанализированных решателей не представляется возможным в связи с ограничениями на объем статьи. Результаты соответствующих экспериментов для решателей, использующих метод РК2 и параллельный метод Д2, сведены в табл. 1. Представлены рассчитанные параметры, использовавшиеся при оценке решателей.

Таблица 1

Изменение ОВЗАР с ростом порядка матрицы коэффициентов

Построим графики зависимости ОВЗАР рассматриваемых методов РК2 и Д2 от порядка матрицы коэффициентов моделируемой системы (рис. 4). В качестве эталона используем число действий на одном шаге интегрирования для явного метода Эйлера первого порядка точности (Forward Euler), как имеющего наименьшие вычислительные затраты среди всех известных численных методов интегрирования ОДУ.

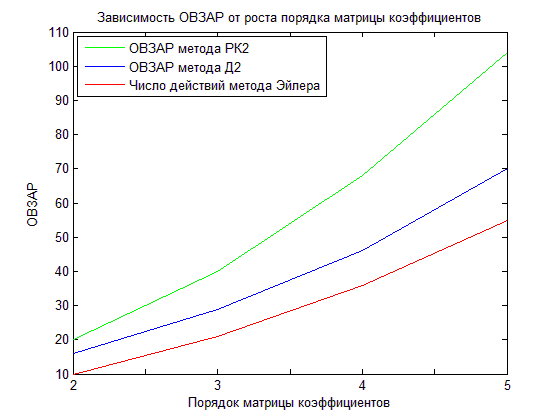
Рис. 4. Зависимость ОВЗАР методов Д2 и РК2 от порядка матрицы коэффициентов моделируемой системы уравнений

Из представленного на рисунке 4 графика видно, что вычислительные затраты метода Д2 растут существенно медленнее, чем у метода РК2, и темпы их роста сопоставимы с таковыми для метода Эйлера. Также можно предположить, что с увеличением порядка системы вычислительная эффективность методов Д будет возрастать быстрее относительно классических методов Рунге – Кутты.

Заключение

Предложенный способ оценки вычислительных затрат решателей обыкновенных дифференциальных уравнений представляет собой эффективный инструмент при анализе подобных алгоритмов с точки зрения вычислительного параллелизма. Применение данного подхода позволяет свести выбор решателя для конкретной задачи Коши к сравнению простых количественных характеристик – коэффициентов ОВЗАР. Это дает возможность разработчикам параллельных численных методов объективно оценивать и сравнивать полученные решения.

Проведенный в статье анализ зависимости вычислительной эффективности различных решателей от порядка моделируемой системы позволяет сделать выводы о том, что рассматриваемый в статье [2] параллельный метод интегрирования ОДУ второго порядка имеет лучшие вычислительные свойства по сравнению с классическими явными методами Рунге – Кутты при таком же порядке алгебраической точности.

Полученные результаты могут быть эффективно использованы при разработке аппаратных решателей ОДУ с параллельной архитектурой, а также цифровых систем управления и обработки сигналов на базе таких решателей.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках договора № НК 14-01-31277\14 от 06.02.2014 г.

Рецензенты:

Авдеев Б.Я., д.т.н., профессор кафедры информационно-измерительных систем и технологий, ФГАОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург;

Анисимов В.И., д.т.н., профессор кафедры систем автоматизированного проектирования, ФГАОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.