Робастный подход синтеза управления подразумевает построение алгоритмов, нечувствительных, «грубых» к различного рода неопределенностям. Ввиду определенной размытости термина «робастность», к системам данного класса будем относить системы с релейным типом управления и настройки, в том числе системы с переменной структурой. Функционирование последних связано с организацией движения по назначенным многообразиям скольжения, которое нечувствительно или робастно к неопределенностям различной природы.
Синтез робастного управления
Рассмотрим уравнения динамики манипуляционного робота (МР) [1, 3, 4]:
, (1)
где q – n-мерный вектор обобщенных координат МР;
D(q) – матрица инерции,
матрица, определяющая вектор центробежных и кориолисовых сил;
G(q) – вектор статических сил / моментов, действующих на манипулятор;
F(q) - вектор сил / моментов сопротивления;
u – вектор управляющих сил / моментов, создаваемых исполнительными двигателями манипуляционного робота.
Введем векторную переменную
, (2)
где вектор-функция v будет выбрана позже. Следует заметить, что при выборе 
вектор 
имеет смысл рассогласования между фактическим и желаемым значениями обобщенных координат робота; при выборе 
вектор описывает поверхность скольжения и т.д.
Из определения s очевидно, что
(3)
и, следовательно,
. (4)
В этом случае уравнение динамики может быть переписано в следующем виде:
. (5)
Далее воспользуемся следующим свойством уравнений динамики манипуляционных роботов: указанные уравнения, как и уравнения динамики МР, всегда можно параметризовать, т. е. записать в линейной форме относительно параметров манипулятора или их комбинаций.
Итак, в силу отмеченного свойства левая часть уравнений динамики манипуляционного робота (без учета сил и моментов вязкого сопротивления ) представима в виде
, (6)
где
–
надлежащим образом выбранный m-мерный вектор параметров манипулятора или их комбинаций, 
так называемая матрица-регрессор, структура которой известна и которая не содержит параметров манипулятора. Размерность матрицы 
равна 
.
С учетом параметризации (6) уравнения динамики МР примут следующий вид:
. (7)
Выберем теперь закон управления в виде[2]:
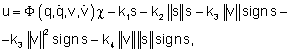(8)
где
,
а функция c должна быть далее выбрана надлежащим образом.
Из уравнения (7) выразим слагаемое 
:
. (9)
При выбранном виде закона управления (8) соотношение (9) преобразуется к следующему:
(10)
Выберем функцию Ляпунова в виде
. (11)
(напомним, что матрица инерции D(q) является положительно-определенной).
Полная производная функции Ляпунова по времени вдоль траектории системы вычисляется как
.
Заменяя слагаемое в соответствии с выражением (10), приходим к следующему виду производной функции Ляпунова:
(12)
В выражении для 
имеется слагаемое вида
в силу известного свойства кососимметричности матрицы 
–2C.
Теперь выполним оценку слагаемого 
в выражении для производной функции Ляпунова. Из (3) следует, что
Далее для синтеза управления будут необходимы оценки вектора 
.
Анализ математических моделей [2] показывает, что силы и моменты сопротивления, действующие на МР (с учетом ограничений на координаты), с высокой степенью точности можно аппроксимировать следующим аналитическим соотношением:
, (13)
где 
– ограниченные коэффициенты.
Оценим норму вектора
.
Из приведенного выражения (13) следует неравенство:
для 
Из очевидного условия
следует оценка нормы вектора сил / моментов вязкого сопротивления:
, (14)
где 
,
–
положительные константы.
Теперь для оценки производной функции Ляпунова имеем следующие неравенство:
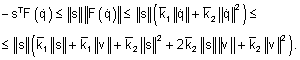(15)
Заменяя в соотношении (12) слагаемое – 
полученной мажорирующей функцией (15), приходим к следующему неравенству:
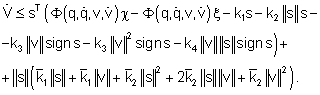(16)
После преобразования неравенство принимает вид, более удобный для анализа:
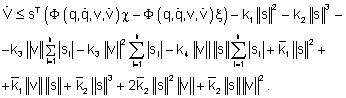(17)
Выберем теперь коэффициенты в выражении закона управления (17) таким образом, чтобы обеспечить отрицательность производной функции Ляпунова. Положим, что
, 
, 
, 
, 
.
(18)
С учетом очевидного неравенства
нетрудно убедиться в том, что выбранные значения коэффициентов закона управления (8) обеспечивают отрицательность полной производной по времени функции Ляпунова и, следовательно, асимптотическую устойчивость системы управления робота. Изображающая точка системы, возможно за конечное время, попадает на многообразие s = 0, которое определяет финальную часть процессов в системе управления[5]. В свою очередь, само многообразие s = 0 определяется выбором функции 
в выражении (2). Удобство настоящего подхода заключается в том, что собственно выбор функции может быть сделан практически независимо от других этапов синтеза. Надлежащим выбором функции (не обязательно в линейном виде) обеспечивается асимптотическое стремление обобщенных координат МР qi к желаемым программным значениям.
Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.
Рецензенты:
Завьялов В.В., д.т.н., профессор, профессор кафедры Технических средств судовождения, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток;
Глушков С.В., д.т.н., профессор, заведующий кафедрой Автоматических и информационных систем, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток.