Важным моментом в этом процессе является учет сезонной волатильности, поскольку существует достаточно большое множество категорий товаров и услуг, цены на которые подвержены сезонным колебаниям. Так, хорошо известны сезонные особенности цен на рынке жилой недвижимости. В зависимости от времени года изменяются цены на сельскохозяйственную продукцию, одежду, обувь, автомобили, лекарственные средства, алкогольную продукцию, драгоценные металлы, нефть, туристические услуги, железнодорожные и авиабилеты и т.д. Периодические колебания цен могут возникать и на более длительных временных интервалах.
Целью данной работы является исследование нелинейной модели динамики цены, которая сводится к уравнению Риккера [3], возникшее в математической биологии для описания динамики численности популяции.
Идея применения биологических моделей в экономике представляется перспективной, шаги в этом направлении были предприняты, например, в работах [3,5,7].
Опишем динамику цены уравнением [3]
,(1)
где 
–
параметр адаптации, характеризующий
скорость реакции цены на дисбаланс рынка, 
и
объемы спроса и предложения в период 
.
Пусть объемы спроса и предложения выражаются формулами:
,(2)
,(3)
тогда уравнение (1) имеет вид
(4)
Произведя замены
, 
,
приходим к
уравнению Риккера [6]:
(5)
Изменение динамического поведения модели (5) в зависимости от параметра достаточно хорошо изучено. Так, например, проведен анализ динамического поведения модели при учете колебаний параметра, характеризующего степень экологического лимитирования роста численности [2], подробно исследована задача оптимизации промысловых изъятий из риккеровских популяций при условии циклического изменения параметров [1,4].
В данной работе исследуется динамика цены,
описываемая уравнением (5), при периодическом изменении параметра 
в цикле длины два. Предположим, что
параметр изменяется периодически под
влиянием сезонных изменений свободных переменных 
и
в формулах спроса и предложения.
Учитывая указанные условия, получим модель динамики цены, описываемую следующей системой уравнений:
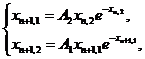(6)
где 
.
Или
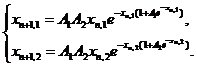(7)
В связи с симметричностью уравнений системы относительно параметров, рассмотрим одно из уравнений, например,
(8)
Стационарные
точки 
находим из уравнения
(9)
или 
.
Вопрос
об устойчивости равновесных значений рассматривается методом исследования
производной правой части (9). Положение равновесия является локально устойчивым
в случае, когда отклонения, возможно достаточно малые, от этого положения с
течением времени убывают, и неустойчивыми, когда эти отклонения возрастают. Для
гладкой функции 
используем следующий
критерий устойчивости неподвижной точки 
уравнения
: неподвижная точка устойчива, если 
, и неустойчива, если 
.
Таким
образом, в области 
, имеем единственную
неподвижную точку , являющуюся глобально
устойчивым положением равновесия.
При
нулевое положение равновесия
неустойчиво. Характер устойчивости нетривиальной неподвижной точки уравнения (8),
для которого 
, можно определить из решения
соответствующих неравенств.
1)
В случае если 
, неподвижная
точка устойчивая, переход к
равновесию происходит монотонно.
2)
Если 
, то неподвижная
точка устойчивая, переход к
равновесию происходит путем затухающих колебаний.
3)
Если 
, то неподвижная
точка неустойчивая, отход от которой
происходит путем расходящихся колебаний.
4)
В случае если 
неподвижная
точка неустойчивая, отход от которой
осуществляется монотонно.
Для
нетривиальной неподвижной точки ,
удовлетворяющей уравнению (9) производная имеет вид 
.
Отметим
следующие результаты аналитических исследований устойчивости нетривиальной
неподвижной точки в области .
При 
-
устойчивая, более того, переход к равновесию происходит монотонно, причем 
.
Если 
, то -
устойчивая неподвижная точка, переход к равновесию происходит монотонно при 
и путем затухающих колебаний при 
.
Если 
, то -
устойчивое состояние переход к равновесию происходит монотонно при 
.
Если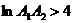 
, то при выполнении условия 
, нетривиальное стационарное состояние
является устойчивым с монотонным переходом.
Численные методы позволяют сделать выводы о наличие циклов и характере их устойчивости. Бифуркационные диаграммы, построенные для каждого периода в трехмерном пространстве в зависимости от параметров, а также сечения бифуркационной диаграммы плоскостями постоянных значений одного из параметров, иллюстрируют влияние параметров спроса, предложения и адаптации на сезонное изменение динамики цены. Анализ бифуркационных диаграмм, классификация их сечений требуют дополнительных исследований, подробное описание которых предполагается изложить в следующих работах по предложенной теме.
Сделанные на основании полученных результатов численных и аналитических исследований выводы имеют определенный экономический интерес и могут быть использованы при изучении динамики цены, описываемой предложенной моделью.
Рецензенты:Солодухин К.С., д.э.н., профессор, профессор кафедры математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток;
Мазелис Л.С., д.э.н., заведующий кафедрой математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток.