В то же время любая машина, в которой имеются вращающиеся массы, генерирует вибрацию периодического характера, повторяющуюся через определенный промежуток времени. Регистрируя вибрации, можно обнаружить поверхностные и внутренние дефекты и повреждения, возникающие в элементах машины. Этот принцип лежит в основе вибродиагностики, позволяющей снизить затраты на обслуживание оборудования и уменьшить число отказов, приводящих его к неработоспособным состояниям.
Для примера приведем условную схему точек измерения параметров вибрации колесных блоков (рис. 1), где БП ПЗК – буксовый подшипник со стороны, противоположной зубчатому колесу, УЗК – узел зубчатого колеса, БП ЗК – буксовый подшипник со стороны зубчатого колеса, УМШ – узел малой шестерни. Таким образом, контроль технического состояния проводится по 4 признакам, для каждого из которых следует построить диагностическую модель.
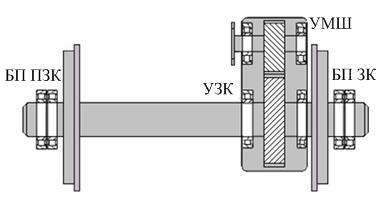
Рис. 1. Схема точек измерения параметров колесного блока
Модель диагностики
При описании процесса разрушения механических систем с помощью скрытой полумарковской модели (СПМ) мы можем оценить ненаблюдаемые состояния с использованием наблюдаемых сигналов датчиков. В качестве наблюдаемых данных выступает спектральная информация, полученная от колесных блоков в данной контрольной точке.
СПМ можно использовать для анализа собранных данных от скрытого источника диагностирования. Кроме того, СПМ можно обучить распознавать по данным измерений состояния сложного технического объекта, т.е. различные состояния скрытых компонентов по наблюдаемым значениям параметров[1]. Полностью обученная СПМ может рассматриваться как автомат, в котором каждое состояние представляет собой отдельное состояние диагностируемого объекта[2,3]. Переход между состояниями носит вероятностный характер, поэтому если диагностируемый компонент в момент времени t находится в состоянии si, можно предсказать, в каком состоянии он будет в момент времени t+1.
Общие предположения о модели в контексте задачи распознавания образов применительно к диагностированию состояния объекта диагностики (ОД) имеют следующий вид:
· следующее состояние зависит только от предыдущего состояния;
· наблюдаемое состояние в момент времени t зависит только от текущего состояния и не зависит от предыдущих наблюдений и состояний.
Полное описание СПМ λ предполагает задание:
-
матрицы переходов между состояниями моделиA =
{aij}, ![]() ,
,![]() ,
где N - количество состояний модели;
,
где N - количество состояний модели;
-
наблюдаемой матрицы выходных сигналов, значения элементов которой не зависят от
времени B = {bjk}, ![]() ,
, ![]() ,
где M – диапазон наблюдаемых
значений, которые могут порождаться моделью;
,
где M – диапазон наблюдаемых
значений, которые могут порождаться моделью;
- матрицы начального распределения
вероятностей между состояниями моделиπ={πi},
![]()
- матрица вероятности
распределений длительности состояний D= {di(l)},
где ![]() , l
– длительность состояния,
, l
– длительность состояния, ![]() .
.
Таким образом, в общем виде описать СПМ можно в виде следующей формулы:
![]() (1)
(1)
Процесс диагностирования с использованием описанной выше модели (1) описывается следующим образом.
В каждой КТ (рис. 1) для всех диагностируемых дефектов строятся моделиλn, а также модель, описывающая бездефектное состояние для данной КТ. Затем происходит настройка параметров моделей на сигналах, полученных в КТ от ОД в данном состоянии. В результате будет построено N моделей λn, каждая из которых будет описывать одно из диагностируемых состояний. После окончания процесса настройки параметров моделей есть возможность определения текущего состояния объекта диагностики.
Таким образом, алгоритмы диагностирования на основе СПМ можно разделить на два вида: алгоритм настройки параметров для создания моделей, способных определить текущее состояние объекта диагностики и алгоритм определения текущего состояния.
Алгоритмнастройки параметров
Для решения задачи обучения модели не существует аналитического решения, однако оптимизировать параметры моделей можно итерационной процедурой алгоритма Баума – Уэлча [4]. Алгоритм работает в два этапа. На первом этапе происходит инициализация параметров СПМ случайнымизначениями. На втором этапе итеративный процесс оптимизирует параметры модели на основе информации, полученной в КТ от объекта диагностики в данном состоянии. На основе этой информации происходит переоценка параметров модели. Таким образом, после каждой итерации цикла переоценки получается модель, которая лучше соответствует данным, полученным от ОД в данном состоянии. Итерации продолжаются до достижения момента, когда улучшение параметров модели будетменьше, чем выбранное пороговое значение.
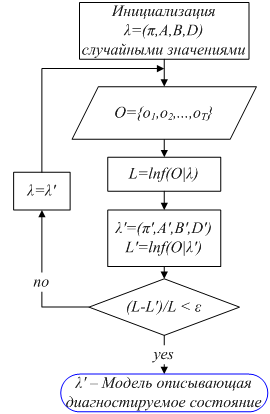
Рис. 2. Блок-схема алгоритма обучения СПМ
Расчет новых значений модели
![]() происходит
на основании вспомогательных переменных αt(i)и βt+d(j), которые вычисляются с помощью алгоритма
«прямого-обратного» хода [5].
происходит
на основании вспомогательных переменных αt(i)и βt+d(j), которые вычисляются с помощью алгоритма
«прямого-обратного» хода [5].
![]() ,
(2)
,
(2)
где![]() среднее значение вероятности
нахождения системы в состоянии i в
промежуток времени длительноси d и
затем перехода в состояние j:
среднее значение вероятности
нахождения системы в состоянии i в
промежуток времени длительноси d и
затем перехода в состояние j:
![]() (3)
(3)
![]() (4)
(4)
Улучшение параметров СПМ посредством итерационной процедуры Баума – Уэлча будем производить по следующим формулам.
1) начальное распределение вероятностей находитсякак вероятность того, что состояние i – начальное для данной последовательности:
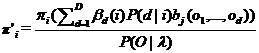 (5)
(5)
2)формула пересчета вероятностей перехода между состояниями системы рассчитывается как отношение ожидаемого числа переходов из состояния iв jк ожидаемому числу переходов из i:
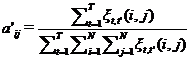 , (6)
, (6)
где ![]() –вероятность
нахождения системы в состоянии i – промежуток
времени длительностьюd, затем
перехода в состояние jдля данной
последовательности o1,o2,...,oT:
–вероятность
нахождения системы в состоянии i – промежуток
времени длительностьюd, затем
перехода в состояние jдля данной
последовательности o1,o2,...,oT:
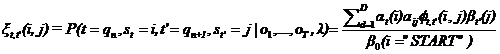 (7)
(7)
3) формула пересчета матрицы вероятностей наблюдений – это отношение ожидаемого количества наблюдений ot = vk в состоянии iк количеству всех наблюдений в состоянии i:
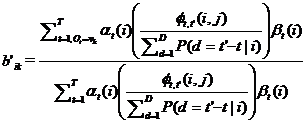 (8)
(8)
4) формула расчета для элементов матрицы распределений длительности состояний – это отношение ожидаемого числа состояний iдлительности dк ожидаемому числу состояний i:
 (9)
(9)
В качестве порогового значения для окончания процесса обучения выбрана величина изменения логарифмической функции правдоподобия. Таким образом, процесс обучения заканчивается на m-ом шаге при достижении следующего условия:
![]() , (10)
, (10)
где ε – заданная точность получения решения, представляющая малое положительное число, установленное опытным путем.
Алгоритм определения текущего состояния объекта диагностики
Идентификация текущего состояния данного вибросигнала реализуется как соревнование между моделями. Для всех моделей, описывающих состояния ОД в данной КТ, происходит расчет логарифмической функции правдоподобия. Модель с наибольшим значением логарифмической функции правдоподобия определяется как победитель и считается представителем текущего состояния объекта диагностики (рис. 3). Далее аналогичная операция производится для остальных КТ данного ОД. Диагнозом ОД считается сумма неисправностей,полученных от всех КТ. Полностью исправным ОД будет признан только в том случае, если для всех КТ победителем окажется модель λi, описывающая бездефектное состояние.
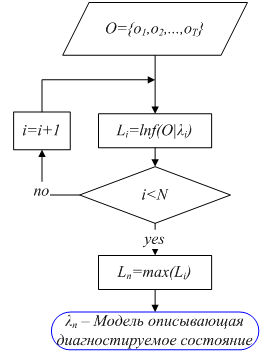
Рис. 3. Блок-схема алгоритма диагностирования
В статье описан вероятностный подход к построению диагностических систем. Предложенный метод реализован с использованием СПМ. Постановка диагноза осуществлялась на основе анализа вибросигналов, полученных от объекта диагностики. Использование данного метода позволяет автоматизировать процесс постановки диагноза и повысить точность постановки диагноза. Описанная модель диагностирования может служить основой для разработки методов прогнозирования технического состояния и перехода на обслуживание по фактическому состоянию.
Рецензенты:Моругин С.Л., д.т.н., профессор, профессор кафедры «Компьютерные технологии в проектировании и производстве», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.
МитяковС.Н., д.ф.-м. н., профессор, директор института экономики и управления, ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.



