Объективная метрика качества изображения является важной частью систем обработки изображений. Одним из важных применений объективных метрик оценки качества изображений является оценка эффективности алгоритмов и систем обработки изображений [1]. Несмотря на большое количество публикаций по данной тематике, задача оценки качества реконструированных изображений рассматривается лишь в немногих. В то же время задача восстановления утраченных областей изображения получила значительное внимание в последнее время [2, 3].
Возможны два подхода к оценке качества изображений: количественная оценка с помощью использования математических методов (среднеквадратическая ошибка, Lp-норма [4], меры, учитывающие особенности восприятия изображения зрительной системой человека) и субъективная оценка на основе экспертных оценок [5].
Оценка качества, полученная с использованием существующих подходов, может значительно отличаться от оценки, полученной с помощью людей-экспертов. Большинство существующих подходов для оценки качества используют эталонное изображение. Но, к сожалению, во многих случаях эталонное изображение недоступно. К таким задачам относится и задача реконструкции утраченных пикселей. Таким образом, задача разработки количественной метрики оценки качества реконструированных изображений является актуальной.
В разработке количественных оценок качества изображения достигнуты значительные успехи. Однако введенные критерии не являются достаточно совершенными. Большинство попыток найти приемлемые оценки качества изображения относится к частным случаям. Предлагается некая оценка, основанная на каких-либо физиологических предпосылках, а чаще просто удобная для анализа и вычислений, а затем оцениваются его свойства. Создание более совершенных оценок качества изображений связано с более глубоким изучением свойств зрительной системы человека.
Целью данной работы является разработка метрики оценки качества изображений при обработке методами реконструкции на основе машинного обучения.
Математическая модель
В статье используются обозначения, аналогичные обозначениям, принятым в работе [2]. Все изображение ![]() состоит из двух непересекающихся областей: реконструированной области
состоит из двух непересекающихся областей: реконструированной области ![]() , и известной области
, и известной области ![]()
![]() . На рисунке 1 показан пример расположения этих областей.
. На рисунке 1 показан пример расположения этих областей.
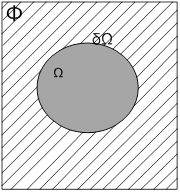
Рис 1. Модель изображения
Известно изображение ![]() и область Ω внутри его. Задача реконструкции состоит в модификации значений пикселей изображения внутри области Ω, таким образом, чтобы область не выделялась на фоне окружающего изображения [1]. Цель реконструкции может состоять в восстановлении поврежденных частей изображения (например, царапин и трещин на старых фотографиях) или удаления нежелательных объектов на изображении. Показанная на рисунке 1 область Ω всегда определяется пользователем, т.е. определение области Ω не является частью задачи реконструкции.
и область Ω внутри его. Задача реконструкции состоит в модификации значений пикселей изображения внутри области Ω, таким образом, чтобы область не выделялась на фоне окружающего изображения [1]. Цель реконструкции может состоять в восстановлении поврежденных частей изображения (например, царапин и трещин на старых фотографиях) или удаления нежелательных объектов на изображении. Показанная на рисунке 1 область Ω всегда определяется пользователем, т.е. определение области Ω не является частью задачи реконструкции.
Алгоритм оценки качества восстановления изображений
В общем случае для успешного построения метрики качества изображения на основе машинного обучения требуется решение трех следующих задач:
1. Определение пространства признаков ![]() , служащих описанием входных сигналов.
, служащих описанием входных сигналов.
2. Выбор функции отображения из пространства признаков в пространство оценок качества ![]() .
.
3. Обучение системы и проверка ее устойчивости (проверка на переобучение и т.д.).
Структурная схема выбранного подхода представлена на рисунке 2 и содержит следующие этапы:
1. Выбор области интереса (с использованием карты внимания);
2. Вычисление низкоуровневых признаков изображения;
3. Построение дескриптора восстановленной области на базе низкоуровневых особенностей;
4. Решение задачи регрессии с целью получения численной оценки качества на основе полученного вектора-дескриптора.
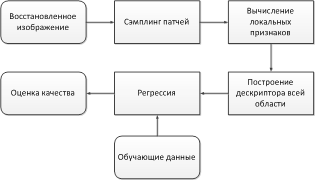
Рис. 2. Блок-схема алгоритма
В работе [5] показано, что визуальное внимание играет важную роль в зрительном восприятии человека. В каждый момент времени человеческий глаз ясно видит лишь небольшую часть сцены, в то же время гораздо более значительная область сцены воспринимается как «размытая». Этой «размытой информации» достаточно для оценки важности различных областей сцены и привлечения внимания к важным областям зрительного поля. Большинство методов позволяют получить карту внимания - двумерное изображение, в котором значения каждого пикселя связанно с важностью соответствующей области.
Для получения карт внимания используется Saliency Toolbox, описанный в работе [6]. Данный набор инструментов использует модель зрительной системы человека. Важно отметить, что нет смысла сравнивать восстановленную область на исходном и восстановленном изображении, так как общее содержание может значительно измениться. Для выбора областей интереса предлагается использовать следующее выражение:
![]() .
.
Здесь ![]() - карта внимания для реконструированного изображения, а
- карта внимания для реконструированного изображения, а ![]() значение карты внимания, соответствующее пикселю
значение карты внимания, соответствующее пикселю ![]() . В выражении, приведенном выше, плотность взгляда вычисляется внутри и снаружи восстановленной области изображений. Значение
. В выражении, приведенном выше, плотность взгляда вычисляется внутри и снаружи восстановленной области изображений. Значение ![]() используется в качестве порогового значения при принятии решения о том, какие части изображения будут использоваться при оценке, а какие нет. Принимаются во внимания только те области, для которых
используется в качестве порогового значения при принятии решения о том, какие части изображения будут использоваться при оценке, а какие нет. Принимаются во внимания только те области, для которых ![]() .
.
В качестве низкоуровневых признаков локальных областей используются спектральные представления. Далее предлагается анализ следующих базисов Фурье, Уолша, Хаара с использованием вектора эффективности. Для корректного вычисления составляющих системного критерия эффективности при наличии помех и искажений требует применения статистического усреднения.
При синтезе алгоритмов обработки сигналов и систем чаще всего используется критерий минимума среднего риска, позволяющий учесть статистику помех и сигналов. При реализации частотных преобразований и оценке вычислительных затрат существенное значение имеет выбор базиса спектрального разложения. Для оптимизации выбора базиса разложения сигналов целесообразно использовать критерий минимума среднего риска. Для этого необходимо, чтобы был задан класс используемых сигналов и процессов и были известны их вероятностные характеристики.
Для заданного класса двумерных процессов ![]() предполагается известной вероятность каждого из подклассов
предполагается известной вероятность каждого из подклассов![]() , где индекс
, где индекс ![]() – номер подкласса с некоторыми общими свойствами, а
– номер подкласса с некоторыми общими свойствами, а ![]() – номер реализации процесса
– номер реализации процесса ![]() –го подкласса. Будем сравнивать некоторую совокупность базисных систем
–го подкласса. Будем сравнивать некоторую совокупность базисных систем ![]() Разложение
Разложение ![]() в обобщенный ряд Фурье по
в обобщенный ряд Фурье по ![]() ,
,![]() -й базисной системе в общем виде имеет вид:
-й базисной системе в общем виде имеет вид: ![]() .
.
При конечном числе членов ряда Фурье можно охарактеризовать погрешностью: ![]() , где
, где ![]() – расстояние в некоторой метрике,
– расстояние в некоторой метрике, ![]() – частичная сумма
– частичная сумма ![]() членов ряда Фурье.
членов ряда Фурье.
Аппаратурное определение коэффициентов ряда Фурье или их вычисление связанно с определенными вычислительными затратами ![]() . Введем функцию потерь, учитывающую как потери, связанные с погрешностью усечения ряда Фурье, так и затраты аппаратурных и вычислительных ресурсов:
. Введем функцию потерь, учитывающую как потери, связанные с погрешностью усечения ряда Фурье, так и затраты аппаратурных и вычислительных ресурсов:
![]() .
.
Значение условного риска зависит как от подкласса сигналов, так и от базиса и вычисляется путем усреднения функции потерь по реализациям:
![]() ,
,
где ![]() – плотность вероятности анализируемых сигналов и помех; а угловые скобки означают операцию статистического усреднения.
– плотность вероятности анализируемых сигналов и помех; а угловые скобки означают операцию статистического усреднения.
Средний риск определяется путем усреднения условного риска по подклассам сигналов:
![]() ,
,
где ![]() – вероятность
– вероятность ![]() -го подкласса сигналов.
-го подкласса сигналов.
В соответствии с критерием минимума среднего риска из ![]() базисов выбирается тот, для которого средний риск минимален.
базисов выбирается тот, для которого средний риск минимален.
Для оценки эффективности системного критерия качества обработки изображений рассматриваются тестовые изображения в виде текстур, полученных на основе моделирования гауссовских полей с заданными корреляционными функциями. Генерирование однородных нормальных случайных полей, как и стационарных нормальных случайных процессов, наиболее просто производится методом формирующего фильтра [7].
В качестве примера в статье рассматривается представление случайных реализаций с различными корреляционными функциями в базисах тригонометрических функций (Фурье), Уолша и Хаара. Проведем анализ в выбранных базисах для созданных моделей изображений размером 256 на 256 пикселей. Зададимся также тремя типами распределения вероятностей подклассов: 1) равномерное: ![]() ; 2) убывающее:
; 2) убывающее: ![]() ;
;
3) возрастающее: ![]() . Выберем функцию стоимости в виде:
. Выберем функцию стоимости в виде: ![]() .
.
Средний риск определяется путем усреднения условного риска по подклассам сигналов с использованием принятых априорных вероятностей подклассов сигналов, рассчитанные значения представлены в таблице 1.
Таблица 1
Величины среднего риска
|
Базис |
Виды распределения вероятностей |
||
|
1 |
2 |
3 |
|
|
Фурье |
0,71 |
0,97 |
0,53 |
|
Уолша |
0,26 |
0,3 |
0,24 |
|
Хаара |
0,043 |
0,06 |
0,03 |
Результаты расчетов, представленные в таблице показывают, что для принятых моделей двумерных сигналов и распределений их вероятностей базис Хаара имеет наименьший средний риск, а базис Фурье наибольший.
На основе проведенного анализа выберем базис Хаара для представления локальных областей изображений. Следует отметить, что размер восстановленной области ![]() различен для различных изображений. В связи с этим на основе низкоуровневых признаков следует формировать высокоуровневое представление фиксированного размера. В качестве высокоуровневого представления используется подход «мешок слов». Процедура построения дескриптора (сигнатуры) восстановленной области состоит из двух шагов. На первом шаге строится словарь. Для этого используются низкоуровневые особенности, извлеченные из всех изображений обучающего набора изображений. Для построения словаря извлеченные особенности делятся на 100 классов с помощью алгоритма кластеризации k-средних. Каждый элемент словаря представляет собой центроид для одного из классов, найденных процедурой кластеризации. Каждое слово в словаре представляет преобразование Хаара в блоке изображения размером 8x8. Полученный словарь используется на втором этапе при построении гистограмм частот для слов из словаря в качестве вектора признаков – дескриптора восстановленной области (рис. 3). Полученный набор дескрипторов используется для обучения машины регрессии (Support Vector Regression). Для получения гистограммы частот слов из словаря извлекаются все визуально заметные области (заметность определяется с использованием карт внимания) конкретного изображения. Затем к каждому из извлеченных блоков применяется преобразование Хаара и выполняется классификация согласно полученному словарю на основе евклидова расстояния [8].
различен для различных изображений. В связи с этим на основе низкоуровневых признаков следует формировать высокоуровневое представление фиксированного размера. В качестве высокоуровневого представления используется подход «мешок слов». Процедура построения дескриптора (сигнатуры) восстановленной области состоит из двух шагов. На первом шаге строится словарь. Для этого используются низкоуровневые особенности, извлеченные из всех изображений обучающего набора изображений. Для построения словаря извлеченные особенности делятся на 100 классов с помощью алгоритма кластеризации k-средних. Каждый элемент словаря представляет собой центроид для одного из классов, найденных процедурой кластеризации. Каждое слово в словаре представляет преобразование Хаара в блоке изображения размером 8x8. Полученный словарь используется на втором этапе при построении гистограмм частот для слов из словаря в качестве вектора признаков – дескриптора восстановленной области (рис. 3). Полученный набор дескрипторов используется для обучения машины регрессии (Support Vector Regression). Для получения гистограммы частот слов из словаря извлекаются все визуально заметные области (заметность определяется с использованием карт внимания) конкретного изображения. Затем к каждому из извлеченных блоков применяется преобразование Хаара и выполняется классификация согласно полученному словарю на основе евклидова расстояния [8].
Каждый бин результирующей гистограммы содержит число низкоуровневых особенностей конкретного класса в данной восстановленной области. После нормализации гистограммы получается «сигнатура» изображения – высокоуровневое представление восстановленной области [8].
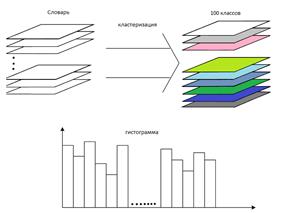
Рис.3. Построение гистограммы
Оценка эффективности алгоритма оценки качества восстановления изображений
С целью оценки эффективности разработанной метрики использовался набор тестовых изображений. Набор состоит из 300 изображений. В качестве методов восстановления выбраны следующие подходы: метод, основанный на поиске самоподобных областей, метод, основанный на спектральных преобразованиях, метод, основанный на вычислении частных производных. Для каждого изображения была получена экспертная оценка, с привлечением 30 человек. Результаты были разделены на два непересекающихся набора. Первый использовался для обучения, а второй для проверки результата.
Эксперты оценивали качество по шкале, в которой 5 соответствует «Отлично», а 1 – соответствует «Очень плохо». Для оценки эффективности полученной метрики используется коэффициент корреляции между векторами полученных с помощью объективной метрики и экспертным методом оценок качества. Анализ полученных результатов в таблице 2 показывает, что предложенный подход превосходит известные метрики качества на выбранном наборе тестовых данных.
Таблица 2
Коэффициент корреляции для различных методов вычисления объективной
метрики качества изображений
|
DN |
SSIM |
ASVS |
Предложенный подход |
|
0,854 |
0,768 |
0,834 |
0,892 |
Заключение
В статье представлена объективная метрика оценки качества изображений на основе машинного обучения. Количественные меры качества изображения необходимы для проектирования и оценки систем воспроизведения изображений. Эти меры во многом помогут избавиться от трудоемкой и неточной современной методики оценки изображений посредством субъективной экспертизы. Кроме того, на основе количественных мер можно развивать методы оптимизации систем обработки изображений. Продемонстрировано, что оценка качества, полученная с использованием приведенного подхода коррелирует с субъективной оценкой качества.
Работа поддержана Минобрнауки России в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы» (соглашение №14.586.21.0013).
Рецензенты:
Федосов В.П., д.т.н., профессор, заведующий кафедрой ТОР инженерно-технологической академии Южного Федерального Университета, г.Ростов-на-Дону;
Марчук В.И., д.т.н., профессор, заведующий кафедрой «Радиоэлектронные и электротехнические системы и комплексы» ИСОиП (филиал ДГТУ), г.Шахты.



