Явление локализации может быть охарактеризовано двумя уровнями. Первый - это слабая локализация или усиление обратного рассеяния, связанное с взаимной когерентностью волн, многократно рассеянных на одних и тех же элементах среды при распространении во взаимно противоположных направлениях. Второй - сильная локализация (далее локализация) - полное подавление распространения волн в сильно рассеивающей среде [1,4].
На сегодняшний день существуют два основных критерия наступления локализации электромагнитных волн:
1. Коэффициент прохождения волн через не поглощающую структуру приобретает экспоненциально убывающий характер, описываемый законом T ≈ exp(–L/lloc), где L – линейная протяженность среды, lloc – локализационная длина, являющаяся параметром, определяющим степень локализации излучения.
2. Критерий Иоффе – Регеля: k l ≤ 1, где k – волновое число, l – длина свободного пробега электромагнитной волны.
l=1/σ·n, (1)
где σ – поперечник рассеяния элементов среды, n - концентрация (количество элементов на единицу площади).
Теоретические исследования локализации волн в различных средах ведутся либо на основе строгих численных методов, либо приближенно, исходя из теории эффективной среды. В последнем случае становится возможным описать основные локализационные параметры достаточно простыми аналитическими выражениями. Для выявления локализационных состояний при численном моделировании процесса распространения lloc должна быть меньше линейных размеров исследуемой случайной структуры. При этом для получения малых значений удобно рассматривать локализационные эффекты в сильно рассеивающих средах. Такая ситуация возможна при рассмотрении резонансных случаев, например, обусловленных резонансами Ми для частиц, образующих дискретную структуру. Альтернативой может служить анализ систем, в которых рассеиватели имеют значительно больший показатель преломления, чем окружающая их однородная среда заполнения.
Целью данной работы является сравнительный анализ двух методик определения локализационной длины: на основе строгого численного метода и аналитического подхода.
Численное моделирование процесса.
Исследуемая структура представляла собой N круговых цилиндров радиуса a=0,05 мм, размещенных случайно и параллельно друг другу в однородной среде в пределах прямоугольной площадки длиной L=12 мм и шириной W = 90 мм, со средней плотностью ρ = 0.5 мм-2. Структура возбуждалась полем линейного электрического тока, ориентированного параллельно цилиндрам, таким образом, рассматривался случай Е поляризации волн (рис. 1).
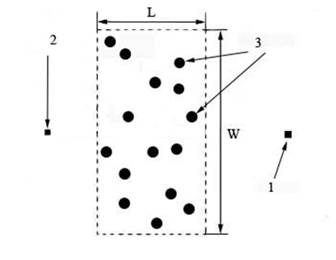
Рис.1. Концептуальная схема рассматриваемой в работе системы. 1 – источник поля, 2 – место расположение приемника излучения, 3 – цилиндрические рассеиватели.
Численное моделирование проводилось на основе теории многократного рассеяния [5]. Методика расчетов применительно к задачам рассеяния волн на системах цилиндрических элементов подробно обсуждалась в [2]. Кратко суть ее сводится к следующему.
Поле в присутствии системы параллельных цилиндров может быть представлено в виде:
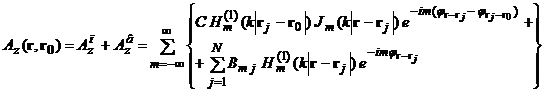 (2)
(2)
где
первое слагаемое описывает поле прямой волны, второе – поле, рассеянное на
цилиндрах; ![]() - функция Ханкеля первого рода
m-ого порядка, Jm –
функция Бесселя m-ого порядка; волновое число
- функция Ханкеля первого рода
m-ого порядка, Jm –
функция Бесселя m-ого порядка; волновое число ![]() , где с – скорость света, f – частота; r0, r,
rj – радиус-векторы,
определяющие положение источника, приемника поля и произвольного j-го цилиндра соответственно; φ – азимутальные углы, образованные
указанными векторами и осью x декартовой системы координат; С – коэффициент, описывающий амплитуду
падающей волны, Bm j
– коэффициенты, определяющие амплитуду возбуждения j-го цилиндра под действием поля прямой
волны и волн, рассеянных на других элементах структуры (рис. 2).
, где с – скорость света, f – частота; r0, r,
rj – радиус-векторы,
определяющие положение источника, приемника поля и произвольного j-го цилиндра соответственно; φ – азимутальные углы, образованные
указанными векторами и осью x декартовой системы координат; С – коэффициент, описывающий амплитуду
падающей волны, Bm j
– коэффициенты, определяющие амплитуду возбуждения j-го цилиндра под действием поля прямой
волны и волн, рассеянных на других элементах структуры (рис. 2).
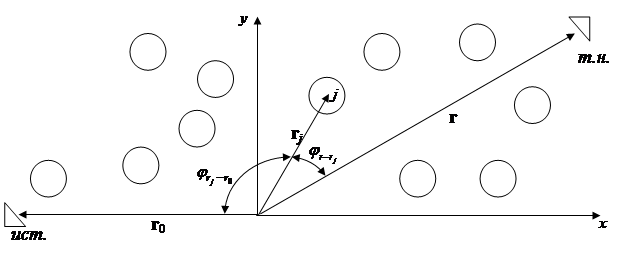
Рис. 2. Иллюстрация аргументов функций в формулах (2) и (3).
Для нахождения неизвестных коэффициентов необходимо удовлетворить граничным условиям на поверхности цилиндров. Для этого при формулировке данных условий на одном из элементов, волновые функции в дифракционных рядах, описывающих поля, рассеянные на остальных цилиндрах, с использованием теоремы сложения выражаются через собственные волновые функции рассматриваемого элемента. В результате выражение (2) приводится к виду:
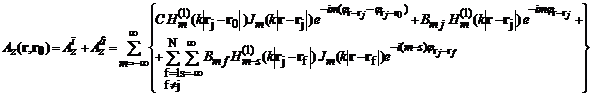 (3)
(3)
Последовательно
удовлетворяя граничным условиям на поверхности каждого рассеивателя, получаем
систему N линейных алгебраических уравнений относительно коэффициентов Bm,
которую решаем стандартными методами, определяя тем самым поле в присутствии
двумерной системы случайно расположенных элементов. В ходе численного
моделирования определялись значения полной ![]() и когерентной
и когерентной ![]() интенсивностей
излучения, нормированные интенсивностью поля в отсутствии структуры
интенсивностей
излучения, нормированные интенсивностью поля в отсутствии структуры ![]() ,
а также коэффициент прохождения волн сквозь структуру
,
а также коэффициент прохождения волн сквозь структуру ![]() . Знак
. Знак ![]() означает
усреднение по реализациям расположений элементов, число которых определялось
сходимостью результатов расчетов и варьировалось от 500 до 1000.
означает
усреднение по реализациям расположений элементов, число которых определялось
сходимостью результатов расчетов и варьировалось от 500 до 1000.
После вычисления вышеуказанных величин длина локализации волн в рассматриваемой системе определяется как:
lloc=-L/<ln |T|2> (4).
Аналитическое описание.
Анализ процесса рассеяния в рассматриваемых средах может базироваться на аналогии между распространением электромагнитной волны в дискретной среде и диффузионным движением носителей заряда в твердом теле. В этом случае состояние локализации может характеризоваться отсутствием диффузионного движения волновых процессов. При этом дискретная случайная среда может рассматриваться как сплошная, процесс распространения волн в которой характеризуется эффективным волновым числом keff.
![]() (5)
(5)
где ρ – плотность расположения элементов, f(0) – функция рассеяния в направление вперед одиночного цилиндра [5].
При этом длина свободного пробега волны будет вычисляться по формуле:
l=1/2Im(keff). (6)
Тогда локализационная длина может быть определена как:
lloc = l exp[π/2*Re(keff)*l] (7)
где l вычисляется из формулы (6).
Сравнение результатов и их обсуждение.
В ходе расчетов было установлено, что качественно результаты, полученные строгим и приближенным методами, совпадают (рис 3).
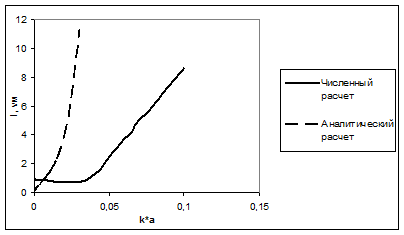
Рис. 3. Зависимость локализационной длины от к*а (при изменение частоты)
Однако, если численное моделирование позволяет определить частотные границы локализации в пределах ka = 0÷0,03, то аналитическое описание процессов приводит к выявлению локализационных состояний в значительно меньшем частотном диапазоне. Таким образом, корректная оценка локализационной длины возможна только на основе строгого описания распространения волн в случайной среде.
Рецензенты:Сандитов Д.С., д.ф.-м.н., профессор, ФГБОУ ВПО Бурятский Государственный Университет, г. Улан-Удэ;
Цыдыпов Ш.Б., д.т.н., доцент, заведующий кафедрой Общей Физики, ФГБОУ ВПО Бурятский Государственный Университет, г. Улан-Удэ.



