Кинетическая модель – это система уравнений, описывающих химические реакции в условиях, где отсутствует сопротивление массо- и теплопереносу, в зависимости от концентраций реагирующих веществ в газовой фазе и на поверхности катализатора, температуры, давления, изменяющихся во всей области параметров, которые встречаются при практической реализации процесса [7]. Кинетическая модель является первым и необходимым этапом при моделировании химических процессов и аппаратов. Поэтому от степени адекватности математического описания кинетической модели зависит выбор оптимальных условий проведения сложной химической реакции [8]. Для прогнозирования поведения химических реакций в любой момент времени в любых условиях используют разработанный ещё в 19 веке закон Гульденберга-Вааге (закон действующих масс). Данный закон утверждает, что скорость изменения концентрация вещества в ходе реакции, пропорциональна произведению концентраций веществ, участвующих в реакции, в соответствующих степенях. Закон действующих масс не всегда позволяет адекватно описывать сложные химические гетерогенные реакции. Особенно те химические системы, когда в реакции одновременно протекают очень медленные и быстрые стадии (когда их скорости сравнимы на 2 и более порядка) [5].
Используя закон действующих масс в качестве базисного, в данной работе мы предложили эволюционному алгоритму уточнить соотношение Гольдберга-Вааге в соответствии с полученными экспериментальными данными. Для уточнения соотношения мы используем метод сетевого оператора, который кодирует композицию функций математического выражения в форме целочисленной матрицы. В качестве эксперимента была взята сложная химическая реакция, в которой участвует 15 веществ, и математическая модель которой содержит 15 дифференциальных уравнений.
Задача идентификации модели химической реакции
Заданы экспериментальные данные по результатам наблюдения прохождения химической реакции
![]() , (1)
, (1)
где ![]() - вектор наблюдаемых параметров химической реакции в момент
- вектор наблюдаемых параметров химической реакции в момент ![]() ,
, ![]() .
.
Известны соотношения, которые описывают зависимость значений параметров реакций от концентраций веществ, участвующих в реакции.
![]() , (2)
, (2)
где ![]() - вектор концентраций веществ в реакции
- вектор концентраций веществ в реакции ![]() .
.
Задана в общем виде математическая модель химической реакции в форме системы обыкновенных дифференциальных уравнений
![]() , (3)
, (3)
где ![]() -вектор взаимодействий веществ,
-вектор взаимодействий веществ, ![]() ,
, ![]() - числовая матрица размерностью
- числовая матрица размерностью ![]() .
.
Компоненты вектора ![]() взаимодействия веществ известны с точностью до веществ, участвующих в взаимодействии. Предполагаем, что во взаимодействии участвуют не более двух веществ
взаимодействия веществ известны с точностью до веществ, участвующих в взаимодействии. Предполагаем, что во взаимодействии участвуют не более двух веществ
![]() ,
,![]()
![]() , (4)
, (4)
где
![]() ,
,![]() , (5)
, (5)
![]() ,
, ![]() , (6)
, (6)
где ![]() - искомые значения компонент вектора параметров
- искомые значения компонент вектора параметров ![]() ,
, ![]() - искомая функция, описывающая взаимодействие веществ
- искомая функция, описывающая взаимодействие веществ ![]() ,
, ![]() .
.
Заданы начальные значения концентраций веществ
![]() . (7)
. (7)
Заданы уравнения химического баланса, которые в терминах задач оптимизации обычно называются ограничениями в виде равенств
![]() ,
, ![]() . (8)
. (8)
Необходимо найти функцию ![]() и значения вектора параметров
и значения вектора параметров ![]() , которые для решения
, которые для решения ![]() уравнений (3) дают минимум функционалам
уравнений (3) дают минимум функционалам
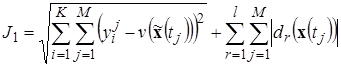 , (9)
, (9)
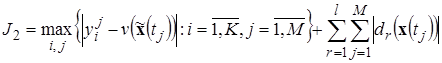 . (10)
. (10)
- Метод сетевого оператора и алгоритм интеллектуальной эволюции
Для решения используем метод сетевого оператора. Данный метод применяет кодировку математического выражения в форме вложенных друг в друга композиций функций. Метод использует только функции с одним или двумя аргументами. Код композиций функций представляется в виде целочисленной верхнетреугольной матрицы, содержащей номера функций. Номера функций с двумя аргументами или бинарных операций указываются на диагонали матрицы. Номера функций с одним аргументом или унарных операций указываются над главной диагональю матрицы. Подробно правила кодирования математических выражений в форме матрицы сетевого оператора изложены в работах [1-3].
Используем многокритериальный вариационный генетический алгоритм или метод интеллектуальной эволюции [4]. Алгоритм осуществляет поиск оптимального математического выражения на множестве малых вариаций некоторых заданных возможных решений, называемых базисными. В алгоритме используем следующие вариации: изменение номера унарной операции, добавление унарной операции, удаление унарной операции и изменение номера бинарной операции. В коде вариации указываем также номер базисного решения, к которому применяются данные вариации.
Множество возможных решений задаем в виде упорядоченного множества базисных матриц сетевого оператора
![]() , (11)
, (11)
где ![]() - матрица сетевого оператора базисного решения
- матрица сетевого оператора базисного решения ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и множества наборов вариаций
, и множества наборов вариаций
![]() , (12)
, (12)
где
![]() , (13)
, (13)
![]() - номер базисной матрицы,
- номер базисной матрицы, ![]() ,
, ![]() - вариация матрицы сетевого оператора,
- вариация матрицы сетевого оператора, ![]() ,
, ![]() - заданная длина вариации.
- заданная длина вариации.
Каждое новое возможное решение получаем после вариации соответствующего базисного решения
![]() , (14)
, (14)
где
![]() .
.
Генетические операции скрещивания и мутации выполняем с упорядоченными множествами наборов вариаций (13).
Одновременно с поиском оптимальной структуры математического выражения в форме матрицы сетевого оператора (14) ищем оптимальное значение вектора параметров ![]() . Каждое возможное решение представляет собой матрицу сетевого оператора
. Каждое возможное решение представляет собой матрицу сетевого оператора ![]() и вектор параметров
и вектор параметров ![]() ,
, ![]() .
.
Для оценки возможных решений ![]() используем ранг Парето, который указывает на количество возможных решений в эволюционирующем множестве, которые лучше в смысле отношения Парето, чем решение
используем ранг Парето, который указывает на количество возможных решений в эволюционирующем множестве, которые лучше в смысле отношения Парето, чем решение ![]() .
.
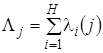 , (15)
, (15)
где
![]() , (16)
, (16)
![]() - значение функционала
- значение функционала ![]() , вычисленное для возможного решения
, вычисленное для возможного решения ![]() ,
, ![]() ,
, ![]() .
.
- Вычислительный эксперимент
В качестве примера рассматриваем химическую реакцию гидроалюминирования олефеинов алюминийорганическими соединениями в присутствие катализатора ![]() [6]. Математическая модель реакции имеет следующий вид
[6]. Математическая модель реакции имеет следующий вид
![]()
![]()
![]()
![]()
![]()
![]()
![]() (17)
(17)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , значения
, значения ![]() зависит от используемого в реакции олефина
зависит от используемого в реакции олефина ![]() ,
, ![]() ,
, ![]() ,
, ![]() - неизвестная функция от трех аргументов,
- неизвестная функция от трех аргументов, ![]() – неизвестные значения постоянных параметров,
– неизвестные значения постоянных параметров, ![]() ,
, ![]() ,
, ![]()
Для данной системы дифференциальных уравнений были заданы следующие начальные условия: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнения баланса имеют вид:
![]()
![]()
![]()
![]() (19)
(19)
![]()
![]()
![]()
![]()
Экспериментальные значения концентрации веществ и моменты времени, в которые она определена, приведены в табл. 1.
При решении данной задачи использовался метод сетевого оператора. Для поиска решения был выбран вариационный генетический алгоритм с множественным базисом. Алгоритм имел следующие значения параметров:
· количество возможных решений в начальной популяции: 256
· число поколений: 2048
· число возможных скрещиваемых пар в поколении: 128
· число вариаций в одном решении: 4
· вероятность мутации: 0,7
· число базисов: 5
· число элитарных решений: 8
· число поколений между сменой базисов: 16
Для реализации поиска на ЭВМ была использована модифицированная программа идентификации математических моделей методом сетевого оператора, осуществляющая промежуточный анализ и сохранение данных популяций. Вычисления проводились на ЭВМ с 4-х ядерным процессором с тактовой частотой 2,8 ГГц. Общее время вычислений составило приблизительно 140 часов.
В результате вычислений был получен сетевой оператор:
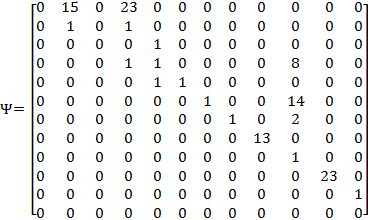 , (20)
, (20)
который соответствует следующему уравнению:
![]() , (21)
, (21)
где ![]() .
.
Графики, построенные на экспериментальных и вычисленных с использованием полученной математической модели значениях, показывающие изменения отношения концентрации веществ ![]() и
и ![]() во времени t, приведены на рис. 1 и рис. 2. Графики изменения отклонений Δ в уравнениях баланса (19) приведены на рис. 3.
во времени t, приведены на рис. 1 и рис. 2. Графики изменения отклонений Δ в уравнениях баланса (19) приведены на рис. 3.
Таблица 1
Экспериментальные данные изменения отношения концентрации веществ ![]() и
и ![]() .
.
|
t, мин |
x3/(x3+x19) |
x19/(x3+x19) |
t, мин |
x3/(x3+x19) |
x19/(x3+x19) |
|
|
5 |
0,9621 |
0,0379 |
175 |
0,3437 |
0,6563 |
|
|
10 |
0,9386 |
0,0614 |
180 |
0,2938 |
0,7062 |
|
|
15 |
0,9034 |
0,0966 |
190 |
0,287 |
0,713 |
|
|
20 |
0,8975 |
0,1025 |
200 |
0,2791 |
0,7209 |
|
|
25 |
0,8994 |
0,1006 |
210 |
0,2713 |
0,7287 |
|
|
30 |
0,8988 |
0,1012 |
220 |
0,2624 |
0,7376 |
|
|
35 |
0,9053 |
0,0947 |
230 |
0,2595 |
0,7405 |
|
|
40 |
0,9112 |
0,0888 |
240 |
0,2498 |
0,7502 |
|
|
45 |
0,9216 |
0,0784 |
250 |
0,2419 |
0,7581 |
|
|
50 |
0,9094 |
0,0906 |
260 |
0,24 |
0,76 |
|
|
55 |
0,9073 |
0,0927 |
270 |
0,2302 |
0,7698 |
|
|
62 |
0,8901 |
0,1099 |
280 |
0,2263 |
0,7737 |
|
|
70 |
0,8897 |
0,1103 |
290 |
0,2184 |
0,7816 |
|
|
75 |
0,8858 |
0,1142 |
300 |
0,2106 |
0,7894 |
|
|
80 |
0,8877 |
0,1123 |
310 |
0,2087 |
0,7913 |
|
|
85 |
0,8857 |
0,1143 |
320 |
0,1969 |
0,8031 |
|
|
90 |
0,8882 |
0,1118 |
330 |
0,191 |
0,809 |
|
|
95 |
0,8779 |
0,1221 |
340 |
0,1852 |
0,8148 |
|
|
100 |
0,8701 |
0,1299 |
350 |
0,1774 |
0,8226 |
|
|
105 |
0,8642 |
0,1358 |
360 |
0,1707 |
0,8293 |
|
|
115 |
0,8466 |
0,1534 |
370 |
0,1656 |
0,8344 |
|
|
125 |
0,832 |
0,168 |
380 |
0,1617 |
0,8383 |
|
|
135 |
0,7371 |
0,2629 |
390 |
0,1558 |
0,8442 |
|
|
145 |
0,6411 |
0,3589 |
400 |
0,15 |
0,85 |
|
|
155 |
0,5517 |
0,4483 |
410 |
0,146 |
0,854 |
|
|
165 |
0,4474 |
0,5526 |
420 |
0,1393 |
0,8607 |
|
|
170 |
0,3965 |
0,6035 |
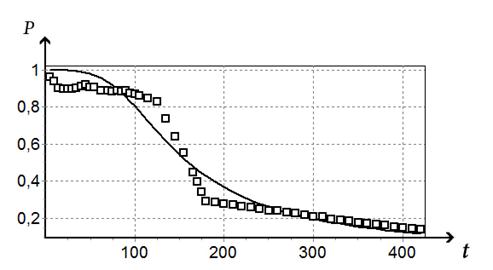
Рис. 1 Экспериментальные (□) и расчетные (—) значения изменения отношения концентрации вещества ![]() (
(![]() )
)
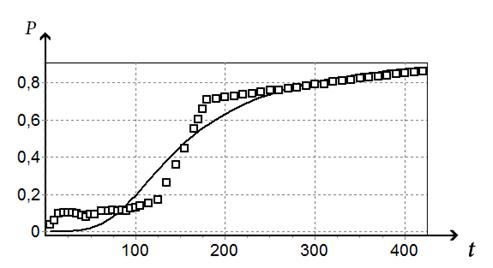
Рис. 2 Экспериментальные (□) и расчетные (—) значения изменения отношения концентрации вещества ![]() (
(![]() )
)
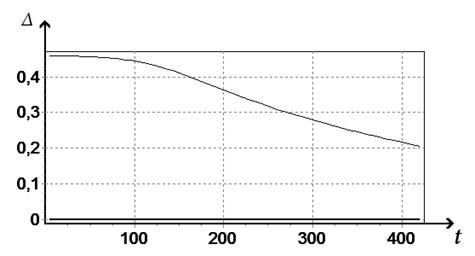
Рис. 3 Графики изменения отклонений Δ в уравнениях баланса (*)
Заключение
Сравнение данных экспериментального и вычислительного экспериментов (рис. 1 и рис. 2) показывает, что предложенный авторами метод вывода кинетических уравнений даёт адекватное описание сложных химических реакций. При этом полученные зависимости изменения концентраций участвующих в реакции веществ от времени сохраняют экспериментально наблюдаемые индукционные периоды. Предсказания условий возникновения и устойчивого существования индукционных периодов позволяют избежать те режимы ведения химических процессов, при которых могут возникнуть нежелательные взрывные процессы, а также прогнозировать реакционную способность исходных реагентов. Например, в рассматриваемых реакциях гидроалюминирования можно количественно описать реакционную способность олефинов.
Данные результаты получены только при одной концентрации катализатора ![]() . В дальнейшим планируется рассмотреть варианты при разных концентрациях катализатора, с разными типами алюминийорганических соединений.
. В дальнейшим планируется рассмотреть варианты при разных концентрациях катализатора, с разными типами алюминийорганических соединений.
Работа выполнена по темам грантов РФФИ №13-08-00523-а и № 12-07-00324-а
Рецензенты:
Карпенко А.П., д.ф.-м.н., профессор, зав. кафедрой ФГБОУ ВПО МГТУ им. Н.Э. Баумана, г.Москва;
Никульчев Е.В., д.т.н., профессор, проректор по научной работе
НОУ ВО Московский технологический институт, г.Москва.



