Пример такого численного решения приведено в работе [2]. При решении этих уравнений в простых физических константах наиболее сложной задачей является нахождение сеточного аналога функции давления, поскольку для этого необходимо решить систему алгебраических уравнений с феноменальным числом уравнений. Решение этой системы не под силу даже современным мощным компьютерам, поэтому данная система может быть решена итерационными методами, которые имеют относительную погрешность, однако менее емкую процедуру решения с точки зрения алгоритмических операций.
Цель исследования – применить итерационные методы решения уравнения для нахождения сеточного аналога функции давления при моделировании трехмерной циркуляции жидкости в озерах.
В работе [2] уравнение Пуассона
приведено к следующему виду, тождественно приравняв правую часть уравнения для
простоты к члену 
,
который в дальнейшем использован как «источниковый» член при нахождении
сеточного аналога функции 
:
, (1)
где 
–
дивергенция скорости; 
–
оператор Лапласа.
Дивергенция скорости в принятых обозначениях имеет формулу:
. (2)
Далее, если заменить дифференциальный
оператор правой части в уравнении (1) конечно-разностной схемой для расчета
члена с
учетом формул, приведенных в работе [2, 6], получим формулу для расчета
«источникового» члена:
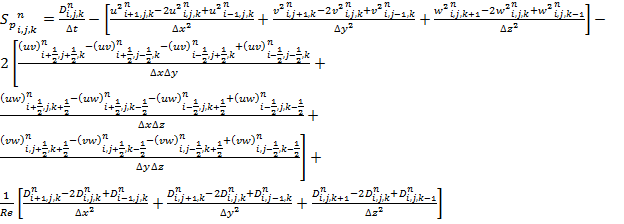, (3)
С учетом использования формул сеточного аналога произведения функций скоростей, которые описаны в работе [2], формула (3) примет вид:
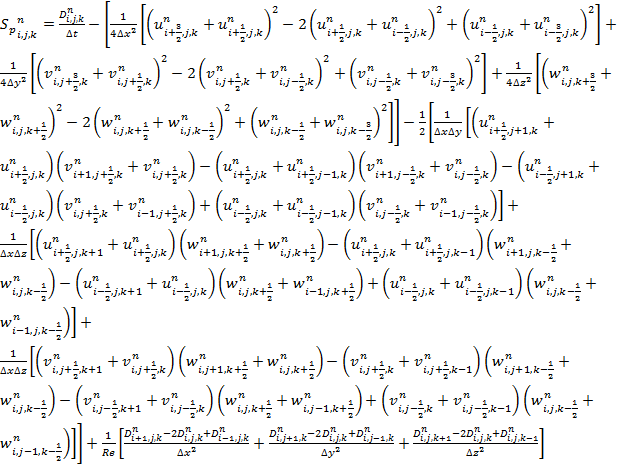. (4)
где конечно-разностный аналог дивергенции скорости имеет вид:
. (5)
После расчета члена 
в
каждой ячейки сеточной области, необходимо произвести расчет сеточного аналога
функции давления 
.
Конечно-разностный аналог левой части уравнения (1) для расчета сеточного
аналога функции давления имеет вид в результате центральной аппроксимации
частных производных второго порядка:
. (6)
Нахождение сеточного аналога функции давления итерационными методами.
Существуют прямые методы решения системы
алгебраических линейных уравнений, образованных уравнением (6), в частности,
метод матричной прогонки. В трехмерной области с размерами узлов по осям 
соответственно
совокупность
данных уравнений и соответствующие граничные условия будут образовывать систему
линейных уравнений, в которой количество уравнений будет иметь значение 
.
Наиболее простыми методами решения такой системы являются правило Крамера и
метод Гаусса. Однако в задачах, представляющих практический интерес, число 
очень
велико, и данные методы становятся не подходящими. Например, при решении
методом Крамера необходимо совершить 
операций.
В этом случае из-за накопления ошибки округления точность решения будет
неудовлетворительной. По этим причинам в наибольший интерес представляют
итерационные методы для решения подобной системы уравнений, поскольку они имеют
значительные преимущества по отношению к прямым методам. На решение системы
уравнений итерационными методами требуется меньше времен; в реализации на ЭВМ
эти методы технологичнее и требуют меньше ресурсов машины; в случае сходимости
данный метод обеспечивает затухание невязки.
Одним из самых простых итерационных
методов для решения системообразующего уравнения относительно сеточного аналога
функции давления является метод Ричардсона. Для этого из уравнения (6) выразим
член .
Данный член будет рассчитываться на итерации 
,
используя значения сеточных функций, полученных на предыдущей операции 
:
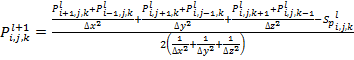. (7)
Таким образом, вычисляется значение
сеточного аналога функции в каждом узле на новой итерации, используя значения
сеточных аналогов функции, полученных на предыдущей итерации.При этом в
расчетах используется значения «источникового» члена 
.
Разность 
в
случае устойчивой схемы стремится к нулю при увеличении в
связи с приближением значения сеточной функции к значению, которое является решением
уравнения (7), то есть колебания ошибки являются затухающими. Поэтому при таком
способе численного решения необходимо ограничиться неким критическим значением
максимального изменения сеточной функции(критерий итерационной сходимости),
взятого из всех узлов сетки между проведенными смежными итерациями, при которой
погрешность решения будет считаться удовлетворительной на данном временном
шаге.
Данное уравнение (7) является двухслойным, поэтому в памяти вычислительной машины необходимо хранить два массива данных при решении данного уравнения. Однако современная вычислительная техника даже персональные ЭВМ имеет колоссальные объемы оперативной памяти по сравнению с возможным количеством данных, содержащихся в данных массивах.
Решение уравнения для нахождения сеточного аналога функции давления методом Либмана
В случае если при обходе точек сетки по
методу Ричардсона вести в направлении возрастания или убывания 
,
,
,
при этом в уравнении (7) использовать уже вычисленные новые значения 
,
то получится схема, которая называется как метод Либмана или метод «итераций
неполными этапами». В случае возрастания ,
,
будем
иметь формулу:
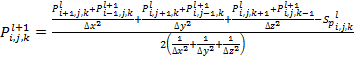. (8)
Необходимо отметить, что для реализации этого алгоритма на ЭВМ, нет необходимости держать в памяти два массива данных. Также к преимуществам этого метода относится более высокая скорость сходимости по сравнению с методом Ричардсона. Однако, поскольку каждое новое вычисляемое значение зависит от только что вычисленного значения, что означает последовательность расчетов, то возможность распараллеливания такого алгоритма не представляется возможным, что является существенным ограничением скорости расчетов для современных ЭВМ.
Решение уравнения для нахождения сеточного аналога функции давления методом последовательной верхней релаксации
Сложим уравнение (8) с тождеством 
,
получим:
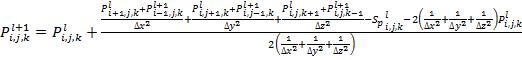. (9)
При приближении к решению, разность стремится
к 0, а значит член, представляющий дробь в уравнении, будет также стремиться к
0. В методе последовательной верхней релаксации данных член умножается на
релаксационный параметр 
,
который не равен 1, в противном случае решение данного уравнения будет
аналогичным, что и описанном в методе Либмана. Уравнение (9) примет вид:
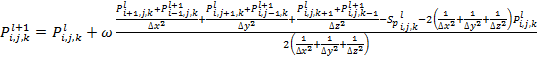. (10)
Для сходимости требуется, чтобы для
параметра выполнялось
неравенство, приведенное в работе [5]:
. (11)
Данный метод имеет большую скорость
сходимости при решении систем уравнений, требующих большого числа итераций, чем
метод Либмана. Однако для достижения оптимальной скорости сходимости необходимо
использование некого оптимально параметра релаксации 
.
Для прямоугольных сеток с простой конфигурацией имеется возможность
аналитического расчета данного параметра. В остальных случаях, данный параметр
находится экспериментально.
Работа выполнена при финансовой поддержке грантов РНФ 14-17-00740 «Озера России - диагноз и прогноз состояния экосистем при климатических и антропогенных воздействиях»
Выводы:
Показаны примеры применения итерационных методов для решения уравнения Пуассона в трехмерном случае моделирования жидкости в простых физических переменных, с помощью которого находится сеточный аналог функции давления в каждом узле сетки, описываемой моделируемое пространство. Данный сеточный аналог функции давления необходим для расчета сеточных аналогов скоростей течений. Приведены способы решения получаемой алгебраической системы методом Ричадсона, методом Либмана (итерации неполными этапами), а также методом последовательной верхней релаксации. Данные методы могут применяться при разработке математических моделей движения жидкости.
Рецензенты:
Филатов Н.Н., д.г.н., член-корреспондент, профессор кафедры Географии Петрозаводского государственного университета, г. Петрозаводск.
Карпечко Ю.В., д.г.н., ведущий научный сотрудник лаборатории географии и гидрологии ИВПС КарНЦ РАН, г. Петрозаводск.