Постановка задачи
Традиционно анализ устойчивости по Ляпунову – предмет качественной теории дифференциальных уравнений. Теоретические методы сложны, трудоемки и, как правило, не допускают компьютерной реализации. В работе предлагается подход к компьютерному анализу устойчивости на основе разностной схемы Эйлера-Коши решений систем обыкновенных дифференциальных уравнений (ОДУ) в нормальной форме, который сводит вопрос об устойчивости к исследованию асимптотического поведения бесконечных произведений, построенных на основе метода Эйлера-Коши. С целью компьютерной реализации анализа устойчивости выполняется циклическое накопление частичных произведений, значения которых при фиксированном шаге разностной схемы пробегают достаточно большой промежуток на полуоси. При данном подходе компьютерный анализ устойчивости сводится к заданию правых частей систем ОДУ и вычислению частичных произведений, попутно получается приближенное решение системы.
Описание общей схемы компьютерного анализа устойчивости
Пусть требуется исследовать устойчивость в смысле Ляпунова решения задачи Коши для нелинейной системы ОДУ в нормальной форме
![]() ,
, ![]() , (1)
, (1)
где ![]() ,
, ![]() – искомое решение,
– искомое решение, ![]() – вектор начальных данных,
– вектор начальных данных, ![]() – заданная вектор-функция от
– заданная вектор-функция от ![]() переменных: независимой переменной
переменных: независимой переменной ![]() и
и ![]() зависимых переменных
зависимых переменных ![]() ,
, ![]() , …,
, …, ![]() .
.
Предполагается, что для системы (1) выполнены все условия существования и единственности решения ![]() на всей полупрямой
на всей полупрямой ![]() . Предполагается, что эти же условия выполнены для всех решений
. Предполагается, что эти же условия выполнены для всех решений ![]() с начальными условиями
с начальными условиями ![]() , если только
, если только
![]() , (2)
, (2)
где ![]() – некоторое постоянное число. Здесь и в дальнейшем под знаком
– некоторое постоянное число. Здесь и в дальнейшем под знаком ![]() понимается каноническая норма вектора.
понимается каноническая норма вектора.
Пусть ![]() – пространство точек
– пространство точек ![]() , или,
, или,![]() . Пусть
. Пусть ![]() множество всех точек
множество всех точек ![]() и
и ![]() в
в ![]() -мерном пространстве
-мерном пространстве ![]() , где
, где ![]() – всевозможные решения, получаемые из (2), при
– всевозможные решения, получаемые из (2), при ![]() .
.
На множестве ![]() предполагаются выполненными условия:
предполагаются выполненными условия:
1) функция ![]() определена и непрерывно дифференцируема по
определена и непрерывно дифференцируема по ![]() на
на ![]() при
при ![]() и всех
и всех ![]() из (2);
из (2);
2) выполнено условие Липшица
![]() ,
, ![]() ; (3)
; (3)
3) существует константа ![]() , такая что
, такая что
![]() . (4)
. (4)
Определение устойчивости по Ляпунову заимствуется из [2] с некоторыми упрощениями, допустимыми в рассматриваемых условиях. Решение ![]() устойчиво (справа), если для любого сколь угодно малого числа
устойчиво (справа), если для любого сколь угодно малого числа ![]() существует
существует ![]() ,
, ![]() , такое что
, такое что ![]() влечет
влечет ![]()
![]() . Решение
. Решение ![]() асимптотически устойчиво (справа), если оно устойчиво и найдется
асимптотически устойчиво (справа), если оно устойчиво и найдется ![]() ,
, ![]() , такое что
, такое что ![]() влечет
влечет ![]() . Всюду ниже рассматривается устойчивость справа (слева аналогично), которая для краткости называется просто устойчивостью.
. Всюду ниже рассматривается устойчивость справа (слева аналогично), которая для краткости называется просто устойчивостью.
Базовая схема излагаемого способа компьютерного анализа устойчивости строится на основе разностных методов приближенного решения ОДУ, ниже для этой цели используется метод Эйлера-Коши. Существенной особенностью при этом является выбор шага численного интегрирования ![]() : предполагается, что для каждого произвольного
: предполагается, что для каждого произвольного ![]() , каково бы ни было
, каково бы ни было ![]() ,
,
![]() ,
, ![]() , (5)
, (5)
изменение переменной ![]() рассматривается как изменение правой границы промежутка
рассматривается как изменение правой границы промежутка ![]() . Иными словами,
. Иными словами, ![]() на любом промежутке
на любом промежутке ![]() , но шаг остается равномерным внутри промежутка.
, но шаг остается равномерным внутри промежутка.
В [4] на основе тейлоровских разложений невозмущенного решения![]() и возмущенного решения
и возмущенного решения ![]() задачи Коши (1) показано, что для разности между соответственными компонентами возмущенного и невозмущенного решений для любого
задачи Коши (1) показано, что для разности между соответственными компонентами возмущенного и невозмущенного решений для любого ![]() из (5) имеет место равенство
из (5) имеет место равенство
![]() ,(6)
,(6)
где величины ![]() суть
суть ![]() и
и
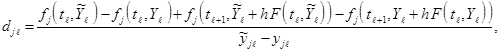
![]() ,(7)
,(7)
где здесь и всюду ниже всегда предполагается, что ![]()
![]() ,
, ![]() .
.
Соотношение (6) является базовым для формулируемых в рамках предложенной схемы условий устойчивости. Первое слагаемое правой части представляет собой главную часть роста возмущения, поскольку не содержит множителя ![]() . В [4] на основании условий (3), (4) доказывается, что
. В [4] на основании условий (3), (4) доказывается, что ![]() при
при![]() , что равносильно
, что равносильно ![]() , для любого
, для любого ![]() из (5). Предельный переход в равенстве (6) влечет
из (5). Предельный переход в равенстве (6) влечет
![]() ,
,![]() , (8)
, (8)
где
![]() . (9)
. (9)
Аналогичные соотношения на основе метода Эйлера приводятся в [5, 6].
Пусть ![]() , где
, где ![]() из (9),
из (9), ![]() из (7),
из (7), ![]() . Непосредственно на основании (8) формулируются условия устойчивости в виде следующей теоремы.
. Непосредственно на основании (8) формулируются условия устойчивости в виде следующей теоремы.
Теорема 1. В условиях 1) – 3) для устойчивости по Ляпунову решения задачи (1) необходимо и достаточно, чтобы существовало ![]() ,
, ![]() , такое, что одновременно для всех решений
, такое, что одновременно для всех решений ![]() при ограничении
при ограничении ![]() выполняется условие
выполняется условие
![]() ,
, ![]()
![]() . (10)
. (10)
Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось (10) и нашлось ![]() ,
, ![]() , такое, что
, такое, что ![]() влечет
влечет
![]() . (11)
. (11)
Условия (10), (11) реализуются программно. Для этого выполняется циклическое накопление частичных произведений 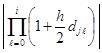 ,
, ![]() , поведение этих произведений будет определять характер устойчивости решения: если при неограниченном росте
, поведение этих произведений будет определять характер устойчивости решения: если при неограниченном росте ![]() будет наблюдаться ограниченность произведений, это будет означать устойчивость, стремление к нулю – асимптотическую устойчивость, неограниченность – неустойчивость. Такое моделирование составляет существо предложенного компьютерного анализа устойчивости.
будет наблюдаться ограниченность произведений, это будет означать устойчивость, стремление к нулю – асимптотическую устойчивость, неограниченность – неустойчивость. Такое моделирование составляет существо предложенного компьютерного анализа устойчивости.
На практике бесконечные произведения не могут быть вычислены точно. Моделирующая их поведение программа с необходимостью остановится на их приближении конечным числом сомножителей. Возникает вопрос, как такое приближение отразится на достоверности оценки устойчивости – необходимо исследовать поведение левых частей соотношений (10), (11) в зависимости от количества сомножителей. Решение этого вопроса дано в [4]. Утверждение теоремы 1 переносится на случай частичных произведений ![]() с некоторыми оговорками, в частности, в формулировку теоремы добавляется, помимо требования существования
с некоторыми оговорками, в частности, в формулировку теоремы добавляется, помимо требования существования ![]() , требование существования номера
, требование существования номера ![]() (шага
(шага ![]() ), начиная с которого выполняется условие
), начиная с которого выполняется условие ![]() ,
, ![]()
![]() . Из предельного перехода в неравенстве
. Из предельного перехода в неравенстве ![]() с учетом (10) следует, что это условие является достаточным для устойчивости решения задачи (1).Как показано в[4],при естественных ограничениях замена предельных значений в выражении условий (10), (11) на их конечные приближения сохраняет достоверность оценки устойчивости.
с учетом (10) следует, что это условие является достаточным для устойчивости решения задачи (1).Как показано в[4],при естественных ограничениях замена предельных значений в выражении условий (10), (11) на их конечные приближения сохраняет достоверность оценки устойчивости.
В [4] показана возможность компьютерного моделирования устойчивости при помощи циклического накопления произведений ![]() , приближаемых как по методу Эйлера-Коши, так и на основе методов Рунге-Кутта и Адамса, аналогичный анализ на основе метода Эйлера выполняется в [5, 6].
, приближаемых как по методу Эйлера-Коши, так и на основе методов Рунге-Кутта и Адамса, аналогичный анализ на основе метода Эйлера выполняется в [5, 6].
Численный эксперимент по моделированию устойчивости
Пусть при ![]() рассматривается система
рассматривается система
![]() ,
, ![]()
![]() ,
, ![]() , (12)
, (12)
общее решение которой ![]() ,
,![]() ,где
,где ![]() ,
,![]() ,
,![]() .
.
В [2] аналитически доказано, что тривиальное решение системы (12) неустойчиво. Ниже этот же результат получается на основе численного моделирования (код программы полностью приводится в [4]). Программные модели представляют собой стандартные подпрограммы Delphi.
В табл.1 результаты численного эксперимента даны при использовании метода Рунге-Кутта 4-го порядка при начальных данных ![]() ,
, ![]() и
и ![]() для шага
для шага ![]() .
.
Таблица 1
Численное моделирование неустойчивости тривиального решения системы (12)
|
|
11.00 |
101.00 |
501.00 |
901.00 |
991.00 |
|
|
1.109E+0001 |
1.010E+0002 |
5.009E+0002 |
9.009E+0002 |
9.909E+0002 |
Норма произведения ![]() на промежутке
на промежутке ![]() возросла от значения 11 до 990, что соответствует неустойчивости тривиального решения.
возросла от значения 11 до 990, что соответствует неустойчивости тривиального решения.
Замечание 1. Из равенства (8) следует, что![]()
![]() Поэтому
Поэтому![]() , где
, где ![]() при
при ![]() ,
, ![]() Иными словами, аналогично норме произведения
Иными словами, аналогично норме произведения ![]() ведет себя отношение разности возмущенного и невозмущенного решений к величине возмущений начальных данных, взятых по норме. Этот факт подтверждается численным экспериментом, результаты которого полностью повторяют данные табл. 1 [4 – 6].
ведет себя отношение разности возмущенного и невозмущенного решений к величине возмущений начальных данных, взятых по норме. Этот факт подтверждается численным экспериментом, результаты которого полностью повторяют данные табл. 1 [4 – 6].
Пусть дана система ОДУ
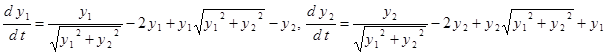 ,(13)
,(13)
где![]() ,
, ![]() . Общее решение системы (13) имеет вид
. Общее решение системы (13) имеет вид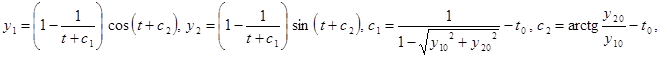
![]() .
.
Решения системы (13) с начальными данными ![]() асимптотически устойчивы, при условии
асимптотически устойчивы, при условии ![]() – устойчивы, если
– устойчивы, если![]() – неустойчивы [3].
– неустойчивы [3].
В табл.2 результаты численного эксперимента даны при использовании метода Эйлера-Коши для начальных данных ![]() ,
, ![]() и
и ![]() с шагом
с шагом![]() .
.
Таблица 2
Численное моделирование асимптотической устойчивости решения системы (13)
|
|
10.00 |
100.00 |
400.00 |
900.00 |
1000.00 |
|
|
1.387E+0000 |
4.320E-0001 |
6.829E-0002 |
2.002E-0002 |
1.371E-0002 |
Норма произведения ![]() на промежутке
на промежутке ![]() убывает к нулю, что согласно (11) интерпретируется как признак асимптотической устойчивости. Стремление нормы к нулю более выражено в случае
убывает к нулю, что согласно (11) интерпретируется как признак асимптотической устойчивости. Стремление нормы к нулю более выражено в случае ![]() (например,
(например, ![]() и
и ![]() ).
).
В табл.3 даны результаты численного эксперимента при использовании метода Рунге-Кутта 4-го порядка для начальных данных ![]() ,
, ![]() и
и ![]() с шагом
с шагом ![]() .
.
Таблица 3
Численное моделирование устойчивости решения системы (13)
|
|
10.00 |
100.00 |
400.00 |
900.00 |
1000.00 |
|
|
1.680E+0000 |
1.749E+0000 |
1.803E+0000 |
2.286E+0000 |
1.926E+0000 |
Норма произведения ![]() на промежутке
на промежутке ![]() изменяется, но в целом не превосходит значения 2.3, что согласно условию (10) является признаком устойчивости.
изменяется, но в целом не превосходит значения 2.3, что согласно условию (10) является признаком устойчивости.
В табл.4 приведены результаты численного эксперимента при использовании метода Адамса 4-го порядка с шагом ![]() для начальных данных
для начальных данных ![]() ,
, ![]() и
и ![]() .
.
Таблица 4
Численное моделирование неустойчивости решения системы (13)
|
|
1.00 |
10.00 |
40.00 |
47.00 |
54.00 |
|
|
1.746E+0000 |
2.514E+0000 |
2.077E+0001 |
1.017E+0002 |
1.393E+0004 |
Норма произведения ![]() на промежутке
на промежутке ![]() монотонно возрастает с большой скоростью, что в продолжение процесса приводит к переполнению, это – нарушение условия (10) и интерпретируется как неустойчивость. Возрастание
монотонно возрастает с большой скоростью, что в продолжение процесса приводит к переполнению, это – нарушение условия (10) и интерпретируется как неустойчивость. Возрастание ![]() более быстро приводит к переполнению при
более быстро приводит к переполнению при![]() .
.
Для численных экспериментов в табл.2 – 4 можно повторить замечание 1.
Изложенный подход к компьютерному анализу устойчивости отличается от известных [1, 2] построением на основе рекуррентных преобразований разностных схем. Отличия сохраняются относительно современного состояния исследований [7 – 9], включая численное моделирование [10], отличие от [5, 6] заключается в использовании разностных методов более высокого порядка.
Заключение
Предложена схема компьютерного анализа устойчивости для систем ОДУ в нормальной форме на основе рекуррентных преобразований разностных приближений решений задачи Коши. Разность между значениями возмущенного и невозмущенного решений выражается как бесконечное произведение, сомножители которого включают в себя разностные приближения и возмущения начальных данных. Асимптотическое поведение таких произведений однозначно определяет характер устойчивости решения. Необходимым и достаточным условием устойчивости является равномерная ограниченность бесконечных произведений на полуоси. Асимптотическая устойчивость имеет место при стремлении этих произведений к нулю с ростом независимой переменной. Развернутый численный и программный эксперимент представлен в [4].
Рецензенты:
Веселов Г.Е., д.т.н., доцент, директор института компьютерных технологий и информационной безопасности ЮФУ, г. Таганрог;
Карелин В.П., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий ТИУиЭ, г. Таганрог.



