1. Цепные дроби являются одним из аппаратов приближения функций. Они обладают замечательным свойством малого накопления погрешности при их вычислении.
Цепной (непрерывной) дробью называется выражение вида
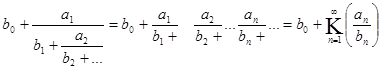(1)
элементы 
цепной дроби (1) могут быть числами (вещественными или комплексными), функциями (одной или многих переменных) [5].
Выражение
называется подходящей дробью (порядка 
) цепной дроби (1). 
называется числителем, 
– знаменателем подходящей дроби 
. Цепная дробь (1) называется сходящейся, если существует конечный
. (2)
Число 
называется значением цепной дроби (1) и пишут
.
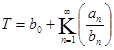Если предел в (2) не существует или существует, но 
, то цепная дробь (1) называется расходящейся (в первом случае существенно, во втором случае несущественно).
Числители и знаменатели подходящих дробей связаны рекуррентными соотношениями
(3)
2. Пусть 
и 
- целые неотрицательные числа и функция 
имеет в промежутке 
непрерывные производные всех порядков до 
включительно. Имеет место формула Обрешкова с остаточным членом
, (4)
где
,
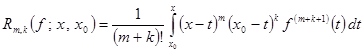которая широко применяется для выяснения общего вида подходящих дробей в теории цепных дробей.
Для 
равенство (4) принимает вид
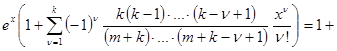
, (5)
где остаточный член в этом случае, после замены переменной 
, принимает вид
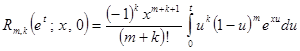. (6)
Так как
,
то равенство (5) можно переписать так
. (7)
Из (6) и (7) следует: если 
– дробь Паде поля 
для функции 
, то
[4].
3. Задача Коши
имеет решение 
.
Разложение функции в степенной ряд имеет вид
, 
– любое.
Разложение в цепную дробь
, для любого .
Здесь, очевидно, имеем 
для 
.
И 
,
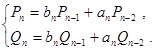для 
.
Через функцию выражаются гиперболические функции
,
,
.
Известно, что
, 
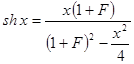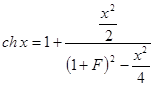, где 
определена формулой
.
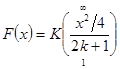Известно ([6], с. 121), что при 
имеет место разложение
.
Дробь сходится на всей плоскости комплексного переменного, за исключением точек несущественной расходимости.
Ниже приводится листинг программы на языке Turbo Pascal для нахождения значений 
, 
и 
с использованием подходящих дробей цепных дробей 10-го порядка для 
и указано приближенное значение этих функций с точностью до 12 знака.
Листинг программы
uses crt;
const n=10;
var b,c:array [1..10] of real;
chcx,shcx,thcx,a,f:real; i:integer;
x:extended;
function sinh(x:extended):extended;
begin
sinh:=(exp(x)-1/exp(x))/2;
end;
function cosh(x:extended):extended;
begin
cosh:=(exp(x)+1/exp(x))/2;
end;
function tanh(x:extended):extended;
begin
tanh:=(exp(2*x)-1)/(exp(2*x)+1);
end;
begin
clrscr;
x:=0.1;
repeat
a:=sqr(x)/4;
b[n]:=2*n+1;
c[n]:=b[n];
for i:=n-1 downto 1 do
begin
b[i]:=2*i+1;
c[i]:=b[i]+a/c[i+1];
end;
f:=a/c[1];
chcx:=(sqr(1+f)+a)/(sqr(1+f)-a);
shcx:=x*(1+f)/(sqr(1+f)-a);
thcx:=x*(1+f)/(sqr(1+f)+a);
writeln(' x | cosh | chcx');
writeln('__________________________________________');
writeln(' ',x:4,'|',cosh(x),'|',chcx);
writeln(' x | sinh | shcx');
writeln('__________________________________________');
writeln(' ',x:4,'|',sinh(x),'|',shcx);
writeln(' x | tanh | thcx');
writeln('__________________________________________');
writeln(' ',x:4,'|',tanh(x),'|',thcx);
writeln;
writeln(' погрешность=',abs(tanh(x)-thcx));
x:=x+0.1;
until x>1.5;
readkey;
end.
Результаты программы (для х=0.1, 0.2, 0.3, 0.4, 0.5)
x | cosh | chcx
__________________________________________________________
1.0E-0001| 1.00500416805580E+0000| 1.00500416805517E+0000
x | sinh | shcx
__________________________________________________________
1.0E-0001| 1.00166750019844E-0001| 1.00166750019866E-0001
x | tanh | thcx
__________________________________________________________
1.0E-0001| 9.96679946249558E-0002| 9.96679946249515E-0002
погрешность = 4.35568736027042E-0015
x | cosh | chcx
__________________________________________________________
2.0E-0001| 1.02006675561908E+0000| 1.02006675561825E+0000
x | sinh | shcx
__________________________________________________________
2.0E-0001| 2.01336002541094E-0001| 2.01336002540984E-0001
x | tanh | thcx
__________________________________________________________
2.0E-0001| 1.97375320224904E-0001| 1.97375320224864E-0001
погрешность = 3.95196706306014E-0014
x | cosh | chcx
__________________________________________________________
3.0E-0001| 1.04533851412886E+0000| 1.04533851412816E+0000
x | sinh | shcx
__________________________________________________________
3.0E-0001| 3.04520293447143E-0001| 3.04520293447240E-0001
x | tanh | thcx
__________________________________________________________
3.0E-0001| 2.91312612451591E-0001| 2.91312612451748E-0001
погрешность = 1.56648728277115E-0013
x | cosh | chcx
__________________________________________________________
4.0E-0001| 1.08107237183845E+0000| 1.08107237183867E+0000
x | sinh | shcx
__________________________________________________________
4.0E-0001| 4.10752325802816E-0001| 4.10752325802605E-0001
x | tanh | thcx
__________________________________________________________
4.0E-0001| 3.79948962255225E-0001| 3.79948962255185E-0001
погрешность = 4.02884377335294E-0014
x | cosh | chcx
__________________________________________________________
5.0E-0001| 1.12762596520638E+0000| 1.12762596520588E+0000
x | sinh | shcx
__________________________________________________________
5.0E-0001| 5.21095305493747E-0001| 5.21095305493873E-0001
x | tanh | thcx
__________________________________________________________
5.0E-0001| 4.62117157260010E-0001| 4.62117157259854E-0001
погрешность = 1.55619684890154E-0013
Из полученных значений для погрешностей видно, что данный способ интерполирования является более точным.
Рецензенты:
Рамазанов А.-Р.К., д.ф.-м.н., профессор, заведующий кафедрой математического анализа ФГБОУ ВПО «Дагестанский государственный университет», г. Махачкала;
Баламирзоев А.Г., д.т.н., профессор, ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала.