В настоящее время разработчики высоковольтных сильноточных электрических аппаратов и других устройств силовой электроэнергетики стремятся там, где это возможно, заменять медь как основной материал элементов токоведущих систем на другие, более дешевые материалы, в частности на алюминий и его сплавы. Это вызвано интенсивным опережающим ростом цен на медь на мировых рынках: за последние 10 лет цена на медь выросла примерно в 5 раз. Основным препятствием на пути такой замены является меньшая электропроводность алюминия по сравнению с медью, что приводит к дополнительным тепловым потерям и ухудшению теплового режима аппаратов при протекании номинальных токов.
Возникают и другие проблемы. Например, значительное снижение стойкости контактных соединений к ударным токам короткого замыкания из-за довольно низкой температуры плавления алюминия. Эту трудность можно отчасти обойти, применяя контакт-детали со слоистой структурой. Основным материалом является алюминий, на поверхность которого тем или иным способом наносится небольшой по толщине слой меди. Основными способами создания медного покрытия являются напыление и плакирование [2]. При этом получается разное по качеству сцепление нанесенного слоя с подложкой и, следовательно, покрытия разного качества. В зависимости от технологии нанесения меди и условий эксплуатации контакта ее толщина может варьироваться в широких пределах – от десятков микрон до единиц миллиметров. Влияние свойств покрытия, в частности степени шероховатости его поверхности, а также качества сцепления слоя меди с алюминиевой подложкой на стойкость контактов к протекающему через них току будет рассматриваться нами в следующих работах с привлечением методов экспериментального исследования. Здесь же мы проведем оценку влияния толщины покрытия на динамику нагрева контактов путем проведения численных расчетов.
Исследуемая модель и результаты численных расчетов. В работе проводится численное моделирование процесса импульсного нагрева слоистых контактов, в качестве которых используются два цилиндрических электрода, соединенные одним контактным пятном круглой формы, расположенным на оси симметрии. Радиус контактного пятна выбран равным 0,5 мм. Такой размер характерен для сильноточных контактов. При этом само пятно считается полностью проводящим. Влияние фрагментации на параметры сильноточных электрических контактов было оценено нами в [4]. Исследуемые контакты схематично изображены на рис. 1, где показано их сечение, проходящее через ось симметрии, линии тока и равного потенциала. Численное решение задачи строится в программном комплексе ANSYS.
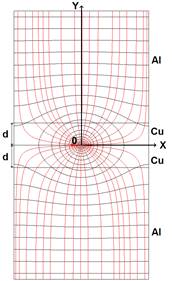
Рис. 1. Цилиндрические контакты со слоистой структурой.
Процесс прохождения тока через контакты без учета термоэлектрических эффектов описывается следующей системой уравнений:
![]() (1)
(1)
![]() (2)
(2)
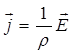 (3)
(3)
![]() (4)
(4)
где T – температура, j – плотность электрического тока, φ – электрический потенциал, E – напряженность электрического поля, ρ – удельное сопротивление материала, κ – теплопроводность, γ – плотность, сp – теплоемкость. Уравнения (1) – (3) связывают электрический потенциал, напряженность электрического поля и плотность тока, уравнение (4) – это нестационарное уравнение теплопроводности с объемным источником тепловыделения. К настоящему времени нет единого мнения о том, нужно ли учитывать термоэлектрические токи при нагреве сильноточных электрических контактов [1; 5]. Однако для случая, когда контактирующие поверхности выполнены из меди, их наличием можно пренебречь на фоне токов проводимости [3].
В качестве токового воздействия зададим импульс прямоугольной формы длительностью 10 мс. Амплитуду будем выбирать таким образом, чтобы максимальная температура достигала температуры плавления. Выбор длительности продиктован тем, что при прохождении тока короткого замыкания плавление происходит в течение первого полупериода (с учетом апериодической составляющей тока). Получающиеся данные о нагреве при таком токовом воздействии позволят сделать некоторые выводы о стойкости контактов со слоистой структурой к ударному току. В силу малой длительности нагрева на всех внешних поверхностях задавалось граничное условие, соответствующее отсутствию теплообмена с окружающей средой. На границах раздела Cu-Al задавались непрерывными потенциал и температура, а также значения плотности электрического тока и теплового потока.
Приведем распределение температуры в окрестности контактного пятна в предельном случае бесконечно толстого слоя меди ![]() (случай чисто медных контактов), рис. 2. Максимум температуры расположен на краю пятна. Фронт тепла за время действия импульса тока распространяется на расстояние
(случай чисто медных контактов), рис. 2. Максимум температуры расположен на краю пятна. Фронт тепла за время действия импульса тока распространяется на расстояние ![]() порядка нескольких радиусов контактного пятна.
порядка нескольких радиусов контактного пятна.
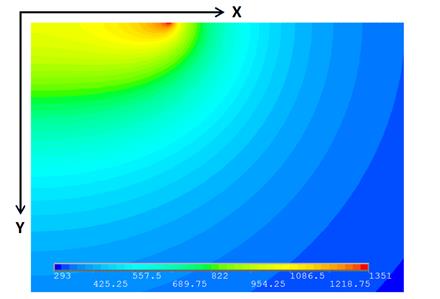
Рис. 2. Распределение температуры в окрестности контактного пятна при ![]() .
.
В случае слоистых электродов при толщине медного слоя меньше ![]() произойдет искажение теплового поля в силу различия свойств материала меди и алюминия (табл. 1).
произойдет искажение теплового поля в силу различия свойств материала меди и алюминия (табл. 1).
Таблица 1
Свойства Cu и Al при НКУ
|
|
Cu |
Al |
|
γ, кг/м3 |
8890 |
2700 |
|
κ, Вт/(м*К) |
385 |
236 |
|
сp, Дж/(кг*К) |
349 |
900 |
|
Tпл, K |
1356 |
933 |
Проследим за температурой на границе раздела меди и алюминия, уменьшая толщину медного слоя начиная со значения ![]() , и подбирая ток
, и подбирая ток ![]() для каждой толщины таким, чтобы достигалась температура плавления меди. При этом можно определить то пороговое значение толщины медного покрытия
для каждой толщины таким, чтобы достигалась температура плавления меди. При этом можно определить то пороговое значение толщины медного покрытия ![]() , которое разделяет два разных типа плавления. При
, которое разделяет два разных типа плавления. При ![]() плавление начинается в области контактного пятна (плавится медь), в обратном случае – на границе раздела (плавится алюминий). На рис. 3 приведены распределения температуры вдоль оси
плавление начинается в области контактного пятна (плавится медь), в обратном случае – на границе раздела (плавится алюминий). На рис. 3 приведены распределения температуры вдоль оси ![]() , проходящей по границе раздела Cu-Al при разной толщине медного слоя. Штрихпунктирной линией обозначена величина температуры плавления алюминия. Из данной серии графиков можно определить значение предельной толщины слоя меди. Для длительности нагрева
, проходящей по границе раздела Cu-Al при разной толщине медного слоя. Штрихпунктирной линией обозначена величина температуры плавления алюминия. Из данной серии графиков можно определить значение предельной толщины слоя меди. Для длительности нагрева ![]() оно составляет
оно составляет![]() .
.
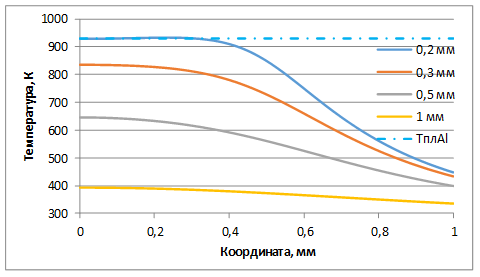
Рис. 3. Распределение температуры на границе раздела Cu-Al при ![]() .
.
Определим понятие предельно допустимого импульсного тока для слоистых контактов.
Это такое значение тока, при котором к моменту окончания его действия достигается либо температура плавления меди в области контактного пятна (соответствующее значение тока обозначено ![]() ), либо температура плавления алюминия на границе раздела двух металлов (ток обозначен
), либо температура плавления алюминия на границе раздела двух металлов (ток обозначен ![]() ):
):
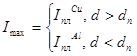
Тогда при выполнении условия ![]() плавления контактов не произойдет.
плавления контактов не произойдет.
Зависимость ![]() от толщины медного слоя и уровень тока
от толщины медного слоя и уровень тока ![]() , который приводит к плавлению в случае чисто медных электродов, представлены на рис. 4. Область, расположенная под кривой, соответствует таким значениям импульсного тока и толщины покрытия, при которых не происходит плавления контактов ни в области контактного пятна, ни на границе раздела металлов. Можно предположить, что при выходе за пределы этой области работоспособность контактов будет нарушена. Такое предположение основано на результатах экспериментальных исследований по прохождению ударных токов через сильноточные контакты [6].
, который приводит к плавлению в случае чисто медных электродов, представлены на рис. 4. Область, расположенная под кривой, соответствует таким значениям импульсного тока и толщины покрытия, при которых не происходит плавления контактов ни в области контактного пятна, ни на границе раздела металлов. Можно предположить, что при выходе за пределы этой области работоспособность контактов будет нарушена. Такое предположение основано на результатах экспериментальных исследований по прохождению ударных токов через сильноточные контакты [6].
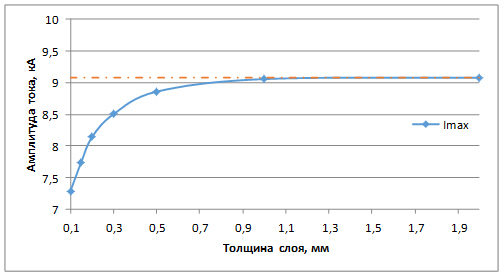
Рис. 4. Зависимость предельно допустимого тока от толщины покрытия.
Толщина медного покрытия существенно влияет на динамику нагрева контактной области, что подтверждается семейством кривых, описывающих изменение во времени максимальной температуры контактов для различных значений параметра d (рис. 5).
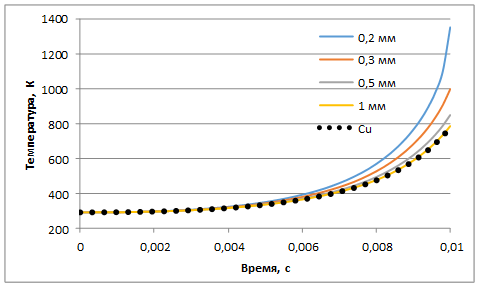
Рис. 5. Зависимость максимальной температуры контактов от времени при различных значениях толщины покрытия.
Заключение
Проведено исследование импульсного нагрева протекающим током алюминиевых контактов с медным покрытием в широком диапазоне температур, вплоть до начала плавления. Показано, что в зависимости от толщины медного слоя плавление может начинаться либо в области контактного пятна, либо на границе раздела двух металлов. Введено понятие предельно допустимого тока, при котором плавление контактов еще не происходит, получена его зависимость от толщины покрытия. Построены кривые нагрева слоистых контактов, определяющие изменение во времени максимальной температуры в окрестности контактного пятна. При толщине покрытия, равной диаметру контактного пятна, величина предельного тока практически не отличается от соответствующей величины для чисто медных контактов при рассмотренных токовых воздействиях. Приведенные в работе зависимости позволяют оценить уменьшение величины предельно допустимого тока и роста максимальной температуры контактов при использовании покрытий меньшей толщины.
Рецензенты:
Ключарев А.Н., д.ф.-м.н, профессор, кафедра оптики, физический факультет, Санкт-Петербургский государственный университет, г. Санкт-Петербург.
Бисярин М.А.. д.ф.-м.н, профессор, Санкт-Петербургский государственный университет, физический факультет, кафедра радиофизики, г. Санкт-Петербург.



