С целью интенсификации нефтеизвлечения из продуктивных пластов применяются различные физические, химические и гидродинамические методы. В последние годы отечественные и зарубежные исследователи уделяют значительное внимание акустическим методам повышения нефтеотдачи как наиболее перспективным по своим техническим возможностям, экономичным и экологически чистым. Развитие теории акустического воздействия на пористую среду позволит более эффективно использовать этот метод на практике [1-3, 5, 9, 10, 13, 14].
В данной работе считается, что основным механизмом, переводящим энергию волнового поля в пористой среде в тепло, является сила вязкого трения между насыщающей жидкостью и скелетом в пористой среде. Построена функция объемного источника тепла для процесса нагрева пористой среды с помощью акустического поля. Выполнен анализ зависимости фазовой скорости и коэффициента затухания волны от круговой частоты. Исследовано температурное поле в пористой среде при разных значениях частоты акустического поля.
1. Основные уравнения. Рассматривается пористая среда, насыщенная жидкостью, на границе 
которой действует источник гармонических волн давления. Под действием источника волн давления жидкость будет совершать колебательные движения относительно скелета пористой среды. Чтобы описать исследуемый процесс примем следующие допущения: пористый скелет несжимаемый; температуры жидкости и скелета пористой среды в каждой точке совпадают.
С учетом принятых допущений запишем уравнения, описывающие исследуемый процесс. Закон сохранения массы жидкости при отсутствии источников массы запишем в форме [8, 16]
. (1)
Здесь 
– пористость; 
– возмущение плотности жидкости; 
– плотность жидкости, соответствующая невозмущенному состоянию; 
– скорость фильтрации жидкости.
В случае нестационарной фильтрации жидкости в уравнении движения необходимо учесть действие объемной силы трения [15]
, 
, (2)
где 
– возмущение давления в жидкости; 
– коэффициент проницаемости пористой среды; 
– динамическая вязкость жидкости.
Уравнение состояния жидкости в пористой среде примем в виде [4, 6, 7, 11, 12]
. (3)
Наличие источника гармонических волн давления на границе 
может быть записано в виде следующего граничного условия:
, 
, (4)
где 
и 
– амплитуда и круговая частота волны.
Для правой границы рассмотрим случай, когда пористая среда имеет конечную ширину (
) и граница при 
высокопроницаемая, т.е. призабойная зона шириной равной 
засорена (область ), а за этой зоной (
) начинается не засоренная область с проницаемостью во много раз превышающей ее значение в призабойной зоне. Граничное условие записывается в виде
, 
. (5)
Из системы (1)-(3) после некоторых преобразований получаем уравнение, где неизвестной величиной является только давление. Решение полученного уравнения ищем в виде
. (6)
Здесь 
– комплексное волновое число, 
и 
– неизвестные константы; 
– мнимая единица. В выражении (6) первый член описывает распространение волны от источника по направлению координаты х, а второй – в обратном направлении. С учетом граничных условий (4) и (5) получим
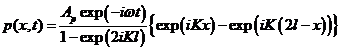, . (7)
Комплексное волновое число 
определяется по формуле
, 
, 
, 
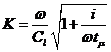. (8)
На рис. 2 приведены зависимости фазовой скорости 
и коэффициента затухания d от круговой частоты w для следующих значений параметров системы 
, 
, 
. Линиям 1 соответствуют значения параметров 
; 2 – 
; 3 – 
; 4 – 
. Видно, что при малых частотах волна распространяется с малой скоростью и большим затуханием. С увеличением значения коэффициента проницаемости фазовая скорость увеличивается, а с увеличением коэффициента пористости фазовая скорость уменьшается. При увеличении значения коэффициента проницаемости на порядок величина коэффициента затухания уменьшается примерно в пять раз, а при увеличении значения коэффициента пористости в два раза величина коэффициента затухания увеличивается примерно в два раза.
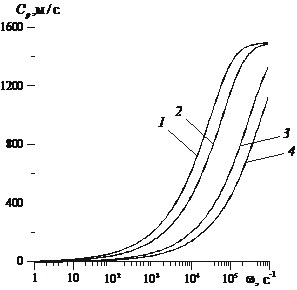
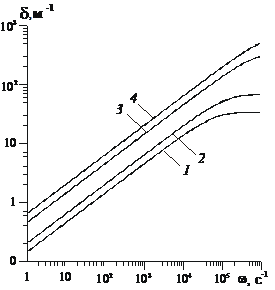
Рис. 1. Зависимости фазовой скорости и коэффициента затухания от круговой частоты.
Аналогично формуле (7) для вычисления скорости фильтрации жидкости получаем следующее выражение
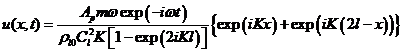. (9)
Под воздействием гармонических волн давления насыщающая пористую среду жидкость совершает колебательное движение относительно твердого скелета. За счет сил трения между жидкостью и скелетом энергия волны переходит в тепло. Объемная сила трения при относительном движении фаз (жидкости относительно скелета) равна [16]
. (10)
Здесь 
означает действительную часть от комплексной величины 
.
Мощность диссипируемой энергии акустического поля в единице объема пористой среды равна мощности объемной силы трения
, (11)
где 
– истинная скорость движения жидкости 
.
Поскольку в реальных процессах, представляющих практический интерес, характерное время воздействия полем значительно больше, чем период колебаний акустических волн 
, то наиболее важным параметром является средний приток тепла в единицу объема за единицу времени
. (12)
2. Температурная задача. Уравнение притока тепла в пористую среду, насыщенную жидкостью, с учетом объемного источника тепла, связанного с вязкостным затуханием акустического поля, запишем в виде
, (13)
, 
, 
.
Здесь 
, 
и 
– плотность, теплоемкость и теплопроводность материала скелета пористой среды; 
и 
– теплоемкость и теплопроводность жидкости.
Начальное условие для температуры примем в виде
, 
. (14)
Будем полагать, что граница 
теплоизолирована
, . (15)
На границе 
происходит теплообмен с окружающей средой. Температура и поток тепла на границе 
непрерывны:
, 
, 
. (16)
Здесь 
означает скачок параметра 
.
На основе уравнения теплопроводности (13) с начальным и граничными условиями (14) – (16) проведены расчеты с целью анализа особенностей нагрева пористой среды, насыщенной водой, в зависимости от параметров пористой среды и характеристик акустического поля. Уравнение (13) решалось численно с помощью метода прогонки. На рис. 2 представлено температурное поле в пористой среде после двухчасового воздействия на нее акустическим полем. Линии 1 соответствуют параметры – 
, 
; линии 2 – 
, 
; линии 3 – 
, 
. Мощность акустического поля во всех трех случаях одинакова и равна 
. Параметры пористой среды: 
, 
. Видно, что увеличение круговой частоты акустического поля приводит только к локализации тепла в приграничной зоне.
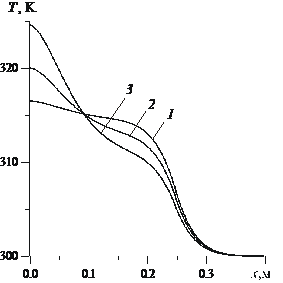
Рис. 2. Температурное поле в пористой среде при разных значениях частоты акустического поля.
На рис. 3. демонстрируется нагрев низкопроницаемой пористой среды воздействием акустического поля. Линии 1 соответствуют параметры – 
, 
; линии 2 – 
, 
.
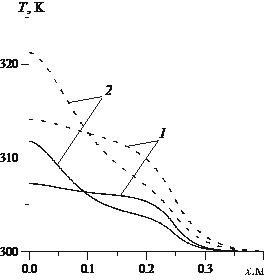
Рис. 3. Температурное поле в низкопроницаемой пористой среде.
Сплошные линии соответствуют двухчасовому воздействию акустическим полем на пористую среду, а штриховые – четырехчасовому воздействию. Мощность акустического поля во всех случаях одинакова и равна 
. Параметры пористой среды: 
, 
. Видно, что для более глубокого и равномерного прогревания низкопроницаемой пористой среды необходимо варьировать частотой.
Выводы. Разработанная математическая модель нагрева пористых сред с помощью акустического поля может быть использована для определения оптимальных параметров поля на практике, при которых получится наиболее эффективный нагрев пористой среды.
Работа выполнена при поддержке гранта СФ БашГУ № В14-19.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор кафедры математического моделирования, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», г.Стерлитамак.
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.