Бицентрическое монофокусное полупространство (БМП) – субъективная модель представления традиционного трёхмерного пространства человеческим сознанием. Суть параллельного переноса в БМП [2] заключается в том, что некоторый объект переносится вдоль радиус-вектора фокуса на расстояние, равное расстоянию между точками исходного и смещённого фокуса в направлении начала координат. При этом считается, что первоначально человек видел предмет, сфокусировав глаза в точке исходного фокуса, а в конце – в точке смещённого фокуса. Хотя предмет, как и фокус, должен переместиться, наблюдателю должно казаться, что исходный и перемещённый объекты одинаковы или что предмет вообще не был перемещён. То есть объект в результате перемещения должен на самом деле исказиться, чтобы казаться человеку эквивалентным своему состоянию в начальном положении.
Хотя человек, обладая бинокулярным зрением, видит каждую точку пространства под двумя ракурсами, его сознание объединяет два полученных изображения в единый корковый образ [5]. При параллельном переносе в БМП смещённый объект должен полностью загораживать исходный, поэтому было выдвинуто предположение о том, что необходимо закрывать каждую область исходной [4].
Получается, что каждая точка пространства находится в ареале, контролируемом в большей степени одним из зрительных центров или обоими приблизительно в равной степени. Важно отметить, что при этом центры устремлены в точку исходного или смещённого фокуса, принадлежащую радиус-вектору исходного фокуса (поскольку радиус-вектор смещённого фокуса принадлежит ему, сонаправлен с ним и не превышает его длины). Тогда выделяются три области точек пространства, над которыми в процессе их обозрения доминируют зрительные центры. Это области зрительных приоритетов или LOR-области [3].
Зрительный приоритет правого центра распространяется на ареал БМП под контролем правого зрительного центра. Зрительный приоритет левого центра соответствует доминированию левого зрительного центра в заданной области пространства. Зрительный приоритет начала координат, или зрительный приоритет среднего центра, – это равноправный обзор определённой части пространства обоими зрительными центрами.
Исходная точка и соответствующая ей смещённая точка относятся к области зрительного приоритета одного и того же центра [3].
Цель исследования
Предстоит выяснить, каким образом следует выделять области зрительных приоритетов, распределяя между ними всё доступное полупространство.
Материалы и методы
Исследование представляет собой логические рассуждения с выводами и математические расчёты на основе данных и принципов, описанных в положениях БМП-подхода [1].
Положение 22 БМП-подхода [1] гласит, что точки исходного и смещённого фокуса лежат на одной прямой, содержащей радиус-вектор исходного фокуса, а положение 27 БМП-подхода [1] заключает, что исходная точка и соответствующая ей смещённая точка относятся к области зрительного приоритета одного и того же центра. Эти утверждения позволяют сделать следующий вывод: распределение LOR-областей зависит не столько от координат x0, y0 ≥ 0 и z0 точки фокуса F по осям OX, OY и OZ соответственно, сколько от направления радиус-вектора OF = f фокуса F, выражающегося величинами его углов α, β и γ наклона к соответствующим координатным осям OX, OY и OZ (см. положение 18 БМП-подхода [1]). Знание координат x0, y0 ≥ 0 и z0 в этом случае необходимо только для построения радиус-вектора f для дальнейшего определения углов α, β и γ. Поскольку существенным оказывается лишь само направление радиус-вектора f фокуса F (а именно, углы α, β и γ), распределение областей зрительных приоритетов будет одинаковым для всех точек фокуса F, принадлежащих одной прямой OF, проходящей через начало координат O.
Было рассмотрено 5 случаев распределения LOR-областей, связанных с направлением радиус-вектора f фокуса F.
Случай 1. Человек смотрит прямо перед собой, и его взгляд сосредоточен на некоторой точке на уровне горизонта, равноудалённой от обоих глаз. В терминах БМП-подхода это означает, что точка фокуса F принадлежит горизонтальной оси OY (F ϵ OY => OF ϵ OY => f ϵ OY): x0 = 0, z0 = 0, y0 ≥ 0, а F(0; y0; 0) - координаты точки фокуса.
Случай 2. Особняком стоит случай расположения точки фокуса в начале координат, когда F = O(0; 0; 0) - тогда человек сводит глаза к носу, причём настолько, что они видят только переносицу с разных сторон в попытке смотреть друг на друга. В реальности этот идеальный случай не достижим, и точка фокуса F всё равно имеет небольшое ненулевое значение ординаты y0 > 0. Хотя, если предположить существование такого момента, субъект не будет способен различать ничего внятно, следовательно, наблюдение исходной и смещённой поверхности вообще будет лишено смысла. Для выделения исключительности данного случая можно условно отнести все точки БМП к одной LOR-области, и пусть это будет ареал влияния среднего центра O.
Все три зрительных центра - L, O, R - принадлежат одной оси OX. Сложно сказать, что будет видеть человек, если точка фокуса находится на этой оси: F ϵ OX. Очевидно, что в случае расположения F на отрезке между глаз имеет место та же ситуация, что и при F = O. Если в идеале человек смотрит обоими глазами вправо, наблюдая точку на положительной полуоси OX, или же влево, глядя на точку фокуса F на отрицательной части OX, субъект должен видеть только правые или левые границы своих глазниц. Тогда точки полупространства сложно будет отнести к области влияния только одного левого центра L, если человек смотрит вправо, или к ареалу правого центра R, когда наблюдатель смотрит влево, хотя это на первый взгляд логично. Оба глаза находятся в одинаковом положении, причём ничего существенного различить не могут - случай спорный, и всё полупространство следует условно закрепить за средним центром O.
Случай 3. Человек концентрирует свой взгляд на линии горизонта и наблюдает на ней точку, находящуюся на разном расстоянии от своих глаз. В терминах БМП-подхода это означает, что точка фокуса F принадлежит горизонтальной плоскости XOY (F ϵ XOY => OF ϵ XOY => f ϵ XOY). Следует отметить, что ось абсцисс также лежит в горизонтальной плоскости (OX ϵ XOY), но вариант расположения точки фокуса F на ней (F ϵ OX) уже был рассмотрен ранее - это случай № 2. Ось ординат тоже находится в координатной плоскости XOY: OY ϵ XOY, и, когда точка фокуса F ей принадлежит (F ϵ OY), возникает случай № 1. Значит, на текущий момент следует исключить уже рассмотренные варианты.
Случай 4. Ещё один исключительный случай, когда теоретически человек остановил свой взгляд во фронтальной плоскости XOZ. Конечно, где бы ни находилась точка в этой плоскости, кроме контуров собственных глазниц, субъект не будет способен что-либо различить. Однако данная ситуация всё же представляет интерес для распределения зрительных приоритетов, поскольку ранее рассматривались случаи расположения точки фокуса в вертикальной и горизонтальной плоскостях YOZ и XOY соответственно. В терминах БМП-подхода это выражается как то, что точка фокуса F принадлежит фронтальной плоскости XOZ (F ϵ XOZ => OF ϵ XOZ => f ϵ XOZ). Следует отметить, что ось абсцисс также лежит во фронтальной плоскости (OX ϵ XOZ), но вариант расположения точки фокуса F на ней (F ϵ OX) уже был рассмотрен ранее - это случай № 2. Ось аппликат тоже находится в координатной плоскости XOZ: OZ ϵ XOZ, и, когда точка фокуса F ей принадлежит (F ϵ OZ), возникает случай № 1. Значит, на текущий момент следует исключить уже рассмотренные варианты.
Случай 5. Случай общего вида, когда человек наблюдает произвольную точку пространства, не принадлежащую координатным плоскостям, поскольку все эти случаи были ранее рассмотрены.
Результаты и их обсуждение
По итогам проведённых исследований была сформулирована гипотеза о распределении областей зрительных приоритетов, положения которой приведены ниже.
Положение 1. Распределение областей зрительных приоритетов будет одинаковым для всех положений точки фокуса F (x0; y0; z0), в пределах одной прямой OF, проходящей через начало координат O (0; 0; 0) (O ϵ OF) и, следовательно, содержащей радиус-вектор фокуса: f = OF ϵ OF.
Положение 2. Каждой точке T(x; y; z) в БМП сопоставляется некоторый зрительный центр A (k; 0; 0), где k - абсцисса точки A, равная d, ‒d или 0 (2d - межцентровое расстояние, а d - его половина). A соответствует среднему центру O (0; 0; 0), правому центру R (d; 0; 0) или левому центру L (‒d; 0; 0). Этот зрительный центр A получает приоритет во влиянии на точку T.
Положение 3. Через вертикальную ось OZ перпендикулярно координатной плоскости XOY проходит вертикальная плоскость вращения ς (уравнение: x ‒ y ∙ x0 / y0 = 0), содержащая радиус-вектор f фокуса F (x0; y0; z0):O(0; 0; 0) ϵ f ϵ ς, ς перпендикулярно XOY, OZ ϵ ς - см. рис. 1. При нулевой абсциссе x0 = 0 точки фокуса F плоскость ς не различима, потому что совпадает с координатной плоскостью YOZ (ς = YOZ). Если абсцисса x0 ≠ 0 и ордината y0 ≠ 0 точки фокуса F не равны нулю, то проявляется вращение плоскости ς вокруг оси OZ.
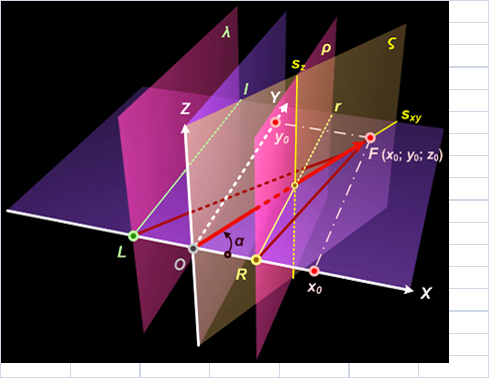
Рисунок 1.Точка фокуса F в плоскости XOY
Точка T (x; y; z), принадлежащая ς (T ϵ ς), относится к среднему центру O (0; 0; 0). Если точка T локализуется правее плоскости ς, то она находятся под контролем правого зрительного центра R (d; 0; 0). А левый центр L (‒d; 0; 0) имеет приоритет во влиянии на точку T, когда она расположена левее плоскости ς.
Случай № 3 концентрирует внимание на плоскости ς, когда x0 ≠ 0, y0 ≠ 0, а z0 = 0 - см. рис. 1.
Положение 4. Через горизонтальную ось OY перпендикулярно координатной плоскости XOZ проходит горизонтальная плоскость вращения γ (уравнение: x ‒ z ∙ x0 / z0 = 0), содержащая радиус-вектор f фокуса F (x0; y0; z0): O (0; 0; 0) ϵ f ϵ γ,γ перпендикулярно XOZ, OY ϵ γ - см. рис. 2. При нулевой абсциссе x0 = 0 точки фокуса F плоскость γ не различима, потому что совпадает с координатной плоскостью YOZ (γ = YOZ). Если абсцисса x0 ≠ 0 и аппликата z0 ≠ 0 точки фокуса F не равны нулю, то проявляется вращение плоскости γ вокруг оси OY.
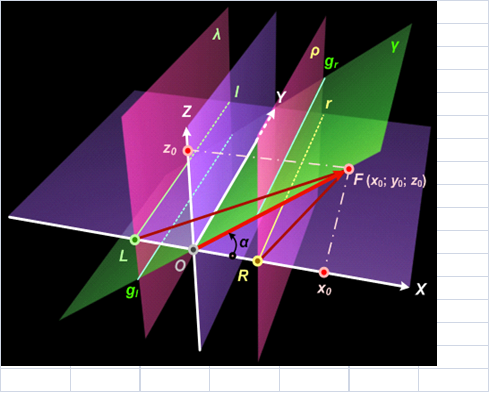
Рисунок 2.Точка фокуса F в плоскости XOZ
Точка T (x; y; z), принадлежащая γ (T ϵ γ), относится к среднему центру O (0; 0; 0). Если точка T локализуется правее плоскости γ, то она находится под контролем правого зрительного центра R (d; 0; 0). А левый центр L (‒d; 0; 0) имеет приоритет во влиянии на точку T, когда она расположена левее плоскости γ.
Случай № 4 концентрирует внимание на плоскости γ, когда x0 ≠ 0, z0 ≠ 0, а y0 = 0 - см. рис. 2.
Положение 5. Когда точка фокуса F (x0; y0; z0) имеет нулевую абсциссу x0 = 0, то есть принадлежит координатной плоскости YOZ (F ϵ YOZ), плоскости ς и γ не видны, так как совпадают с YOZ (ς = γ = YOZ, уравнение этих плоскостей: x = 0).
Точка T(x; y; z), принадлежащая вертикальной координатной плоскости YOZ (T ϵ YOZ = ς = γ), относится к среднему центру O (0; 0; 0). Если точка T локализуется правее плоскости YOZ, то она находится под контролем правого зрительного центра R (d; 0; 0). А левый центр L (‒d; 0; 0) имеет приоритет во влиянии на точку T, когда она расположена левее YOZ.
Случай № 1 концентрирует внимание на плоскости YOZ = ς = γ, когда x0 = 0.
Положение 6. Полупространство полностью следует отдавать под контроль среднего зрительного центра O (0; 0; 0) в исключительных случаях, когда объекты невозможно полноценно различать и наблюдение за ними не имеет никакого смысла. Это ситуация, когда точка фокуса F(x0; y0; z0) принадлежит оси OX (F ϵ OX), то есть её ордината y0 = 0 и аппликата z0 = 0 равны нулю.
Случай № 2 показывает абсолютный приоритет среднего центра O над всеми точками БМП, когда y0 = 0 и z0 = 0.
Положение 7. Через центры L (‒d; 0; 0) и R (d; 0; 0) проходят зрительные плоскости λ (уравнение: x = ‒d) и ρ (уравнение: x = d) соответственно (L ϵ λ, R ϵ ρ) перпендикулярно координатным плоскостям XOZ и XOY, а также параллельно YOZ. Ареал полупространства, заключённый между плоскостями λ и ρ (|x| ≤ d), всегда будет находиться под влиянием среднего зрительного центра O (0; 0; 0), что находит отражение во всех ранее рассмотренных пяти случаях.
Положение 8. Если возникнет спорный случай контроля над какой-то LOR-областью B, когда на неё одновременно претендуют несколько различных зрительных центров среди множества, состоящего из правого зрительного центра R (d; 0; 0), левого центра L (‒d; 0; 0) и среднего - O (0; 0; 0), им следует отдать эту область B среднему центру O. Это справедливо, потому что зрительный приоритет начала координат - это равноправный обзор определённой части пространства обоими зрительными центрами L и R, согласно положению 27 БМП-подхода [1].
Например, в случае № 5 (см. рис. 3) при удовлетворении некоторой точки T (x; y; z) условиям x ‒ y ∙ x0 / y0 > 0 (лежит правее плоскости ς, значит R влияет на T) и x ‒ z ∙ x0 / z0 < 0 (находится слева от плоскости γ, поэтому по идее L влияет на T) её следует отдать под контроль среднему центру O.
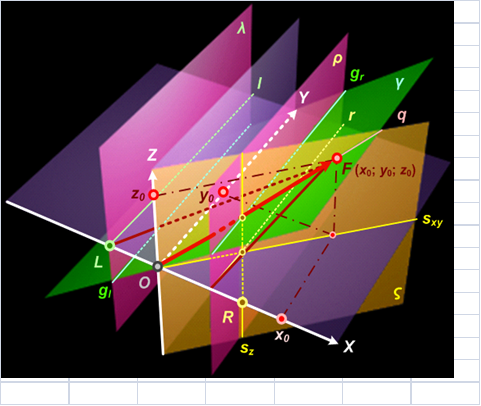
Рисунок 3. Точка фокуса F вне координатных плоскостей
Заключение
Полученное распределение LOR-областей используется в одной из самых важных прикладных задач аналитической геометрии на плоскости и в пространстве, решающихся для БМП, а именно - в задаче о поиске точки искажённой поверхности, по результатам которой выполняется параллельный перенос точки в БМП [2, 3].
На основе математической модели БМП были построены компьютерные модели с использованием ресурсов OpenGL (NIJANUS Glance 2.2 на языке программирования Delphi 6 и Glanceна языке программированияC# [6]). Разработанные программы моделируют искажение поверхности [4] в трёхмерном пространстве, параллельно переносимой относительно радиус-вектора фокуса в направлении начала координат при сохранении всех значений параметров данной поверхности в БМП. Программа Glance [6] была выполнена в рамках государственного контракта № 14.740.11.1149 «Математическая и компьютерная модель человеческого зрительного восприятия объектов» (шифр «2011-1.3.2-113-002») от 09 июня 2011.
Рецензенты:
Шестёркин А.Н., д.т.н., профессор, профессор кафедры «Вычислительная и прикладная математика», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Рязанский государственный радиотехнический университет», г. Рязань.
Антипов В.А., д.т.н., профессор, профессор кафедры «Информационно-измерительная и биомедицинская техника», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Рязанский государственный радиотехнический университет», г. Рязань.



