Введение
В настоящее время наиболее универсальным видом энергии стало электричество, обеспечивающее потребности практически всех отраслей. Рост промышленности требует значительного повышения уровня напряжений для передачи электроэнергии больших мощностей. Для уменьшения потерь при передаче электроэнергии на большие расстояния растут уровни напряжений. При этом возникает ряд проблем, связанных с возрастающим воздействием на окружающую среду и человека низкочастотных электрических полей, создаваемых как самими энергетическими установками, так и воздушными линиями электропередачи сверхвысокого и ультравысокого напряжения. В этой же связи в последнее время стали рассматриваться электрические поля, генерируемые электрифицированным транспортом, которые дают основной вклад в электрическое окружение плотно населенной городской среды.
Несмотря на большие наработки, сделанные как у нас в стране, так и за рубежом, и потребности промышленности в средствах и методах измерений, область электрических полей промышленной частоты на сегодняшний день оказалась не прикрытой ни средствами градуировки и поверки, ни стандартами, регламентирующими методики проведения измерений. Существующие методы и средства измерений напряженности электрического поля непригодны для измерения полей промышленной частоты вблизи и на поверхности электротехнического оборудования с требуемой точностью, в связи с внесением в электрическое поле значительных искажений. Это говорит о необходимости проведения исследовательских работ и обеспечения промышленности, науки, экологии и других областей знаний необходимыми средствами и методами поверки измерителей напряженности электрического поля промышленной частоты [6].
Предмет исследования
Известно, что вектор напряженности электрического поля многофазных энергетических систем промышленной частоты вращается в пространстве по эллипсу, проходя через максимальное и минимальное значения. При этом происходит изменение амплитуды и фазы вектора как во времени, так и в пространстве. В общем случае годограф радиус-вектора напряженности вращающегося электрического поля представляет собой эллипс (рисунок 1).
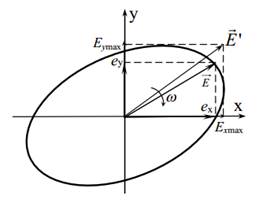
Рисунок 1. Годограф вектора напряженности электрического поля (общий случай)
Необходимо разработать установку для поверки средств измерения напряженности для электрических полей с эллиптической поляризацией, форма которой будет напоминать так называемую «беличью клетку», примерный внешний вид и конструкция устройства представлены на рисунке 2.
Рисунок 2. Конструкция устройства
Необходимо разработать и провести математические расчеты для построения установки, которая будет создавать электрическое поле с заданной величиной градиента составляющих напряженности. Особенностью такого поля является то, что вектор напряженности электрического поля изменяет не только свою амплитуду, но и направление.
Устройство представляет собой некоторое количество проводников, выполненных в форме трубок, расположенных параллельно друг другу, образуя цилиндрическую поверхность. Количество проводников будет кратно трем, по числу фаз переменного тока, подаваемого на трубчатые проводники. Общее количество проводников будет рассчитываться так, чтобы погрешность поля была в рамках требований эталонного электрического поля по государственной поверочной схеме.
Если, к примеру, будет использоваться «беличья клетка» с шестью проводниками, то на каждый из проводников будет подаваться переменный ток таким образом, чтобы каждый последующий проводник имел сдвиг по фазе на 120 градусов, т.е. в установке будет происходить последовательное чередование трех фаз, которые будут создавать вращающееся электрическое поле, в котором максимальное значение вектора напряженности электрического поля будет двигаться по спирали вдоль трубчатых проводников с электрическим током, делая полный оборот внутри устройства.
Габариты установки, в отличие от аналогов, будут значительно меньше, что позволит определять не только основную погрешность поверяемых приборов, но и дополнительные погрешности, например, от изменения температуры, поскольку установка не потребует создания большеобъемной камеры тепла и холода.
Расчет эллиптического электрического поля
Данная установка будет иметь трехмерное пространственное описание, поэтому и создаваемое ею поле также будет описываться в трехмерном пространстве.
Предположим, что электрическое поле, создаваемое данной установкой, может быть представлено в виде проекций на независимые координаты, тогда в декартовых координатах
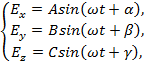(1)
где А, В, С – амплитудные значения напряженности переменного поля по осям x, y, z; α, β, γ – начальные значения фаз колебаний вдоль тех же осей, ω – циклическая частота колебания напряженности электрического поля, которая совпадает с частотой основной гармоники напряжения промышленной частоты ω=2πf=2π50=314 c–1.
Перейдем от параметрической формы записи к канонической.
Преобразуем систему (1), воспользовавшись формулами сложения к виду:
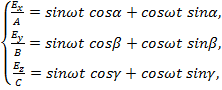(2)
Последовательно выразив cosωt и sinωt, избавимся от параметра ωt:
(3)
Произведем подстановку уравнения (3) в первое уравнение системы (2).
(4)
Произведем подстановку полученных выражений (3) и (4) в последнее уравнение системы (2) и преобразуем выражение:
Данное выражение представляет собой уравнение плоскости z', в которой расположена кривая, описываемая вектором напряженности электрического поля 
. Чтобы однозначно задать кривую, воспользуемся выражениями (3) и (4), а также основным тригонометрическим тождеством, и запишем:
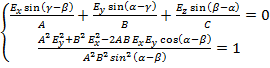(5)
Эта система уравнений однозначно задаёт эллипс, лежащий в плоскости z'. Для описания эллипсоида в параметрической форме записи необходимо использование двух параметров в системе, подобной (1).
Определим большую и малую полуоси эллипса. Для их нахождения достаточно исследовать функцию напряженности электрического поля или ее квадрата на экстремум. Учитывая систему уравнений (1), запишем:
В тех точках, в которых напряженность принимает наибольшее и наименьшее значения, выполняется условие
Определим значение ωt, при котором выполняется это условие:
+
Заранее известно, что чередование экстремальных значений в эллипсе происходит через интервальный период равный π/2.
;
Обозначим
.
Поскольку большая и малая полуоси эллипса смещены относительно друг друга на π/2, то можно записать выражения для полуосей эллипса:
;
.
Вид поляризации в плоскости поляризации z' электрического поля удобно характеризовать с помощью коэффициента поляризации:
,
где Еx' и Еy' – проекции напряженности электрического на ортогональные оси в плоскости поляризации z'; А', В' – амплитудные значения напряженноcти электрического поля, θ – разность между начальными фазами колебаний напряженности электрического поля на осях плоскости поляризации [1].
Если коэффициент поляризации является комплексным значением, то поле имеет эллиптическую поляризацию. При этом если коэффициент поляризации является мнимым числом, то оси эллипса совпадают с осями координат. Другим частным случаем может быть круговая поляризация, если z=±j, при условии равенства амплитуд А' и В'. Знак мнимой части определяет направление вращения вектора 
в плоскости поляризации: «плюс» соответствует правой поляризации (вращение вектора напряженности для наблюдателя, смотрящего в направлении прихода волны, происходит по часовой стрелке), «минус» – левой (вращение вектора происходит против часовой стрелки).
Для характеристики электрических и магнитных полей в течение одного периода логичнее использовать непосредственно интегральные характеристики параметров поляризованных полей, в нашем случае напряженности. В качестве таких характеристик могут быть приняты среднее значение напряженности за период
=
(6)
или действующее (среднеквадратичное) значение напряженности
(7)
Путем преобразования последнего выражения действующее значение определяется как
.
В выражениях (6) и (7) Е – напряженность электрического поля, определяемая по (5). Выше было показано, что эллиптическое поле можно привести к двум независимым координатам в плоскости поляризации волны, поэтому в дальнейшем продолжим рассмотрение поляризации электрической (магнитной) волн в этой плоскости, индексы «'» в дальнейшем будем опускать.
Интеграл выражения вида (6)
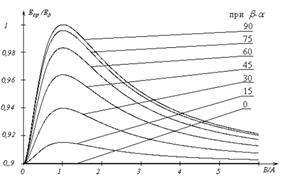
не может быть выражен через элементарные функции. Поэтому для вычисления средней напряженности используются формулы приближенного вычисления определенных интегралов на основе методов Ньютона – Котеса, Симпсона, Гаусса и др. [4, 7]. Произведем сравнение предложенных двух интервальных параметров, а именно – отношение среднего значения Eср к действующему значению напряженности эллиптического поля Ед в зависимости от параметров поляризации электрической волны соотношению амплитуд колебаний вектора напряженности на независимых координатах B/A и разности начальных фаз колебаний β–α, показанных на рисунке 3.
а)
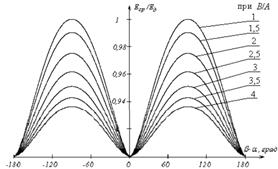б)
Рисунок 3. Зависимость Еср/Ед от параметров эллиптического поля:
а) от отношения амплитуд В/А, при β–α – const;
б) от разности начальных фаз β–α,при В/А- const.
Из представленных графиков следует, что при круговой поляризации среднее и действующее значения совпадают; наибольшее превышение действующего значения напряженности над средним значением в 1,09-1,11 раза наблюдается при линейной поляризации.
Использование действующих значений в качестве интегральной характеристики электрических и магнитных полей более целесообразно, поскольку оно учитывает не только постоянную составляющую поля, но и переменные составляющие.
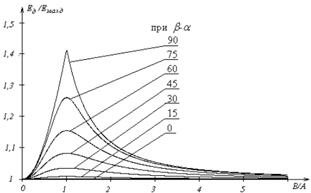
Сравним результаты расчета интегральной характеристики – напряженности электрического поля, рассчитанные по (7) Ед и напряженности электрического поля эффективного значения синусоиды, имеющей амплитуду, равную большей полуоси эллипса, описываемого вектором напряженности в расчетной точке Еmaxд, т. е. определим отношение Ед/Еmaxд. Сравнение произведем от вида и формы поляризации поля, а именно – по соотношению амплитуд колебаний вектора напряженности на независимых координатах B/A и разности начальных фаз колебаний β–α. Результаты сравнения показаны на рисунке 4[1].
а)
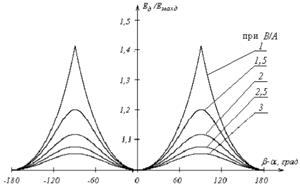б)
Рисунок 4. Зависимость Ед/Еmaxд от параметров эллиптического поля:
а) от отношения амплитуд B/A, при β–α – const;
б) от разности начальных фаз β–α, при В/А – const.
Анализируя полученные зависимости, можно сделать следующие выводы:
-
при линейной поляризации действующее и эффективное значения большей полуоси эллипса значения совпадают;
-
максимального расхождения значения Ед и Еmaxд достигают при круговой поляризации поля, при этом Ед/Еmaxд=
.
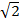Рецензенты:
Бубнов А.В., д.т.н., профессор, профессор кафедры «Электрическая техника» ФГБОУ ВПО «Омский государственный технический университет», г. Омск.
Никонов А.В., д.т.н., профессор, профессор кафедры «Автоматизированные системы обработки информации и управления» ФГБОУ ВПО «Омский государственный технический университет», г. Омск.