Введение
В качестве основного материала для строительства оснований и покрытий лесовозных автомобильных дорог (ЛАД), технических проездов, местных автомобильных дорог часто используют малопрочные местные каменные материалы, которые характеризуются незначительной прочностью. Они применяются в виде щебня различного зернового состава, при этом набор нормативной плотности конструктивного слоя из таких материалов сопровождается упаковкой, перемещением, измельчением частиц, а также взаимным заклиниванием с появлением значительных вертикальных и горизонтальных усилий.
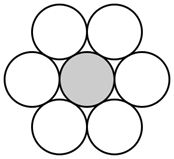
Чаще всего для слоев оснований и покрытий ЛАД характерен контактный тип структуры, при котором связь между частицами материала осуществляется непосредственно в местах контактов частиц.
Основной задачей данной работы является обобщение и анализ данных по изменению пористости и зернового состава малопрочных каменных материалов с уклоном на изучение формирования контактных сил между частицами, их взаимосвязью с уплотняющими нагрузками и измельчением материала с целью повышения транспортно-эксплуатационных качеств ЛАД.
Влияние контактных усилий на уплотнение
Обеспечение высоких транспортно-эксплуатационных показателей любой конструкции из щебня определяется постоянством структурных характеристик слоя, контактных усилий и зернового состава. А так как основой прочности щебеночных слоев дискретного типа является прочность каркаса, определяемая в первую очередь прочностью щебня, соблюдение этих условий при использовании малопрочных каменных материалов чрезвычайно важно. При этом современные конструктивные слои дорожных одежд ЛАД закладываются по формальным нормативным признакам без учета особенностей их уплотнения и вида используемого материала. Совсем не учитывается и изменение физико-механических свойств при уплотнении, что оказывает значительное влияние на транспортно-эксплуатационные качества ЛАД.
В механике грунтов считается, что лучший эффект при уплотнении достигается в тех случаях, когда контактные давления под рабочим органом катка близки к пределу прочности материала [3]. В условиях использования малопрочных каменных материалов это редко осуществимо и подбор подходящего катка по данному критерию достаточно проблематичен. Масса катка, ширина его вальца и сила вибраций должны находиться в определенном диапазоне, удовлетворяющем заданным условиям. Таким образом, целесообразно подобрать интенсивность и число приложений нагрузки для уже имеющейся техники. В этом случае необходимо учитывать не только контактные давления под рабочим органом при уплотнении, но и контактные усилия, возникающие между частицами в толще уплотняемого слоя.
Требуемая плотность щебеночных слоев может быть достигнута разными способами, при использовании различной техники, а соответственно и разных значениях уплотняющей нагрузки и времени проведения работ. Недостаток в величине нагрузки, требуемой для уплотнения материала, можно частично компенсировать числом её приложений, тогда как при завышенной её величине частицы материала необратимо деформируются и, как следствие, это приводит к снижению прочностных характеристик конструкции.
Изменение пористости и измельчение частиц
В качестве характеристики использованных материалов в таблице 1 приведены данные лабораторных испытаний, полученные в ходе моделирования процессов уплотнения каменных материалов [1], а также данные, полученные при исследовании изменения зернового состава щебня и коэффициентов сбега для разных режимов уплотнения и разной прочности исходного каменного материала [2].
Таблица 1. Пористость, дробимость и прочность частиц
|
Материал |
Изменение пористости |
Дробимость, % |
Прочность зерна, Мпа |
|
|
параметр a |
параметр b |
|||
|
Доломитовый щебень 1000 |
8,647 |
43,176 |
11,9 |
6,20 |
|
Гранитный щебень 800 |
8,485 |
42,33 |
23,6 |
2,64 |
|
Известняковый щебень 400 |
8,075 |
41,18 |
21 |
3,09 |
Примечание: Изменение пористости подчиняется логарифмической зависимости![]()
![]() , (1)
, (1)
где ![]() - прочность щебня при раздавливании в цилиндре, МПа;
- прочность щебня при раздавливании в цилиндре, МПа;
![]() - дробимость материала (потеря массы), %.
- дробимость материала (потеря массы), %.
Эта корреляционная зависимость между потерями массы и прочностью щебня при раздавливании в цилиндре была использована в целях исключения необходимости определения прочности зерен вручную и расчета контактных усилий между частицами на основе уже имеющихся исходных данных (паспорт материала).
Результаты измельчения каменного материала наиболее удачно удалось описать при помощи логарифмических функций, представленных в таблице 2.
Таблица 2. Изменение зернового состава
|
Материал |
Показатель |
Изменение зернового состава |
||||
|
<5 |
5-10 |
10-20 |
20-40 |
|||
|
Доломитовый щебень 1000 |
проходы катка: |
от 1 до 100 |
от 1 до 100 |
от 1 до 100 |
от 1 до 100 |
|
|
β0 |
7,722 |
2,157 |
0,821 |
−9,973 |
||
|
β1 |
0,786 |
0,036 |
0 |
0,037 |
||
|
β2 |
1,972 |
7,151 |
21,032 |
67,174 |
||
|
R2 |
0,984 |
0,976 |
0,972 |
0,993 |
||
|
Известняковый щебень 400 |
проходы катка: |
от 1 до 100 |
от 1 до 100 |
до 15 |
от 15 до 100 |
от 1 до 100 |
|
β0 |
11,596 |
1,633 |
3,57 |
−0,565 |
−12,094 |
|
|
β1 |
1,789 |
0,019 |
0,014 |
−14,745 |
0,111 |
|
|
β2 |
−6,646 |
6,481 |
15,131 |
23,166 |
73,509 |
|
|
R2 |
0,996 |
0,979 |
0,996 |
0,655 |
0,998 |
|
|
Гранитный щебень 800 |
проходы катка: |
от 1 до 100 |
от 1 до 100 |
до 10 |
от 10 до 100 |
от 1 до 100 |
|
β0 |
14,298 |
2,018 |
9,233 |
−3,599 |
−9,469 |
|
|
β1 |
7,525 |
0,188 |
0,309 |
−7,458 |
0,043 |
|
|
β2 |
−26,579 |
3,387 |
10,837 |
34,944 |
70,114 |
|
|
R2 |
0,974 |
0,994 |
0,998 |
0,989 |
0,997 |
|
Примечание: Данные применимы к логарифмической зависимости ![]() с параметрами β0, β1 и β2, которые отражают соответственно: количество и знак данных, горизонтальное смещение, вертикальное смещение.
с параметрами β0, β1 и β2, которые отражают соответственно: количество и знак данных, горизонтальное смещение, вертикальное смещение.
Степень измельчения материала использовалась для определения среднего значения радиуса частиц. Для щебня фракции 20-40 мм степень измельчения характеризуют фракции <10 мм.
![]() , (2)
, (2)
где ![]() - средний радиус частиц на i-ый проход катка, см;
- средний радиус частиц на i-ый проход катка, см;
![]() - средний радиус частиц до уплотнения, см;
- средний радиус частиц до уплотнения, см;
![]() - процент фракции 0-5 мм;
- процент фракции 0-5 мм;
![]() - процент фракции 5-10 мм.
- процент фракции 5-10 мм.
Напряжение в контактах частиц
Для того чтобы описать структуру уплотненного до определенной степени сыпучего материала, необходимо рассмотреть взаимодействие между его частицами. Это взаимодействие описывается напряжениями, возникающими между двумя частицами. Контактное напряжение измеряется в нормальных и касательных направлениях (рисунок 1). Нормальное напряжение контакта двух сфер радиусом R определяется как отношение прироста нормальной ограничивающей силы к укорочению радиуса сферы, а касательное - как отношение прироста касательной силы к смещению частиц относительно центра [8].
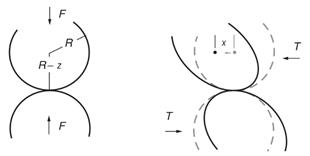
Рисунок 1. Нормальное и касательное напряжения в системе двух частиц.
![]() ;
; ![]() , (3)
, (3)
где ![]() - нормальное напряжение, МПа;
- нормальное напряжение, МПа;
![]() - касательное напряжение, МПа;
- касательное напряжение, МПа;
![]() - длина укорочения радиуса частицы, мм;
- длина укорочения радиуса частицы, мм;
![]() - смещение частицы относительно центра, мм.
- смещение частицы относительно центра, мм.
Эти свойства могут быть использованы вместе с контактным числом С, радиусом сферы R и пористостью φ для оценки напряженного состояния уплотняемого каменного материала.
Использование модели Герца-Миндлина
Модель Герца-Миндлина (Hertz-Mindlin) для прогнозирования модуля упругости в уплотненном сухом сыпучем материале основана на работе, проделанной Герцем (1882) [6] и Миндлином (1949) [9] о поведении упругих тел, находящихся в контакте. Предложенная авторами модель предполагает, что зерна одинаковых сфер упакованы случайным образом и содержит несколько допущений:
-
в решении для нормальных и касательных напряжений предполагается, что усилие сжатия влечет за собой возникновение касательной силы;
-
скольжение вдоль поверхности контакта между зернами отсутствует.
В ходе своих исследований Миндлиным установлено, что нормальные и касательные напряжения равны соответственно:
![]() ;
; ![]() , (4)
, (4)
где ![]() - модуль сдвига частицы, МПа;
- модуль сдвига частицы, МПа;
![]() - радиус зоны контакта, мм;
- радиус зоны контакта, мм;
![]() - коэффициент Пуассона.
- коэффициент Пуассона.
Согласно Герцу радиус зоны контакта ![]() и нормальное перемещение z, определяются следующими уравнениями:
и нормальное перемещение z, определяются следующими уравнениями:
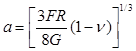 ;
; ![]() , (5)
, (5)
где ![]() - сдерживающая сила между частицы, МПа;
- сдерживающая сила между частицы, МПа;
![]() - радиус частицы, мм;
- радиус частицы, мм;
При давлении P, действующем на уплотненный материал, сдерживающая сила F, действующая между частицами будет равна:
![]() , (6)
, (6)
где ![]() - давление на образец материала, МПа;
- давление на образец материала, МПа;
![]() - радиус частицы, мм;
- радиус частицы, мм;
![]() - контактное число;
- контактное число;
![]() - пористость, %.
- пористость, %.
Большой практический интерес представляют значения контактных давлений, ниже которых требуемая плотность уплотняемого материала, даже при неограниченно большом числе проходов машин, уже не может быть достигнута. Для определения контактных усилий, возникающих между частицами в уплотняемом материале для каждого прохода рассчитано число контактов на одну частицу, учитывая текущую нагрузку, пористость (см. таблицу 1), средний радиус частицы (см. формула 2) и степень измельчения каменного материала (см. таблицу 2).
Контактное число
Контактное число – максимальное количество шаров одинакового радиуса, которые могут одновременно касаться одного такого же шара в n-мерном евклидовом пространстве (предполагается, что шары не проникают друг в друга). Вычисление контактного числа в общем случае до сих пор является нерешённой математической задачей [13].
|
n=2 |
n=3 |
|
|
|
|
|
|
Рисунок 2. Контактное число в двумерном (n=2) и трехмерном случаях (n=3).
Для частиц, упакованных случайным образом, это число определяется экспериментально путем подсчета контактов для подготовленных образцов [4, 11, 12]. В ходе таких исследований были сделаны некоторые важные выводы [11]:
-
контактное число увеличивается с уменьшением пористости образца, т.е. набором образцом плотности;
-
упакованные случайным образом частицы в виде идентичных шариков имеют среднее значение контактного числа, которое находится в пределах от ~6,9 (без уплотнения) до ~9,1 (при плотной упаковке);
-
значение контактного числа широко варьируется для каждого нового образца (от 4 до 12) и приведенное среднее значение не учитывает эту изменчивость.
Некоторые ученые приводят в своих работах критерий наиболее часто встречающихся значений пористости, который определен в пределах от 0,26 до 0,78 [7]. На рисунке 3 изображены обобщенные данные по изменению контактного числа частиц C в зависимости от пористости материала, без учета изменения формы и размеров частиц [4, 7, 10-12].
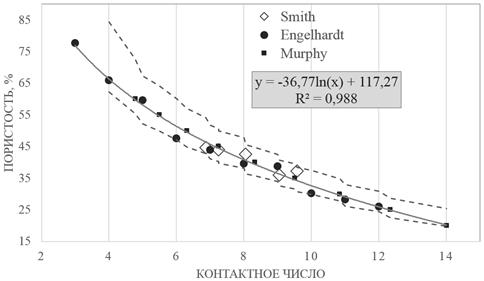
Рисунок 3. Зависимость контактного числа от пористости материала.
На рисунке 3 пунктиром отмечена область стандартного отклонения, описывающего пространственное изменение контактного числа по всей упаковке [11]. По некоторым данным эквивалентные контактные числа в произвольной упаковке частиц материала могут быть меньше, чем показано на рисунке 3, примерно на единицу [12].
В недавних исследованиях численного моделирования сыпучих сред [5] получена степенная зависимость между контактным числом и пористостью:
![]() , (7)
, (7)
где ![]() - контактное число на начальной стадии уплотнения (
- контактное число на начальной стадии уплотнения (![]() );
);
![]() - пористость материала на начальной стадии уплотнения (
- пористость материала на начальной стадии уплотнения (![]() );
);
![]() - пористость уплотненного материала (
- пористость уплотненного материала (![]() ).
).
Одним из источников неопределенности в экспериментальной оценке контактного числа также является трудность различия реальных контактов зерен и контактов вблизи их. Но при использовании в работе общих закономерностей изменения физико-механических свойств каменных материалов влияние этого фактора незначительно. Тем не менее, механические и упругие свойства в уплотненном каменном материале полностью определяются нагрузкой в контактах между частицами, которые они способны воспринимать без разрушения. Полученные результаты представлены в таблице 3 и на рисунке 4.
Таблица 3. Изменение сдерживающей силы и общей нагрузки на зерно
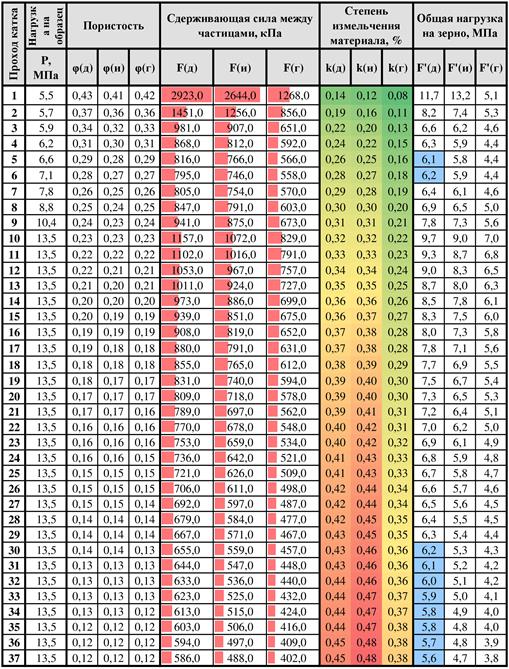
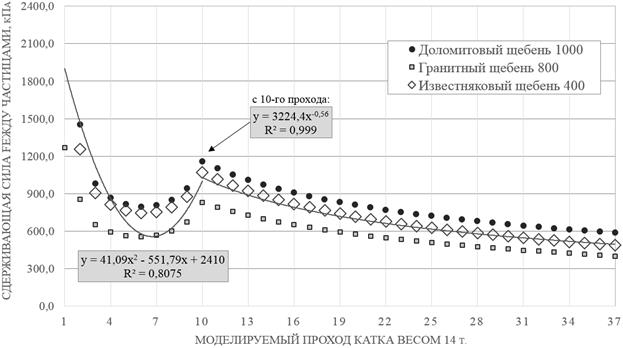
Рисунок 4. Зависимость сдерживающей силы между частицами и проходом катка.
Заключение
Ряд проведенных экспериментов и анализ полученных данных говорит о том, что контактные усилия в щебне при воздействии нагрузки уменьшаются с ростом числа контактов в единице объема. При этом изменение сдерживающей силы между двумя частицами каменного материала при разной прочности частиц имеет одинаковую тенденцию.
Полученные уравнения регрессии могут быть использованы для быстрого расчета напряженного состояния внутри уплотняемого щебеночного слоя на требуемый цикл уплотнения. Если при заданных условиях контактные усилия между частицами уплотняемого каменного материала превышают прочность щебенок, формирующих каркас уплотняемого слоя, велика вероятность того, что прочность конструкции уменьшится вследствие дальнейшего измельчения ее частиц.
Одной из важнейших задач при строительстве оснований и покрытий ЛАД является подбор уплотняющей техники и выбор режима уплотнения в зависимости от прочности используемого каменного материала или подбор оптимальной прочности самого материала таким образом, чтобы была обеспечена сохранность зерен даже при интенсивном уплотнении щебеночных слоев. Если величины контактных усилий в материале будут соизмеримы с его прочностью, то при уплотнении можно добиться постоянства зернового состава и в то же время обеспечить требуемую плотность конструктивного слоя. Сохранение постоянства структуры щебеночных оснований и покрытий на этапе строительства может повысить общие транспортно-эксплуатационные качества и обеспечить их высокие показатели на протяжении всего периода последующей эксплуатации ЛАД.
Рецензенты:
Силуков Ю.Д., д.т.н., профессор кафедры «Транспорта и дорожного строительства» Уральского государственного лесотехнического университета, г.Екатеринбург.
Кошкаров Е.В., д.э.н., к.т.н., старший научный сотрудник, «Научно-исследовательский центр» «УралГИПРОДОРНИИ» ОАО «ГИПРОДОРНИИ», г.Екатеринбург.