На современном этапе модернизации российского высшего профессионального образования (ВПО) в связи с введением федеральных государственных образовательных стандартов (ФГОС) третьего поколения весьма актуальными являются вопросы повышения качества обучения и контроля знаний, совершенствования методов оценки результатов обучения студентов [5, 7-10]. Согласно ФГОС ВПО, приоритетной задачей управления качеством образования выступает оценка качества освоения основных образовательных программ, включающая предварительную, текущую и итоговую формы контроля результатов образовательной деятельности студентов в рамках рейтинговой системы оценок с дальнейшим переводом их в экзаменационную (зачетную) оценку.
В данной работе (аналогично [2, 3] в системе заочного обучения) проведен многомерный статистический анализ результатов оценивания знаний по высшей математике (выборка 28 учебных групп) в объеме 1-го семестра студентов очной формы обучения Томского политехнического университета [6]. В рамках тернарного подхода (аналогично [1] для выборки вузов) рассмотрение проведено в системе 3-х показателей итоговый формы контроля (ЭКЗ) результатов образовательной деятельности студентов по 5-ти балльной шкале: ДОЛГ – доля сдавших ЭКЗ на «неуд» (в диапазоне [0; 2,5) по 5-ти балльной шкале) и не допущенных, УДОВЛ – доля сдавших ЭКЗ на «удовл» (в диапазоне [2,5; 3,5)) и КАЧ – доля сдавших ЭКЗ на «хор + отл» (в диапазоне [3,5; 5]). При этом ДОЛГ + УДОВЛ + КАЧ = 1 для любой учебной группы. Созданная таким образом в MS Excel база данных использовалась далее в пакете Statistica [4] для статистического анализа данных.
Тернарные координаты применяются при исследовании содержания 3-х компонентной (ДОЛГ, УДОВЛ и КАЧ) «смеси», при этом соотношение компонент изменяется от группы к группе на тернарной диаграмме рассеяния, но их сумма для всех групп остается постоянной, равной нормированной 1. Если построить 3-х компонентную «смесь» на обычной трехмерной диаграмме рассеяния, то окажется, что она образует треугольник в пространстве. Поэтому для отображения соотношений компонент достаточно просто построить треугольник на плоскости. Треугольные оси-медианы можно интерпретировать «тернарным» образом: тернарные переменные (ДОЛГ, УДОВЛ и КАЧ) убывают от наибольшего значения в соответствующей вершине треугольника вдоль осей-медиан до ноля в соответствующем основании медианы. Чтобы узнать координаты точки на тернарном графике, нужно просто "опустить" перпендикуляры из точки на оси-медианы. На рис. 1 представлена 4-х уровневая система координат, делящая исходный треугольник на 16 равносторонних маленьких. Например, с точки зрения (вершины) ДОЛГ: «верхний» уровень Д (ДОЛГ > 0,75), 3 уровня «выше среднего» Дд (0,50 < ДОЛГ < 0,75; КАЧ < 0,25; УДОВЛ < 0,25), Дк (0,50 < ДОЛГ < 0,75; 0,25 < КАЧ < 0,50; УДОВЛ < 0,25) или Ду (0,50 < ДОЛГ < 0,75; 0,25 < УДОВЛ < 0,50; КАЧ < 0,25); «средний» уровень Ц (0,25 < ДОЛГ < 0,50; 0,25 < КАЧ < 0,50; 0,25 < УДОВЛ < 0,50); уровень «ниже среднего» Цд (ДОЛГ < 0,25; 0,25 < КАЧ < 0,50; 0,25 < УДОВЛ < 0,50). Аналогично с точек зрения (вершин) КАЧ и УДОВЛ.
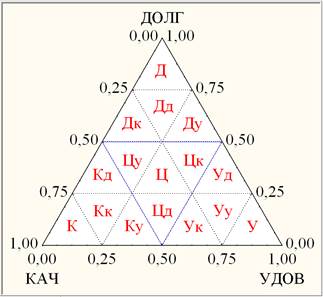
Рис. 1. 4-х уровневая тернарная система координат
Проведена древовидная кластеризация учебных групп студентов в 3-х мерном пространстве {ДОЛГ, УДОВЛ и КАЧ} дендрограммным методом (рис. 2).
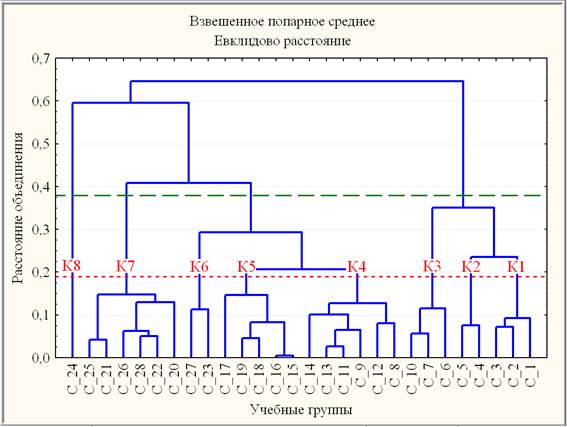
Рис. 2. Горизонтальная дендрограмма групп в пространстве {ДОЛГ, УДОВЛ и КАЧ}
В зависимости от выбора расстояния объединения можно получить соответствующее число кластеров. Так, например, уровню расстояния объединения, равного 0,19 (нижняя красная пунктирная горизонтальная прямая), соответствует 8 кластеров (К1- К8), уровню расстояния объединения, равного 0,38 (верхняя зеленая пунктирная горизонтальная прямая), – 4 блока кластера (К1+К2+К3, К4+К5+К6, К7, К8). Таким образом, выбор значения связующего расстояния позволяет проводить кластеризацию на любом уровне, то есть строить кластерную модель с любым наперед заданным числом кластеров. Заметим, что разбиение 28 групп на 8 кластеров обладает устойчивостью относительно вариации мер близости (расстояние Евклида, Чебышева, городских кварталов) и правил объединения двух кластеров (метод Варда, полной связи, попарного среднего).
Наряду с методом древовидной кластеризации, применяется также метод K-средних, проводящий классификацию объектов (групп) по заданному количеству кластеров. Алгоритм метода K-средних перемещает объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами.
Предлагается 8-и кластерная высококачественная модель групп, согласно λ-критерию Уилкса, высоко значимо (на уровне значимости р < 0,0005) различающая 8 кластеров учебных групп студентов по совокупности тернарных переменных (рис. 3).
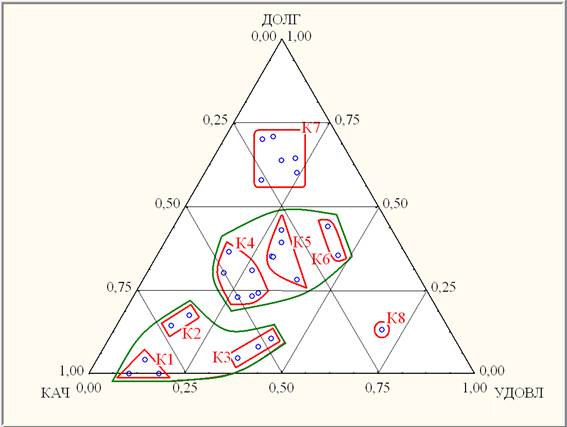
Рис. 3. Тернарная диаграмма рассеяния кластеров учебных групп в тернарном пространстве {ДОЛГ, УДОВЛ и КАЧ}
Взаимное расположение групп (синие кружочки), кластеров групп (красные объединения К1-8) и их блоков (зеленые объединения) на диаграмме рассеяния в тернарных переменных {ДОЛГ, УДОВЛ и КАЧ} (рис. 3) находится в точном соответствии с результатами кластеризация учебных групп студентов дендрограммным методом (рис. 2).
Значения параметрической F-статистики, полученные для каждой тернарной переменной, являются другим индикатором того, насколько хорошо проведена классификация. В рассматриваемом случае (табл. 1) F-критерий показывает, что для каждой тернарной переменной различие между кластерами высоко значимо (значимо на уровне p < 0,00005).
Таблица 1.
Результаты дисперсионного анализа качества 8-и кластерной модели учебных групп
|
|
Между SS |
сс |
Внутри SS |
сс |
F |
p |
|
КАЧ |
1,299 |
7 |
0,029 |
20 |
126,2 |
0,00000 |
|
УДОВЛ |
0,433 |
7 |
0,046 |
20 |
26,79 |
0,00000 |
|
ДОЛГ |
1,208 |
7 |
0,048 |
20 |
71,86 |
0,00000 |
Непараметрический критерий Краскела-Уоллиса смягчает уровень значимости различий кластеров до сильно значимого (на уровне значимости 0,0005< р < 0,005) по каждой тернарной переменной.
После получения результатов классификации рассчитываются средние значения тернарных показателей по каждому кластеру (рис. 4) для оценивания значимости их различий между собой.
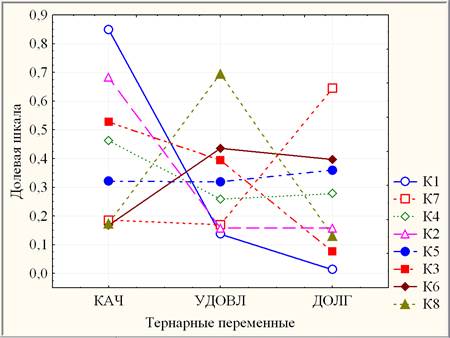
Рис. 4. Графики кластерных средних для каждого тернарного показателя
Согласно апостериорным критериям (Фишера, Шеффе, Тьюки) можно оформить результаты множественных сравнений кластерных средних в порядке их убывания для каждого тернарного показателя:
-
КАЧ: {К1}, { К2}, {К3, К4}, { К5}, {К7, К8, К6}так что К2 высоко значимо (на уровне значимости р < 0,0005) отличается от К1 или К3, а К5 сильно значимо (0,0005< р < 0,005) отличается от К4 или К7.
-
УДОВЛ : {К8}, {К6, К3, К5}, {К5, К4}, {К4, К7, К2, К1}, так что К8 и К6 различаются высоко значимо (р < 0,0005), а К6 и К4 или К5 и К1 различаются сильно значимо (0,0005< р < 0,005).
-
ДОЛГ: {К7}, {К6, К5, К4}, {К4, К2, К8}, {К2, К8, К3, К1}, так что К7 и К6 или К4 и К1 различаются сильно значимо (0,0005< р < 0,005), а К6 и К2 – статистически значимо (0,005 < p < 0,05).
Построенные последовательности неоднородных групп кластеров по каждому тернарному показателю находятся в согласии с результатами множественных сравнений по непараметрическому критерию Краскела-Уоллиса, смягчающему для КАЧ отличие К2 от К1 или К3 до слабо значимого (0,05< р < 0,10), а К5 от К4 или К7 до статистически значимого (0,005< р < 0,05); для УДОВЛ отличие К6 от К8 или К4 до слабо значимого (0,05< р < 0,10), а К5 от К1 до статистически значимого (0,005< р < 0,05); для ДОЛГ отличие К6 от К7 или К2 до слабо значимого (0,05< р < 0,10), а К4 от К1 до статистически значимого (0,005< р < 0,05).
Проведенная классификация детальным образом прописывает структуру тернарной 8-ти кластерной модели учебных групп, проводя в долевой шкале измерений различия 8-ти кластеров по совокупности тернарных показателей (рис. 5).
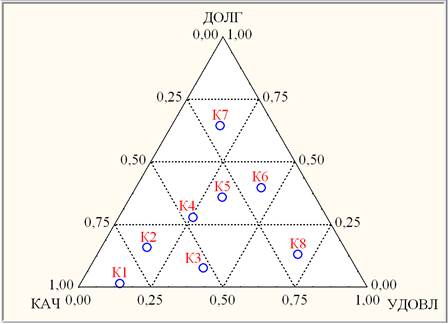
Рис. 5. Тернарная диаграмма рассеяния кластерных средних
Согласно рис. 5, с точки зрения (вершины) КАЧ, наилучшую качественную успеваемость имеют 3 группы кластера К1 (≈85% КАЧ и ≈1% ДОЛГ) уровня К (рис. 1), а наихудшую (»18% КАЧ) – три кластера, значимо различающиеся по ДОЛГ: 6 групп кластера К7 (≈64% ДОЛГ) уровня Дд, 2 группы кластера К6 (≈40% ДОЛГ) уровня Цк и 1 группа – кластер К8 (≈13% ДОЛГ) уровня Уу. Аналогичным образом можно характеризовать кластеры с других точек зрения (вершин). Так, например, с точки зрения (вершины) ДОЛГ, кластеры К1, К2, К3 и К8 – не просто имеющие ДОЛГ< 0,25, но значимо различающиеся по КАЧ и, согласно рис. 1, имеющие соответствующие уровни: К1 – уровень К, К2 – уровень Кк, К3 – уровень Ку и К8 – уровень Уу. К середнячкам во всех отношениях относятся 4 группы кластера К5 (≈32% КАЧ, ≈32% УДОВЛ и ≈36% ДОЛГ) уровня Ц.
Выводы
- В 3-х мерном тернарном пространстве {ДОЛГ, УДОВЛ и КАЧ} дендрограммным методом и методом K-средних получена высококачественная кластерная модель, распределяющая 28 групп студентов по 8-и кластерам и обладающая устойчивостью относительно вариации мер близости и правил объединения двух кластеров.
- Параметрический F-критерий показывает, что для каждой тернарной переменной различие между кластерами высоко значимо (значимо на уровне p < 0,00005), а непараметрический критерий Краскела-Уоллиса смягчает уровень значимости различий кластеров до сильно значимого (на уровне значимости 0,0005< р < 0,005).
- В рамках параметрического и непараметрического дисперсионного анализа выделены для каждого тернарного показателя однородные (различающиеся незначимо) группы кластеров.
- Результаты тернарной кластеризации (по совокупности показателей) результатов оценивания знаний могут быть учтены в процессе обучения для оценки качества образования и контроля знаний.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.



