Введение
Нефтяная промышленность – стратегически важная отрасль России, и от её состояния зависит дальнейший экономический рост страны. Нефть является не только топливом, а и важнейшим источником химического сырья для многих смежных отраслей народного хозяйства [2].
Надежность и бесперебойность поставки нефти потребителям через нефтеперевалочные комплексы (резервуарные парки) являются основными требованиями, предъявляемыми к системам нефтеснабжения. Соблюдение и выполнение указанных требований в полном объеме возможно лишь при высоком уровне автоматизации технологического процесса перекачки нефти.
Цель исследования
Проведение синтеза оптимального управления резервуаром с управляемыми подачей и сливом нефти с целью повышения эффективности работы резервуарного парка.
Методы исследования
Методом исследования технологического процесса перекачки нефти через резервуарный парк выступает метод математического моделирования, который заключается в установлении зависимостей между входными и выходными параметрами рассматриваемого объекта (резервуарного парка).
Рассматриваемая в статье математическая модель описывает процесс распределения и перекачки нефти, поступающей в резервуар из нефтепроводной системы, и призвана разрешить задачу создания системы оптимального управления резервуарным парком.
Для того чтобы представить рассматриваемый технологический процесс перекачки нефти как процесс управления, необходимо разбить переменные на группы.
Входные переменные:
X1 – количество поступившей из нефтепровода нефти;
Х2 – температура поступившей нефти;
Х3 – качественный состав поступившей нефти.
Управляющие переменные:
U1 – давление приходящей нефти;
U2 – давление расходуемой нефти.
Переменные, характеризующие условие протекания технологического процесса перекачки:
Выходные переменные:
Y1 – верхний уровень нефти в резервуаре;
Y2 – нижний уровень нефти в резервуаре;
Y3 – потеря нефти с «дыханиями» резервуара.
Возмущающими воздействиями являются:
- состав нефти;
- состояние насосов;
- колебания температуры окружающей среды;
- и т. д.
Следует отметить тот факт, что некоторые переменные рассматриваемого технологического процесса не могут быть определены с достаточной степенью точности, ввиду отсутствия соответствующих контрольно-измерительных приборов. К примеру, практически не предоставляется возможным поддерживать непрерывный процесс мониторинга за состоянием резервуаров или измерять величину потерь нефти с так называемыми «дыханиями» резервуара. Эти переменные препятствуют оценке состояния процесса и ухудшают оперативное управление им – рассматриваемый объект относится к классу объектов с неполной информацией. Необходимо также учесть тот факт, что рассматриваемый технологический процесс резервуарного парка нестационарен ввиду непостоянства факторов, его характеризующих (налипание парафина на приемно-раздаточные патрубки, непостоянство содержания воды в нефти и др.).
Рассмотрим управление цилиндрическим резервуаром с управляемыми подачей и сливом нефти. Запишем систему уравнений для объекта [1]:
![]() ;
;
![]() ; (1)
; (1)
![]() ,
,
где ![]() – расход жидкости в подающем трубопроводе;
– расход жидкости в подающем трубопроводе; ![]() – положение клапана на сливном трубопроводе;
– положение клапана на сливном трубопроводе; ![]() – высота уровня; ограничения следующего вида:
– высота уровня; ограничения следующего вида: ![]() ;b1, b2, k3 – коэффициенты пропорциональности. Принимаем
;b1, b2, k3 – коэффициенты пропорциональности. Принимаем![]() .
.
Множество стационарных состояний задается поверхностью ![]() . Необходимо исследовать оптимальное управление, переводящее на множество стационарных состояний координаты из любой точки пространства.
. Необходимо исследовать оптимальное управление, переводящее на множество стационарных состояний координаты из любой точки пространства.
Исследуем условия общности положения для данного объекта. Управления u1 и u2 независимы, то проверку условия общности положения проводим отдельно по каждому. Запишем систему (1) в векторной форме:
![]()
где
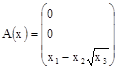 ;
;
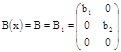 ;
;
![]() .
.
Исследуем условия общности положения для ![]() , когда [5]
, когда [5]
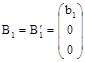
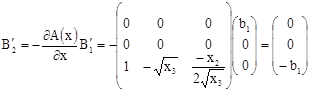 ;
;
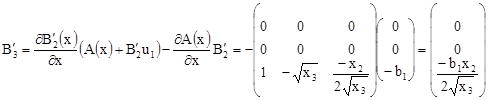 .
.
Составляем матрицу D"3 = (B`1,В`2,В`3):
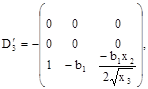
![]() . (2)
. (2)
Объект не управляем в R3, но управляем в R2{х2,х3}, т.к. ранг матрицы D"3 равен двум. Имеется и особая линия – ось х3, которая является пересечением особых плоскостей x1 = 0 и x2 = 0. На оси x3 стационарная поверхность имеет минимум, но особые плоскости имеют одновременно и ограничения, поэтому исследование особых управлений и особых траекторий можно не проводить.
Исследуем условия общности положения одновременно для двух управлений u1 и u2. Матрица D"3 = (B1,B2,B3) будет иметь следующий вид:
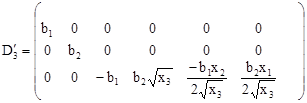 . (3)
. (3)
Ранг матрицы D"3 равен трем, и объект управляем в R3 = (х1,х2,х3} . В пространстве R3 также имеются особые плоскости х1= 0, х2= 0 и особая линия – ось х2, которые совпадают с ограничениями.
Для нахождения оптимальных управлений применим принцип максимума. Составим функцию Н и систему уравнений для функций ![]() :
:
![]() ;
;
![]() (4)
(4)
![]()
![]()
Максимум функции Н достигается при следующем условии:
![]() ; (5)
; (5)
Закон управления – релейный. Количество интервалов управления определяется нулями функций![]() и
и ![]() . Найдем решения для
. Найдем решения для ![]() и
и ![]() [6].
[6].
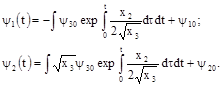 (6)
(6)
Функции ![]() и
и ![]() могут не более одного раза менять знак, поэтому управления и
могут не более одного раза менять знак, поэтому управления и ![]() и
и![]() содержат не более двух интервалов. Для заданных граничных условий первые интервалы должны быть противоположного знака. Утверждение о количестве перемен знака бесспорно для функции
содержат не более двух интервалов. Для заданных граничных условий первые интервалы должны быть противоположного знака. Утверждение о количестве перемен знака бесспорно для функции ![]() .
.
Функция ![]() содержит координату х3, от поведения которой может зависеть число перемены знака. В данном случае в процессе управления координата х3 знака не меняет в силу безусловных ограничений. В нуль она обращается только в единственной стационарной линии х1 = х3 = 0, то есть на оси х2. Поэтому в процессе управления х3 не может менять знака. Тогда функция
содержит координату х3, от поведения которой может зависеть число перемены знака. В данном случае в процессе управления координата х3 знака не меняет в силу безусловных ограничений. В нуль она обращается только в единственной стационарной линии х1 = х3 = 0, то есть на оси х2. Поэтому в процессе управления х3 не может менять знака. Тогда функция ![]() не более одного раза меняет знак.
не более одного раза меняет знак.
Анализ оптимальных управлений дает следующие решения задачи:
![]() и
и ![]() . Управление
. Управление ![]() – релейное, имеет не более двух интервалов, осуществляется подачей нефти в резервуар.
– релейное, имеет не более двух интервалов, осуществляется подачей нефти в резервуар.
![]() и
и ![]() . Управление
. Управление ![]() – релейное, имеет не более двух интервалов, реализуется путем слива нефти из резервуара.
– релейное, имеет не более двух интервалов, реализуется путем слива нефти из резервуара.
![]() и
и ![]() . Управления
. Управления ![]() и
и ![]() – релейные, имеют не более двух интервалов, реализуется как подачей нефти в резервуар, так и сливом ее из резервуара.
– релейные, имеют не более двух интервалов, реализуется как подачей нефти в резервуар, так и сливом ее из резервуара.
Из вышесказанного делаем вывод, что решение оптимальной задачи не единственное. Получены три варианта оптимальных управлений, и каждый из них удовлетворяет принципу максимума. Из полученных управлений следует выбрать такое, которое даст при данных граничных условиях минимальное время [4].
Рассмотрим управление для граничных условий, когда начальные условия заданы в нуле х1=х2=х3=0, а конечные условия находятся на множестве стационарных состояний. Необходимо, следовательно, объект из нуля перевести на множество стационарных состояний.
Представим граничные условия в следующем виде:
х10=х20=х30=0; (клапаны закрыты и резервуар пуст)
х1n, х2n, х3n, (причем должно выполняться соотношение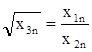 ).
).
Последовательность управлений должна иметь вид:
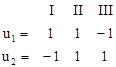
Но координата х2 не может принимать отрицательных значений в силу безусловного ограничения (сливной клапан закрыт).
Поэтому интервал ![]() заменяется интервалом
заменяется интервалом ![]() .
.
Последовательность управлений с учетом безусловного ограничения на х2 имеет вид:
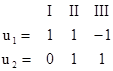
Записываем системы уравнений и их решения на отдельных интервалах.
Первый интервал равен:
![]() ,
,
![]() , (7)
, (7)
![]() ,
,
так как х2=0.
Решения для х1 и х3 следующие:
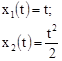 (8)
(8)
Второй интервал равен:
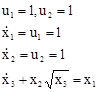 (9)
(9)
Решения для х1(t) и х2(t) имеют вид:
![]() (10)
(10)
Подставляем полученные решения для х1(t) и х2(t) в третье уравнение, получим:
![]() (11)
(11)
Третий интервал будет равен:
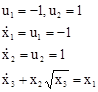 (12)
(12)
Решения для х1(t) и х2(t) будут иметь следующий вид:
![]() (13)
(13)
Подставляем полученные решения х1(t) и х2(t) в третье уравнение:
![]() (14)
(14)
Из решений данного управления следует определить время оптимального процесса Т, момент t2 включения ![]() и момент t1 переключения
и момент t1 переключения ![]() . Аналитически найти t1, t2 и Т не представляется возможным, поэтому они определяются приближенно из условия прохождения оптимальной траектории через конечные точки х1n, х2n, х3n[3].
. Аналитически найти t1, t2 и Т не представляется возможным, поэтому они определяются приближенно из условия прохождения оптимальной траектории через конечные точки х1n, х2n, х3n[3].
С физической точки зрения объяснение оптимального управления весьма просто – при закрытом сливном клапане уровень в резервуаре поднимается с наибольшей скоростью.
Допустим, что количество нефти, перекачиваемой без системы автоматизации, составляет 29200 у.т/год со стоимостью перекачки 292000 у.е./год.; количество перекачиваемой нефти с оборудованной системой автоматизации составляет 36500 у.т/год со стоимостью перекачки 255500 у.е./год.
Рассчитаем экономический эффект оснащения резервуарного парка (РП) системой автоматизации на основе AdvantController 450 компании по автоматизации технологий «ABB». Результаты расчета сведем в таблицу 1.
Таблица 1
|
|
РП не оснащен АСУ |
РП оснащен АСУ |
|
Количество перекачиваемой нефти, у.т./год |
29200 |
36500 |
|
Стоимость перекачки нефти, у.е./год |
292000 |
255500 |
|
Единоразовые инвестиции в АСУ, у.е. |
0 |
350000 |
|
Эксплуатационные затраты, у.е. |
0 |
20000 |
В результате проведённых расчетов на основе данных таблицы 1 период окупаемости инвестиций в автоматизацию РП составляет ~ 2,5 года [7].
Выводы
1. Резервуарный парк, в котором функционирует система автоматизации на основе синтеза оптимального управления резервуаром, увеличивает его пропускную способность, т. е. через парк перекачивается в сутки больший объем нефти, чем при отсутствии системы.
2. Автоматизация резервуарного парка на основе синтеза оптимального управления резервуаром с управляемыми подачей и сливом нефти экономически целесообразна.
Рецензенты:
Веселов О.В., д.т.н., профессор кафедры мехатроники и электронных систем автомобилей ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Сысоев С.Н., д.т.н., профессор кафедры автоматизации технологических процессов, ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» г. Владимир.



