Введение
Единственная значимая основа для построения решений различного класса задач – это энергетические описания сложных систем, параметры которых приняты за порождающие инварианты. Баланс энергии и серьезная энергетическая методология должны быть построены не на топологической или диакоптической комбинаторике, не на анализе токов и напряжений как единственно полезных параметрах, а на энергиях или мощностях [3].
Построению такой теории в настоящее время способствуют как уровень математики, так и роль компьютеризации, сделавшей фундаментальные методы доступными и, как следствие, целесообразными для прикладной и педагогической разработки [2].
Целью данной статьи является формирование новой методики решения энергетических задач теоретической электротехники, подключающей все современные методы компьютеризации.
Методика
При преобразованиях электрических цепей, как известно, мощность не является инвариантом. В свою очередь это может вызывать некоторые неудобства при рассмотрении энергетической задачи, поэтому в работе предлагаются методы преобразования цепей, инвариантами которых является мощность [4].
В качестве примера приведены два новых метода для инженерной электротехники с более конструктивных позиций. Рассмотрим последовательность примеров, наглядно иллюстрирующих фундаментальную роль свойств цепей в формировании их состояний.
Экспериментальная часть
Спектральный метод
Суть спектрального метода – в том, что любая физическая система находится лишь в состояниях, формируемых линейной комбинацией собственных функций этой системы.
Рассмотрим применение спектрального метода на примере тривиальной схемы.
Пусть задана связная цепь (рис. 1) с контурными токами ![]() ,
, ![]() и контурными ЭДС
и контурными ЭДС ![]() ,
, ![]() . Значения сопротивлений
. Значения сопротивлений ![]() Ом, источников ЭДС
Ом, источников ЭДС ![]() В.
В.
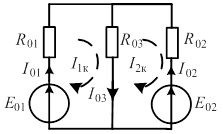
Рис. 1. Схема цепи с контурными токами
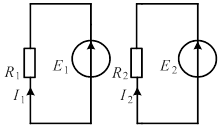
Рис. 2. Схема цепи двух несвязанных контуров
Убеждаемся, что баланс выполняется:
P0П ![]() Вт;
Вт;
P0И ![]() Вт; (1)
Вт; (1)
P0П = P0И = P0;
где P0П – мощность потребителей, P0И – мощность источников, ![]() = 0,167 А,
= 0,167 А, ![]() = -0.389 А.
= -0.389 А.
Далее необходимо расщепить связную схему до двух простых несвязанных контуров (рис. 2) и найти новые сопротивления и источники ЭДС с помощью специальных программ пакета MathCAD:
![]() Ом;
Ом;
![]() ;
; ![]() ; (2)
; (2)
![]() В;
В; ![]() А;
А;
где 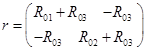 – матрица контурных сопротивлений,
– матрица контурных сопротивлений, ![]() – собственные числа,
– собственные числа, ![]() – собственные вектора,
– собственные вектора, ![]() – новые источники ЭДС, I – токи ветвей.
– новые источники ЭДС, I – токи ветвей.
Здесь (2) после преобразований новые сопротивления являются собственными числами, а соответствующие столбцы ортогональной матрицы – собственными векторами матрицы сопротивлений связной схемы. Собственные вектора позволяют перейти от векторных уравнений к скалярным уравнениям. Затем необходимо найти токи и составить баланс мощностей по известным формулам и проверить инвариантность мощности по (1):
PП ![]() Вт;
Вт;
PИ ![]() Вт;
Вт;
PП = PИ = P0.
Убеждаемся, что баланс мощности выполняется.
Для наглядности на рисунке 3 приведена очевидная геометрическая интерпретация метода.
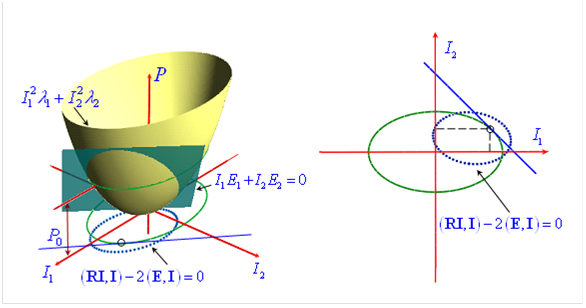
Рис. 3. Геометрическая интерпретация.
В точке касания имеет место баланс мощностей. Вся возникающая на плоскости геометрическая картина является горизонтальной проекцией взаимопересечений трёхмерных поверхностей в трёхмерном пространстве, по вертикальной оси которого откладываются мощности, а горизонтальной системой координат остаётся плоскость токов. Точка состояния цепи есть нижняя точка поверхности (рис. 3) – точка минимума мощности, выделяющейся на резисторах (мощности потерь).
Определяющим элементом всей описанной выше картины является обязательный компонент любого экстремального толкования физических процессов – мощностной или энергетический инвариант, фундаментальный для данного семейства систем. Его существование делает тривиальной логику формирования конкретной точки состояния системы в любой системе координат. Таким инвариантом в данном случае является неизменный по форме эллиптический параболоид мощности потерь данного порождающего набора резисторов ![]() .
.
В рассмотренном примере из группы унитарных преобразований оказалось достаточным использование ортогонального преобразования, соответствующего повороту эллиптического параболоида потерь в однородном координатном базисе [7].
Метод минимизации энергии
Метод минимизации энергии – один из альтернативных методов решения задач электротехники. Любая физическая система стремится к минимуму энергии [5].
Если записать функционал энергии для электротехнической системы с последующей его минимизацией, то можно получить уравнения для интересующих нас обобщенных координат [6].
В зависимости от того, что выбирается в качестве обобщенных координат, функционал S записывается по-разному.
Если в качестве обобщенных координат выбираются контурные токи (рис. 1), функционал мощности может быть записан в зависимости от контурных токов:
![]() .
.
Минимизировать функционал ![]() можно, взяв частную производную по
можно, взяв частную производную по ![]() и
и ![]() и приравняв ее к нулю. Полученная система и даст нам интересующие нас контурные токи:
и приравняв ее к нулю. Полученная система и даст нам интересующие нас контурные токи:
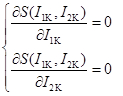 (3)
(3)
Минимизировать функционал возможно так же и с помощью программы Minimize программно-интегрированной среды MathCAD:
Minimize(S,![]() ,
,![]() ) , (4)
) , (4)
где ![]() = 0,167 А,
= 0,167 А, ![]() = -0.389 А.
= -0.389 А.
Ниже продемонстрирована универсальность метода на примере нелинейной цепи с двумя источниками ЭДС (рис. 4).
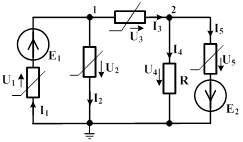
Рис. 4. Нелинейная цепь.
Значения источников ЭДС ![]() В.
В.
Зависимость токов ветвей от напряжений ветвей:
![]() .
.
Мощность ветвей:
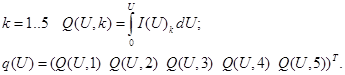
Функционал мощности в зависимости от потенциалов записан ниже, где в качестве обобщенных координатах выбраны потенциалы:
![]() . (5)
. (5)
Минимизация функционала (5) осуществлена по (3). Полученная система даст интересующие потенциалы:
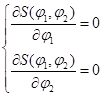 ,
,
где ![]() = 5,981 В,
= 5,981 В, ![]() = 4,271 В.
= 4,271 В.
Минимизировать функционал возможно так же и с помощью программы Minimize (4).
Результаты
Реализация данных методов является идеалом с точки зрения электромагнитной совместимости устройств, включая совместимость по симметрии сети, из-за отсутствия в этом случае “набросов” мощности, идущей обычно как на формирование сетевой, так и высокочастотной помех [8]. Представляется весьма высокой и учебно-методологическая ценность предлагаемого подхода, раскрывающая электротехническое содержание собственных векторов и собственных чисел матриц описаний состояний электротехнических устройств.
Отметим основные достоинства использованных выше методов:
- позволяют оптимизировать электротехническую систему;
- раскрывают физическую сущность системы;
- хороши для синтеза электротехнических схем;
- позволяют получить схему с наперед заданными свойствами.
Это актуально в задачах электроэнергетики при рассмотрении электромеханических систем. Также выше описанные методы дают возможность не только определять множества цепей с постоянной мощностью, но и позволяют преобразовать векторно-матричные уравнения электрических цепей в скалярные уравнения [1].
Рецензенты:
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Лукутин Б.В., д.т.н., заведующий кафедрой ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.



