Морские нефтегазовые сооружения подвергаются воздействию различных факторов, влияющих на их температурное состояние. Главным фактором, влияющим на формирование температуры конструктивных элементов морских нефтегазовых сооружений, является солнечное излучение. Однако, помимо солнечного излучения, следует учитывать такие факторы, как степень прозрачности атмосферы, ветровое воздействие, условия теплоотвода в окружающую среду и другие факторы, о которых будет сказано в дальнейшем [1-12]. Наиболее сильно солнечному воздействию подвержены морские стационарные платформы (МСП) [1; 5-12], расположенные на незащищенных от солнечного воздействия участках в открытом море [1; 5-12]. Замеры, проведенные автором на МСП, расположенных на шельфе Черного моря, показали, что при определенных условиях температура элементов морских стационарных платформ может достигать до +70 градусов Цельсия. Теоретически возможно и превышение этого значения [1; 5-12]. Как известно, изменение температуры в сечениях элементов МСП создает в них переменные напряжения, которые в свою очередь негативно влияют на их усталостную долговечность [5-12] и при определенных условиях способствуют развитию такого опасного дефекта, как усталостные трещины. В отличие от нефтегазопроводов, в которых температурное состояние определяется в первую очередь температурой перекачиваемых продуктов, температурный режим опорных блоков морских стационарных платформ определяется различными условиями окружающей среды, главным из которых является интенсивность солнечного излучения [5-12]. Как известно, солнце находится от Земли на расстоянии примерно 150 млн км [3; 4]. Поскольку продольная ось Земли движется вокруг Солнца наклонно по эллиптической орбите, солнечное излучение, падающее па земную поверхность, меняется по временам года. Полная мощность излучения, которое падает на поверхность площадью 1 м2, помещенную вне атмосферы Земли (выше 150 км), называется солнечной постоянной, которая равняется 1395 Вт/м2 [3; 4]. Однако интенсивность солнечного излучения зависит также от географического положения МСП, времени года, времени суток, погодных условий, условий теплоотдачи в окружающую среду и др. Поэтому решение задачи определения воздействия солнечного излучения на конструктивные элементы МСП будет разбито автором на следующие этапы: 1) определение плотности теплового потока, полученного конструктивными элементами (КЭ) МСП от суммарного солнечного излучения; 2) оценка влияния температуры окружающей среды и ее динамики на формирование температуры конструктивных элементов МСП; 3) исследование распространения температурного поля по сечениям КЭ МСП. При прохождении солнечного излучения через земную атмосферу его интенсивность уменьшается вследствие действия [3; 4]: поглощения молекулами кислорода, озона, углекислого газа, водяного пара, пыли и слоями облаков (в целом атмосферой поглощается 17...25% солнечного излучения); рассеяния молекулами сухого воздуха и пылью; отражения слоями облаков. Излучение, достигающее земной поверхности, состоит из прямого и диффузионного. Прямым излучением называется поступающее от Солнца излучение без изменения его направления. Диффузным (или рассеянным) излучением называется солнечное излучение после изменения его направления вследствие отражения и рассеяния атмосферой. В пасмурную погоду преобладает диффузное излучение. Суммарный поток солнечного излучения, получаемый горизонтальной поверхностью на Земле, называется инсоляцией. Введем следующие понятия, необходимые для расчета (табл. 1).
Таблица 1.
Характеристика значений, характеризующих интенсивность солнечного излучения в условиях морского нефтегазового месторождения
|
Наименование |
Обозначение |
Описание |
|
Угол падения прямого солнечного излучения (луча) |
Θ |
Угол между направлением излучения на любую поверхность и нормалью к этой поверхности. Измеряется в радианах |
|
Склонение |
δ |
Угловое положение Солнца в солнечный полдень относительно плоскости экватора (значение положительно для Северного полушария. Измеряется в радианах) |
|
Азимутальный угол плоскости |
γ |
Отклонение нормали к поверхности от местного меридиана (за начало отсчета принимается южное направление, отклонение к востоку считается положительным, к западу - отрицательным) |
|
Высота Солнца |
α |
Угол между направлением прямого солнечного излучения и горизонтальной проекцией солнечного луча. Измеряется в радианах |
|
Часовой угол |
ω |
Угол, который определяет угловое смещение Солнца в течение суток. Один час соответствует π/12 рад или 15 град углового смещения. В полдень часовой угол равен нулю. Значения часового угла до полудня считаются положительными, после полудня - отрицательными. Измеряется в радианах |
При вычислении плотности теплового потока солнечного излучения, или, иначе говоря, радиации, поступающей на какую-либо наклонную поверхность, составляют уравнение радиационного баланса в виде [3; 4]:
![]() ), (1)
), (1)
где Qнакл — суммарная плотность теплового потока солнечной радиации, падающей на наклонную поверхность конструктивного элемента МСП, Вт/м2; Sнакл — плотность теплового потока прямого солнечного излучения, падающего на наклонную поверхность конструктивного элемента МСП, Вт/м2; Dнакл — плотность теплового потока рассеянной солнечной энергии, падающей на наклонную поверхность конструктивного элемента МСП, Вт/м2; К — поправочный коэффициент, учитывающий отраженный от поверхности морской воды тепловой поток. Значение Sнакл находят по зависимости [3; 4]
![]() (2)
(2)
где Sорт — прямое солнечное излучение на ортогональную лучам поверхность, Вт/м2.
Значение Sорт находят по формуле Кастрова [3; 4]:
![]() (3)
(3)
где S0 — солнечная постоянная, равная 1395 Вт/м2; с — величина, характеризующая степень прозрачности атмосферы. Характеристика коэффициента с и его численные значения приведены в таблице 2.
Таблица 2
Характеристика коэффициента с и его численные значения
|
|
Степень прозрачности атмосферы |
||||||
|
Идеальная |
Высокая |
Повышенная |
Нормальная |
Пониженная |
Низкая |
Сверхнизкая |
|
|
Численное значение коэффициента, с |
0,13 |
0,27 |
0,34 |
0,43 |
0,54 |
0,67 |
0,91 |
Произведем расчет величины плотности теплового потока от прямого солнечного излучения на ортогональную лучам поверхность при различных высотах положения солнца α и степени прозрачности атмосферы с.
Таблица 3
Значения величины плотности теплового потока от прямого солнечного излучения Sорт, Вт/м2
|
Степень прозрачности атмосферы, с |
Высота солнца α в градусах |
||||||||||
|
7 |
10 |
15 |
20 |
25 |
30 |
40 |
50 |
60 |
75 |
90 |
|
|
Высота солнца α в радианах |
|||||||||||
|
0,12 |
0,17 |
0,26 |
0,35 |
0,44 |
0,52 |
0,7 |
0,87 |
1,05 |
1,31 |
1,57 |
|
|
0,91 |
162,18 |
218,69 |
307,29 |
381,79 |
444,77 |
492,68 |
578,22 |
636,82 |
680,79 |
718,39 |
730,37 |
|
0,67 |
211,47 |
281,24 |
386,84 |
472,25 |
542,17 |
594,02 |
683,82 |
743,37 |
787,07 |
823,76 |
835,33 |
|
0,54 |
253,14 |
332,79 |
449,93 |
541,79 |
615,14 |
668,49 |
758,88 |
817,46 |
859,77 |
894,86 |
905,84 |
|
0,43 |
303,79 |
393,89 |
521,96 |
618,89 |
694,19 |
747,83 |
836,59 |
892,75 |
932,66 |
965,36 |
975,52 |
|
0,34 |
363,27 |
463,51 |
600,63 |
700,46 |
775,76 |
828,25 |
913,09 |
965,51 |
1002,18 |
1031,88 |
1041,04 |
|
0,27 |
428,52 |
537,38 |
680,40 |
780,46 |
853,79 |
903,85 |
983,01 |
1030,85 |
1063,86 |
1090,31 |
1098,43 |
|
0,13 |
668,76 |
788,85 |
926,49 |
1011,51 |
1068,80 |
1105,71 |
1160,76 |
1192,22 |
1213,18 |
1229,56 |
1234,51 |
Следующим шагом необходимо вычислить косинус угла падения прямого солнечного излучения на поверхность конструктивного элемента МСП, который определяют по следующей формуле [3; 4]:
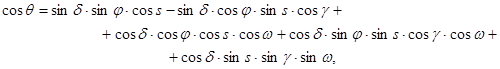 (4)
(4)
где φ — географическая широта местности, рад; δ — склонение Солнца, рад; s — угол наклона КЭ МСП к горизонту, рад.
С учетом анализа значений, приведенных в таблице 1, запишем формулу в следующем виде:
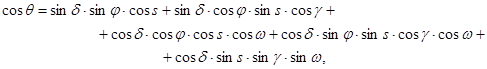 (5)
(5)
Далее находят углы, входящие в выражения (3) и (4). Значение склонения δ (рад) можно оценить по приближенной формуле Купера:
![]() (6)
(6)
где N — порядковый номер дня в году, отсчитываемый от 1 января.
Угол наклона s рассматриваемой плоскости к горизонту изменяется от 0 до π/2. Горизонтальное расположение плоскости соответствует нулю, вертикальное расположение — π/2.
Азимутальный угол плоскости γ = 0 при ориентации плоскости строго на юг, γ = π/2 при ориентации на юго-восток и γ = -π/2 при ориентации на юго-запад.
Косинус угла ω находят по формуле [3; 4]:
![]() , (7)
, (7)
Совершенно очевидно, что косинус угла падения прямого солнечного излучения Θ принимает значения от -1 до +1. Выбрав соответствующее значение величины прямого солнечного излучения из таблицы 3, рассчитанной автором, и умножив его на соответствующее значение ![]() получим значение прямого солнечного излучения, падающего на наклонную поверхность конструктивного элемента МСП, Вт/м2.
получим значение прямого солнечного излучения, падающего на наклонную поверхность конструктивного элемента МСП, Вт/м2.
Перейдем к расчету рассеянной солнечной радиации, поступающей на наклонную поверхность (без учета облачности), которая определяется по формуле [3; 4]:
D*накл= Dгор•[0,55+0,434•cos θ+0,313•(cos θ)2], (8)
где Dгор – поток рассеянной солнечной радиации (Вт/м2) на горизонтальную поверхность (s=0), определяемый по формуле Берлаге [3; 4], которую можно преобразовать к следующему виду:
![]() . (9)
. (9)
Рассчитаем значения потока рассеянной солнечной радиации на горизонтальную поверхность при различных значениях высоты солнца α и степени прозрачности атмосферы с. Результаты расчета сведем в таблицу 4.
Таблица 4
Значения рассеянной солнечной радиации Dгор при различных значениях высоты солнца α и степени прозрачности атмосферы с
|
Степень прозрачности атмосферы, с |
Высота солнца α в градусах |
||||||||||
|
7 |
10 |
15 |
20 |
25 |
30 |
40 |
50 |
60 |
75 |
90 |
|
|
Высота солнца α в радианах |
|||||||||||
|
0,12 |
0,17 |
0,26 |
0,35 |
0,44 |
0,52 |
0,7 |
0,87 |
1,05 |
1,31 |
1,57 |
|
|
0,91 |
49,19 |
66,34 |
93,21 |
115,81 |
134,91 |
149,45 |
175,39 |
193,17 |
206,51 |
217,91 |
221,54 |
|
0,67 |
47,23 |
62,81 |
86,39 |
105,47 |
121,08 |
132,66 |
152,72 |
166,02 |
175,78 |
183,97 |
186,56 |
|
0,54 |
45,56 |
59,90 |
80,99 |
97,52 |
110,72 |
120,33 |
136,60 |
147,14 |
154,76 |
161,08 |
163,05 |
|
0,43 |
43,54 |
56,46 |
74,81 |
88,71 |
99,50 |
107,19 |
119,91 |
127,96 |
133,68 |
138,37 |
139,83 |
|
0,34 |
41,17 |
52,53 |
68,07 |
79,39 |
87,92 |
93,87 |
103,48 |
109,42 |
113,58 |
116,95 |
117,99 |
|
0,27 |
38,57 |
48,36 |
61,24 |
70,24 |
76,84 |
81,35 |
88,47 |
92,78 |
95,75 |
98,13 |
98,86 |
|
0,13 |
28,98 |
34,18 |
40,15 |
43,83 |
46,31 |
47,91 |
50,30 |
51,66 |
52,57 |
53,28 |
53,50 |
Для учета уменьшения интенсивности солнечной радиации в зависимости от облачности вводится некоторый коэффициент k, который определяется как
k=1-an+0,38n2, (10)
где n — коэффициент облачности, определяемый количеством облаков в долях единицы (n = 0 при безоблачном небе, п = 1 при сплошной облачности); а — коэффициент, зависящий от географической широты местности φ, выбирается из таблицы 5. Рассчитаем возможные значения коэффициент k и результаты сведем в таблицу 5
Таблица 5
Расчетные значения коэффициента k при различных значениях коэффициента облачности и географической широты расположения МСП
|
Коэффициент облачности, n |
Географическая широта расположения МСП φ, град |
||||||||||
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
85 |
|
|
Географическая широта расположения МСП φ, рад |
|||||||||||
|
0 |
0,17 |
0,35 |
0,52 |
0,7 |
0,87 |
1,05 |
1,22 |
1,31 |
1,4 |
1,18 |
|
|
Значения коэффициента a |
|||||||||||
|
0,38 |
0,40 |
0,37 |
0,36 |
0,38 |
0,40 |
0,36 |
0,18 |
0,16 |
0,15 |
0,14 |
|
|
0 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
0,1 |
0,96 |
0,96 |
0,96 |
0,96 |
0,96 |
0,96 |
0,96 |
0,98 |
0,98 |
0,98 |
0,98 |
|
0,2 |
0,91 |
0,90 |
0,91 |
0,91 |
0,91 |
0,90 |
0,91 |
0,95 |
0,95 |
0,95 |
0,96 |
|
0,3 |
0,85 |
0,85 |
0,85 |
0,86 |
0,85 |
0,85 |
0,86 |
0,91 |
0,92 |
0,92 |
0,92 |
|
0,4 |
0,79 |
0,78 |
0,79 |
0,80 |
0,79 |
0,78 |
0,80 |
0,87 |
0,88 |
0,88 |
0,88 |
|
0,5 |
0,72 |
0,71 |
0,72 |
0,73 |
0,72 |
0,71 |
0,73 |
0,82 |
0,83 |
0,83 |
0,84 |
|
0,6 |
0,64 |
0,62 |
0,64 |
0,65 |
0,64 |
0,62 |
0,65 |
0,76 |
0,77 |
0,77 |
0,78 |
|
0,7 |
0,55 |
0,53 |
0,55 |
0,56 |
0,55 |
0,53 |
0,56 |
0,69 |
0,70 |
0,71 |
0,72 |
|
0,8 |
0,45 |
0,44 |
0,46 |
0,47 |
0,45 |
0,44 |
0,47 |
0,61 |
0,63 |
0,64 |
0,64 |
|
0,9 |
0,35 |
0,33 |
0,36 |
0,37 |
0,35 |
0,33 |
0,37 |
0,53 |
0,55 |
0,56 |
0,57 |
|
1 |
0,24 |
0,22 |
0,25 |
0,26 |
0,24 |
0,22 |
0,26 |
0,44 |
0,46 |
0,47 |
0,48 |
Таким образом, поток рассеянной солнечной радиации с учетом облачности рассчитывается по формуле
![]() (11)
(11)
Отраженное от поверхности моря и падающее на наклонную поверхность излучение, учитываемое в радиационном балансе (1), следует учитывать как поправочный коэффициент К, рассчитываемый по формуле:
![]() (12)
(12)
где К - поправочный коэффициент, А - альбедо поверхности. Альбедо различных поверхностей, возможных в условиях морского месторождения, приведены в таблицах 6 и 7. Альбедо морской поверхности зависит от высоты солнца и определяется из таблицы
Таблица 6
Зависимость величины альбедо водной поверхности от высоты солнца [4]
|
Высота солнца, α град |
5 |
20 |
45 |
50 |
90 |
|
Альбедо, А |
0,35 |
0,12 |
0,5 |
0,4 |
0,2 |
Таблица 7
Зависимость альбедо водной поверхности в зависимости от высоты солнца в зимний период
|
Поверхность |
Морской лед |
Свежий снег |
Чистый влажный снег |
Загрязненный снег |
|
Альбедо, А |
0,3-0,4 |
0,8-0,9 |
0,6-0,7 |
0,4-0,5 |
Некоторую особенность имеют вычисления рассеянной плотности теплового потока на вертикальную плоскость (s = π /2), которую находят по формуле
D*вер= Dгор•[0,55+0,434•cos θ+0,313•(cos θ)2]+0,47А(Sгор+Dгор), (13)
где Sгop — прямая солнечная радиация, поступающая на горизонтальную плоскость; А — альбедо поверхности; Dгор – поток рассеянной солнечной радиации (Вт/м2) на горизонтальную поверхность.
Учитывая, что все конструктивные элементы МСП выполнены из стальных труб, очевидным представляется оценить суммарную плотность теплового потока солнечного излучения для КЭ МСП цилиндрической формы. Совершенно очевидно, что прямому солнечному излучению при любой высоте солнца α подвергается лишь половина площади КЭ, тогда как отраженному излучению ввиду значительной площади морской акватории будет подвержена вся поверхность КЭ целиком, поэтому формула будет выглядеть следующим образом:
![]() (14)
(14)
где: Qкэ - суммарный тепловой поток солнечного излучения, R и L - внешний радиус и длина конструктивного элемента МСП в метрах.
Проиллюстрируем процессы нагрева и охлаждения на примере месторождений, расположенных на шельфе Черного моря (рис. 1). Рассмотрим стойку опорного блока, наклоненную под углом s, равным 84 градусам, и ориентированную на юг (γ=0). Совершенно очевидно, что наибольших значений плотность теплового потока солнечного излучения достигает в летний период. Так, например, для 1 июля при коэффициенте прозрачности атмосфере с, равном 0,13, максимальная плотность теплового потока Q равняется 640 Вт/м2. Процесс нагрева МСП начинается с 5:30 утра, однако значения плотности теплового потока столь невелики, что ими можно пренебречь. Начиная с 7 утра плотность теплового потока Q равняется уже 50 Вт/м2 и, возрастая по логарифмическому закону, достигает своего максимума в 640 Вт/м2 к 12 часам дня. После чего начинается равномерный процесс охлаждения, т.е. уменьшения плотности теплового потока, и к 18:00 значения плотности теплового потока становятся пренебрежимо малыми. Для тех же самых условий, но при коэффициенте прозрачности атмосферы с, равном 0,91, максимальная плотность теплового потока Q падает до 528 Вт/м2. Для 1 августа при коэффициенте прозрачности атмосферы с, равном 0,13, максимальная плотность теплового потока Q равняется 743 Вт/м2, а 31 августа эта величина Q равняется 918 Вт/м2. Отметим, что в настоящей статье рассматривается только создаваемый в результате солнечного воздействия тепловой поток без учета взаимодействия с окружающей средой, о котором будет сказано позднее.
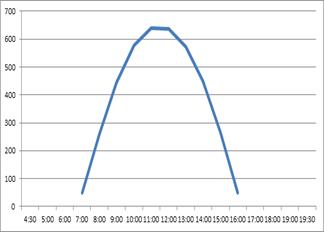
Рис. 1. Процессы нагрева и охлаждения МСП на примере месторождений Черного моря для 1 июля при коэффициенте прозрачности атмосферы с=0,13
По аналогии рассчитываются величины плотности теплового потока Q для любого морского месторождения.
Определив плотность теплового потока, можно перейти к расчету температурного режима конструктивного элемента МСП. Как известно, внутреннюю и наружную температуры стенок КЭ МСП можно выразить через плотность теплового потока, создаваемую солнечным излучением, что в свою очередь позволяет определить внешнюю температуру стенки из соотношения [2]
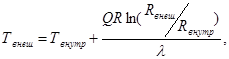 (15)
(15)
где: Q - плотность теплового потока, создаваемого солнечным излучением; ![]() - коэффициент теплопроводности [Вт/ (м• С0)]; Rвнеш, R, Rвнутр - внешний, рассматриваемый и внутренний радиусы конструктивного элемента МСП соответственно; Твнеш и Твнутр - температуры на внешней и внутренней стенках КЭ МСП. Исходя из положений, описанных в работе [2], для расчета температуры внешней стенки КЭ МСП автором предлагается использовать следующую формулу:
- коэффициент теплопроводности [Вт/ (м• С0)]; Rвнеш, R, Rвнутр - внешний, рассматриваемый и внутренний радиусы конструктивного элемента МСП соответственно; Твнеш и Твнутр - температуры на внешней и внутренней стенках КЭ МСП. Исходя из положений, описанных в работе [2], для расчета температуры внешней стенки КЭ МСП автором предлагается использовать следующую формулу:
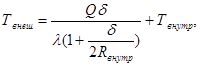 (16)
(16)
где: Q - плотность теплового потока, создаваемого солнечным излучением; ![]() - коэффициент теплопроводности; Rвнутр - внутренний радиус конструктивного элемента МСП; δ - толщина стенки конструктивного элемента МСП; Твнеш и Твнутр - температуры на внешней и внутренней стенках КЭ МСП. Данная формула, по мнению автора, в достаточной мере отражает различие между температурами внешней и наружной стенок конструктивных элементов МСП, подвергаемых воздействию со стороны солнечного излучения.
- коэффициент теплопроводности; Rвнутр - внутренний радиус конструктивного элемента МСП; δ - толщина стенки конструктивного элемента МСП; Твнеш и Твнутр - температуры на внешней и внутренней стенках КЭ МСП. Данная формула, по мнению автора, в достаточной мере отражает различие между температурами внешней и наружной стенок конструктивных элементов МСП, подвергаемых воздействию со стороны солнечного излучения.
Важной задачей является оценка динамики формирования температуры на внешней стенке КЭ МСП в зависимости от времени. Общеизвестно, что существует понятие удельной теплоёмкости — которая представляет собой физическую величину, численно равную количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу. В системе СИ удельная теплоёмкость измеряется в джоулях на килограмм на кельвин, Дж/(кг·К) и в математическом выражении представляется в виде:
![]() , (17)
, (17)
где: с - удельная теплоёмкость [Дж/(кг·К)]; ?W – количество теплоты, полученное от солнца [Дж]; m - масса конструктивного элемента МСП; ΔT — разность между рассматриваемой в данный момент времени и начальной температурами.
Отсюда следует, что
![]() . (18)
. (18)
Исходя из того что плотность теплового потока также определяется по формуле
![]() , (19)
, (19)
где: P - мощность теплового потока [Вт]; S – площадь поверхности [м2]. Мощность теплового потока определяется по формуле:
![]() , (20)
, (20)
где: ?W – количество теплоты, полученное от солнца [Дж]; ?t – продолжительность излучения [c]. Исходя из этих формул, путем простейших преобразований получим формулу
![]() (21)
(21)
откуда следует
![]() (22)
(22)
где: ![]() разность между начальной и рассматриваемой в некоторый момент времени температурами; S - площадь облучаемой поверхности [м2]; с - удельная теплоёмкость, [Дж/(кг·К)]; m - масса конструктивного элемента МСП [кг]; Q - плотность теплового потока, создаваемого солнечным излучением в некоторый рассматриваемый момент времени. Исходя из того что нами рассматриваются элементы цилиндрической формы, облучаемые с одной стороны как прямым, так и отраженным солнечным излучением, а с обратной солнечному излучению стороны только рассеянным, предполагается рассматривать эти участки отдельно. Таким образом, для участка МСП, подверженного прямому солнечному излучению, для расчета его температуры автором получена следующая новая формула:
разность между начальной и рассматриваемой в некоторый момент времени температурами; S - площадь облучаемой поверхности [м2]; с - удельная теплоёмкость, [Дж/(кг·К)]; m - масса конструктивного элемента МСП [кг]; Q - плотность теплового потока, создаваемого солнечным излучением в некоторый рассматриваемый момент времени. Исходя из того что нами рассматриваются элементы цилиндрической формы, облучаемые с одной стороны как прямым, так и отраженным солнечным излучением, а с обратной солнечному излучению стороны только рассеянным, предполагается рассматривать эти участки отдельно. Таким образом, для участка МСП, подверженного прямому солнечному излучению, для расчета его температуры автором получена следующая новая формула:
![]() , (23)
, (23)
где: Тi и Тi+1 - начальная и рассматриваемая в некоторый момент времени температура поверхности конструктивного элемента МСП, находящегося под действием прямого солнечного излучения; R - внешний радиус конструктивного элемента МСП, м; l - его длина, м; m - масса рассматриваемого участка, а остальные значения те же, что в формуле [1] и [22]. Для противоположной относительно солнечной стороны КЭ МСП при расчете ?Q исключается плотность теплового потока прямого солнечного излучения.
Проиллюстрируем приведенную методику на конкретном примере. Рассмотрим КЭ МСП площадью один квадратный метр, диаметром 530 мм с толщиной стенки 15 мм, выполненной из 09Г2С. Плотность стали в данном случае равняется 7800 [кг/м3], удельная теплоемкость 462 [Дж/кг•°С]. Коэффициент теплопроводности равен 54 Вт/ (м•°С). Рассматриваемый элемент находится с солнечной стороны.
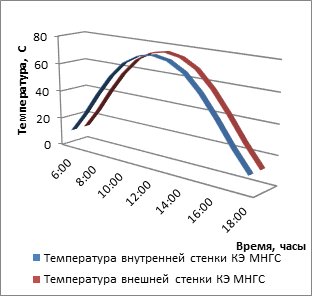
Рис. 2. Динамика изменения температуры внешней и внутренней поверхностей конструктивного элемента МСП
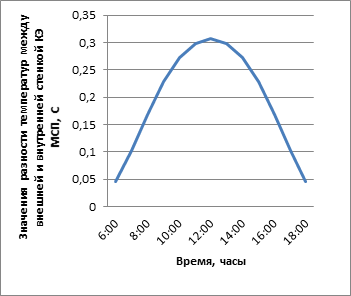
Рис. 3. Разница температур между внутренней и внешней стенками конструктивного элемента морской стационарной платформы
Таким образом, разработан новый метод оценки влияния солнечного воздействия на процессы нагрева и охлаждения МСП. Доказано, что при этом воздействии возникает разница температур между внешней и внутренней поверхностями конструктивных элементов МСП, что в свою очередь вызывает температурные напряжения, детально описанные в работе [7].
Рецензенты:
Бородавкин П.П., д.т.н., профессор, генеральный директор АО «Интергаз», г. Москва.
Литвин И.Е., д.т.н., генеральный директор ООО «СТД», г. Москва.



