Введение
Основные практические направления исследований в области механики контактного взаимодействия относятся к проблемам трения, износа, разрушения контактирующих элементов, измерения твердости, механических свойств материалов и др. В связи с этим интенсивно выявляются и изучаются закономерности деформирования в различных видах контактных задач.
Неупругое контактное взаимодействие тел является существенно менее исследованной областью механики по сравнению с упругой задачей. Достаточно развиты решения для контакта идеально-упругопластических и идеально-жесткопластических тел [1]. Для упругопластического упрочняющегося материала решение задачи связано со значительными трудностями, связанными, в частности, с отсутствием информации о форме и размерах упругопластической границы. Поэтому основные результаты в данной задаче получены численными методами [4]. При этом основное внимание уделяется зарождению пластического течения, контактным напряжениям и усилиям, распределениям напряжений в контактирующих телах, геометрическим параметрам контакта. Количественные данные о деформированном состоянии поверхности в области контакта весьма недостаточны. Это, в первую очередь, относится к геометрическим параметрам наплыва, формирующегося вокруг отпечатка. Признавая наличие наплыва, его подвергают анализу исключительно с точки зрения влияния на измеряемый диаметр отпечатка [2].
В связи с этим для описания механизма формирования наплыва вокруг отпечатка, для выявления влияния различных факторов на его параметры, для качественного и количественного описания начального напряженного состояния необходимо проведение дополнительных исследований.
Описание задачи и математическое моделирование
В настоящей работе представлены результаты моделирования задачи о вдавливании жесткого конуса в упругопластическое тело с использованием метода конечных элементов. Целью моделирования вдавливания конуса в упругопластическое тело является исследование основных геометрических характеристик перемещений и исследование влияния усилия вдавливания индентора.
Характеристики контртела:
- форма поверхности – плоская;
- материал – упругопластический, упрочняющийся;
- модуль упругости E= 2×105 МПа;
- коэффициент Пуассона m = 0,3;
- диаграмма деформирования материала – билинейная, описываемая пределом текучести sт, модулем упругости E и модулем упрочнения Eт (МПа).
Характеристики индентора:
- тип – конус;
- угол при вершине 120°;
- материал идеально упругий;
- модуль упругости E= 2×105 МПа;
- коэффициент Пуассона m = 0,3.
Входные варьируемые параметры:
- усилие вдавливания F, приложенное к индентору;
- механические свойства материала контртела в соответствии с принятой билинейной диаграммой деформирования – предел текучести sт, модуль упрочнения Eт.
Характеристики цикла нагружения модели: в начальный момент времени (t0= 0) конус контактирует с поверхностью по площадке радиусом rc® 0, нагрузка F= 0. В течение промежутка времени (t0, t1) нагрузка равномерно возрастает до значения Fmax. Затем следуют выдержка до момента времени t2 и равномерная разгрузка.
Моделирование внедрения конуса в упругопластический материал выполнено в упрощенной осесимметричной постановке [5; 7]. Расчетная схема и конечно-элементная разбивка представлены на рис. 1.
а 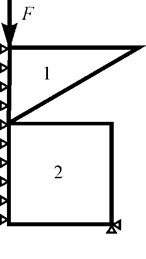 б
б 
Рис. 1. Расчетная схема (а) и конечно-элементная сетка (б)
В модели использованы элементы нескольких типов: структурные (двумерные 4-узловые) и контактные. Материал зоны 1 изотропный, упругий. В зоне 2, где происходит упругопластическое течение, материал упругопластический с билинейной диаграммой деформирования.
Важным параметром, влияющим на достоверность расчета, подробность получаемых полей напряжений и перемещений, устойчивость численного счета является размер конечного элемента. Для определения необходимой и достаточной густоты разбивки в зоне пластического течения исследовано влияние величины элемента и его формулировки на форму профиля перемещений вокруг отпечатка. Критерием необходимости и достаточности является сходимость формы профиля при измельчении разбивки. Для конструкционных сталей с билинейной диаграммой деформирования доступны две модели пластичности – с изотропным и кинематическим упрочнением. В контактной задаче возможно пластическое течение обратного знака в процессе разгрузки, поэтому использована модель пластичности с кинематическим упрочнением. Достоинством изотропной модели упрочнения является более высокая скорость счета. Для контактной задачи, в которой возможно пластическое течение обратного знака в процессе разгрузки, необходим учет Баушингера, поэтому рекомендуется использовать модель пластичности с кинематическим упрочнением [2; 4].
Проверка контактного алгоритма
С целью верификации контактного алгоритма использовано теоретическое решение задачи о сосредоточенной силе, действующей на плоскость, ограничивающую пространство [8].
На рис. 2 представлено сравнение результатов теоретического и численного решений – распределения напряжений sr(r) и sq(r) на поверхности полупространства (при z = 0) и sz(z) на оси действия силы (при r = 0). Качественное и количественное совпадение численного и теоретического решений позволили сделать заключение об адекватности используемого контактного алгоритма и применимости его для решения задачи. Адекватность самой расчетной модели проверена и подтверждена при качественном сравнении получаемых расчетных данных (распределений напряжений) с данными работ [4; 6; 9; 10].
а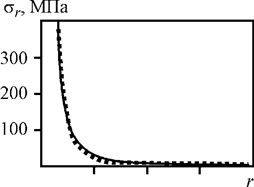 б
б 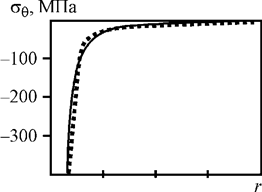 в
в 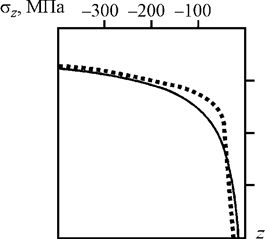
Рис. 2. Верификация контактного алгоритма: а – напряжения sr; б – напряжения sq; в – напряжения sz; сплошная линия – теоретическое решение; прерывистая линия – решение МКЭ
Программа исследования
Матрица исследования деформированного состояния поверхности вокруг отпечатка индентора для ненапряженной однородной детали представлена в табл. 1.
Таблица 1 – Матрица исследования
|
Предел |
Модуль упрочнения Eт, МПа |
|||
|
0,5·104 |
0,8·104 |
1,0·104 |
1,5·104 |
|
|
250 400 800 1000 |
● ● ● ● |
● ● ● ● |
● ● ● ● |
● ● ● ● |
Для каждой комбинации предела текучести и модуля упрочнения материала проведена серия расчетов с разными величинами усилия вдавливания индентора. Выпучивание (перемещения с положительным знаком) появляется на завершающем этапе цикла. При полном снятии нагрузки профиль перемещений включает отпечаток и область выпучивания. Перемещение поверхности упругопластического тела вокруг отпечатка и образование наплыва для предела текучести sт= 250 и модуля упрочнения Eт= 5000 Мпа представлено на рис. 3.
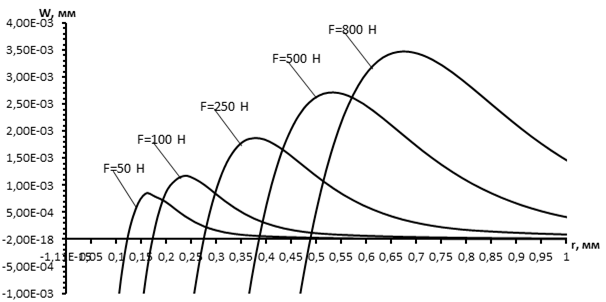
Рис. 3. Распределение нормальных перемещений в наплыве вокруг отпечатка конического индентора при различных величинах усилия вдавливания
При полном снятии нагрузки максимальное нормальное перемещение Wmax в наплыве находится на расстоянии rmax от оси z. В дальнейшем для обозначения этого характерного расстояния будем использовать термин «радиус наплыва».
Математическое описание профиля отпечатка
Для определения функции профиля отпечатка использована программа для анализа научных и статистических данных. Так как наибольший интерес в исследовании отпечатка представляет область r>rmax, в исследовании принято r>0,95rmax. Регрессионный анализ расчетных данных проведен при последовательном переборе всех возможных функций. Наилучшая сходимость и наиболее близкая к расчетным данным аппроксимация получена при использовании четырехпараметрической «Peak: Pseudo-voigt» функции
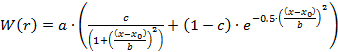 .
.
Сравнение результатов расчетов и аппроксимации для предела текучести sт= 250 и модуля упрочнения Eт= 5000 МПа представлены на рис. 4.
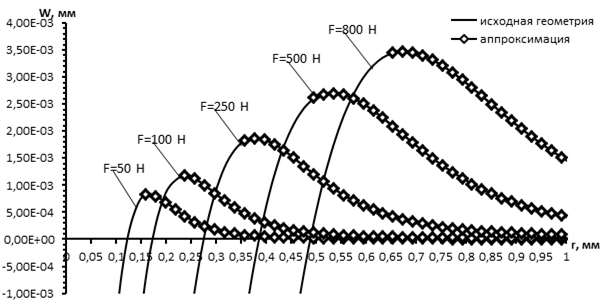
Рис. 4. Сравнение результатов расчетов и аппроксимации
Результаты аппроксимации рассмотренных наборов свойств материала и усилий вдавливания позволили установить, что параметр a при возрастании sт и Eт снижается, параметр b возрастает, параметр x0 практически не зависит от модуля упрочнения материала, а параметр с во всех исследованных вариантах близок к 1. На рис. 5 представлены графики изменения перечисленных параметров в зависимости от свойств материала тела.
а 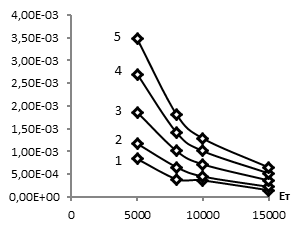 б
б 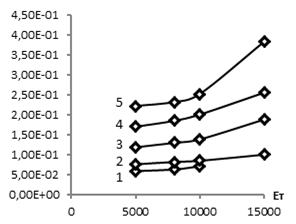
в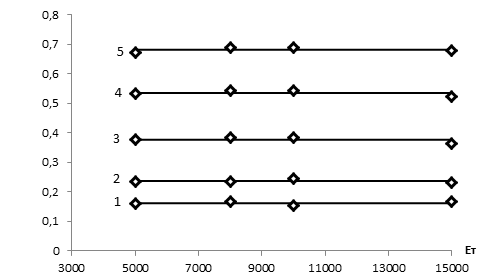
Рис. 5. Характер изменения параметров математического описания профиля наплыва в зависимости от свойств материала тела: a – параметр а; б – параметр b; в – параметр x0.
1) F=50 H, 2) F=100 H, 3) F=250 H, 4) F=500 H, 5) F=800 H
Заключение. В результате проведенных исследований разработана и верифицирована конечноэлементная модель вдавливания конического индентора в поверхность упругопластического тела. Исследована кинетика изменения распределения нормальных перемещений в наплыве вокруг отпечатка в зависимости от набора механических свойств материала тела. Установлено, что профиль наплыва при вдавливании конического индентора в поверхность упругопластического тела можно описать на участке r>0,95rmaxс помощью четырехпараметрической функции, параметры которой зависят от свойств материала. В дальнейшем это обеспечит возможность построения геометрии наплыва по данным о свойствах материала с учетом значения усилия вдавливания индентора.
Рецензенты:
Игнатьев А.Г., д.т.н., доцент, заведующий кафедрой «Сопротивление материалов», ФГБОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск.
Ерофеев В.В., д.т.н., профессор, заведующий кафедрой «Технология и организация технического сервиса», ФГБОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск.
Библиографическая ссылка
Третьяков А.А. ИССЛЕДОВАНИЕ ПРОФИЛЯ НАПЛЫВА ПРИ ВДАВЛИВАНИИ КОНИЧЕСКОГО ИНДЕНТОРА В ПЛОСКУЮ ПОВЕРХНОСТЬ УПРУГОПЛАСТИЧЕСКОГО ТЕЛА // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=10793 (дата обращения: 26.04.2025).



