Введение
Устойчивость системы характеризует способность системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Следовательно, только устойчивая система является работоспособной.
На все переходные процессы в энергосистемах действуют возмущения – начальные отклонения от номинальных параметров режима. Это могут быть отклонения значений токов, напряжений, мощностей и других параметров.
Для исследования статической устойчивости энергосистемы необходимо составить систему дифференциальных уравнений переходных процессов. Решение такой системы является сложной задачей. Для упрощения дифференциальных уравнений, описывающих энергосистему, был использован метод линеаризации «в малом» [5; 6].
В среде Matlab Simulink было смоделировано решение линеаризованной системы дифференциальных уравнений.
Для наглядности расчета коэффициентов характеристического уравнения зададимся исходным данными для схемы, представленной на рис. 1 [5].
Математическая модель энергосистемы
Для описания энергосистемы с помощью передаточных функций рассмотрим одномашинную энергосистему (рис. 1), синхронный генератор которой оборудован автоматическим регулятором возбуждения сильного действия (АРВ СД). Система дифференциальных уравнений переходных процессов для данной энергосистемы имеет вид [1]:
![]() ,
,
![]() ,
,
![]() ,
,
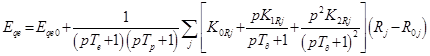 .
.
Линеаризация функции независимой переменной уравнений (1-4) приводит к производной малого приращения этой функции [5]. В результате получим линейную систему вида:
![]() .
.
Линеаризация уравнения (5) проводится относительно угла δ и синхронной ЭДС Eq.
Приращение угла δ пропорционально частоте вращения ротора генератора:
![]() ,
,
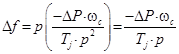 ,
,
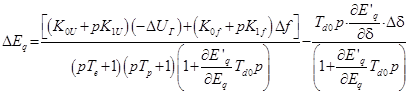 ,
,
![]() ,
,
![]() .
.
В совокупности уравнения (5-10) составляют математическую модель энергосистемы.
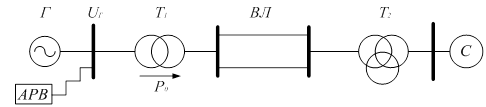
Рис. 1. Схема одномашинной энергосистемы
Для рассматриваемой одномашинной энергосистемы в качестве варьируемого параметра режима была принята активная мощность генератора. Параметрами регулирования являются модуль UГ вектора генераторного напряжения UГ и частоту f вращения ротора генератора.
Параметры схемы
Примем следующие типы электрооборудования и параметры [4]:
Генератор Г является эквивалентом двух турбогенераторов типа ТГВ-200-2УЗ. Трансформатор Т1 является эквивалентом двух трансформаторов типа ТДЦ-250000/220.
Трансформатор Т2 является эквивалентом двух групп однофазных трансформаторов типа АТДЦТН-250000/220/110.
Линия ВЛ – двухцепная, выполнена проводом марки АСО-300 с параметрами: длина ![]() ,
, ![]() .
.
Возбудитель генератора: Те=0,04 с. Регулятор возбуждения: Тр = 0,04 с.
Система С: Uc=115 кВ.
Турбина эквивалентного генератора: режим: Рт(1) = 0,5 Рmax.
Коэффициенты усиления АРВ: К0U=50 ед. возб. хх*с/ед. напряж., К1U=5 ед. возб. хх*с/ед. напряж.
Расчет коэффициентов
Для исследования установившегося режима энергосистемы запишем формулы частных производных в уравнениях:
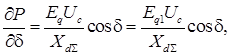
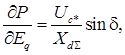
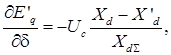
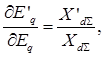
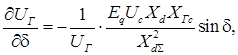
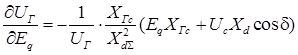 .
.
Моделирование в среде Matlab Simulink
На основе выше полученных расчетов построим одномашинную энергосистему в среде Matlab Simulink [3; 7].
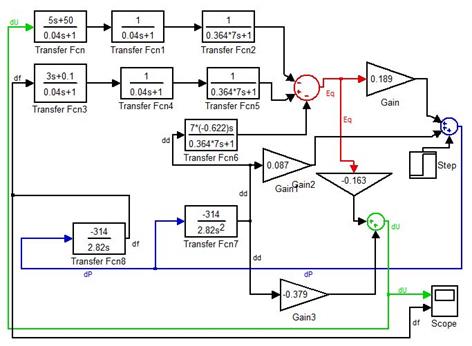
Рис. 2. Схема одномашинной энергосистемы, представленная в среде Matlab Simulink
Фиксируем коэффициенты усиления АРВ К0U и К1U по отклонению напряжения и по первой производной напряжения соответственно. Коэффициенты усиления АРВ К0f и К1f по отклонению частоты и по первой производной частоты должны попадать в область устойчивости моделируемой энергосистемы. Обычно для определения области устойчивости при проектировании энергосистем с двумя параметрами, влияющими на устойчивость энергосистемы, используют метод D-разбиений [2]. Процедура построения области устойчивости является трудоемкой. Более того, необходимо построение нескольких областей устойчивости при различных режимах работы генератора.
Используя программные средства MatLab Simulink, настройку коэффициентов усиления АРВ К0f и К1f так, чтобы система была устойчивой, можно выполнить, не прибегая к построению области устойчивости. Выполнить это можно с помощью построения корневого годографа (рис. 3).
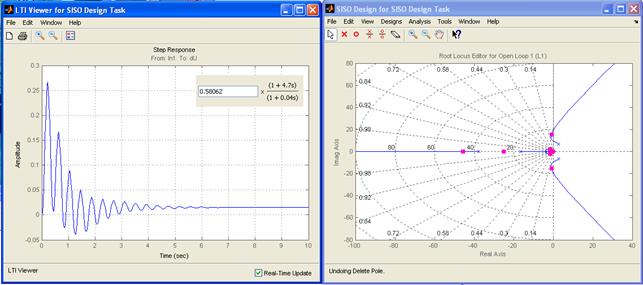
Рис. 3. Использование блока SISO Design Task при настройке коэффициентов К0f и К1f
В результате моделирования коэффициенты усиления были приняты равными К0f =0,58 и К1f =2,726. В качестве проверки нами была построена область устойчивости для данной энергосистемы методом D-разбиений. Найденные коэффициенты попадают в полученную область устойчивости.
При полученных коэффициентах усиления АРВ К0f и К1f корни характеристического уравнения располагаются в левой комплексной полуплоскости, как это видно на рис. 5. В качестве проверки сравним полюса передаточных функций с расчетами корней характеристического уравнения в MathCad при тех же коэффициентах усиления АРВ.
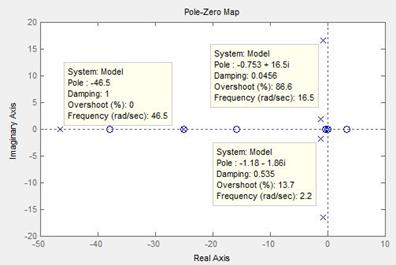

Рис. 4. График линейного анализа, показывающий корни характеристического уравнения
Из рис. 3 видно, что отклонение напряжения от заданного значения стремится к нулю, следовательно, система устойчива. Время переходного процесса в среднем составляет 10 с.
Заключение
Моделирование в среде MatLab Simulink позволяет оценить статическую устойчивость энергосистемы, определить время переходного процесса и т.д., не требуя дополнительного расчета коэффициентов характеристического уравнения и построения области устойчивости, что значительно упрощает анализ статической устойчивости энергосистемы.
Рецензенты:
Лукути Б.В., д.т.н., профессор, зав. кафедрой ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Новиков С.А., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Кулешова Е.О., Шишка Н.В. МОДЕЛИРОВАНИЕ ОДНОМАШИННОЙ ЭНЕРГОСИСТЕМЫ С ПОМОЩЬЮ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ В MATLAB SIMULINK // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=8744 (дата обращения: 07.03.2026).



