Пусть ![]() - интенсивность выпуска продукции некоторого предприятия. Предположим, что весь выпущен ный предприятием товар будет продан, а также цену товара
- интенсивность выпуска продукции некоторого предприятия. Предположим, что весь выпущен ный предприятием товар будет продан, а также цену товара ![]() будем считать убывающей функцией. Чтобы увеличить интенсивность выпуска
будем считать убывающей функцией. Чтобы увеличить интенсивность выпуска ![]() , необходимо, чтобы чистые инвестиции
, необходимо, чтобы чистые инвестиции ![]() были больше нуля. Таким образом, скорость увеличения интенсивности выпуска продукции является возрастающей функцией от
были больше нуля. Таким образом, скорость увеличения интенсивности выпуска продукции является возрастающей функцией от ![]() . Пусть эта зависимость выражается прямой пропорциональностью.
. Пусть эта зависимость выражается прямой пропорциональностью.
![]() , (1)
, (1)
где ![]() – норма акселерации. Пусть
– норма акселерации. Пусть ![]() - норма чистых инвестиций, т.е. часть дохода
- норма чистых инвестиций, т.е. часть дохода ![]() , которая тратится на чистые инвестиции, тогда
, которая тратится на чистые инвестиции, тогда ![]() .
.
Уравнение (1) запишется ![]() , где
, где ![]() .
.
Примем ![]() , где
, где ![]() . Тогда
. Тогда
![]() . (2)
. (2)
Рассмотрим ситуацию, когда два предприятия выпускают один и тот же товар. Динамика объемов, выпускаемого товара каждым предприятием, определяется следующей системой
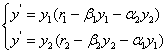 (3)
(3)
Здесь ![]() – количество, выпускаемого товара i – ым предприятием,
– количество, выпускаемого товара i – ым предприятием, ![]() - коэффициент прироста выпускаемого товара i – ым предприятием,
- коэффициент прироста выпускаемого товара i – ым предприятием, ![]() - коэффициент, описывающий влияние на интенсивность выпуска продукции в самом предприятии,
- коэффициент, описывающий влияние на интенсивность выпуска продукции в самом предприятии, ![]() - коэффициент, описывающий влияние со стороны другого предприятия. Все коэффициенты положительны. Из уравнений (3) следует, что система имеет следующие особые точки
- коэффициент, описывающий влияние со стороны другого предприятия. Все коэффициенты положительны. Из уравнений (3) следует, что система имеет следующие особые точки
1. ![]() ,
, ![]() ,
,
2. ![]() ,
, ![]() ,
,
3. ![]() ,
,![]() ,
,
4. ![]() ,
, ![]() .
.
Например для значений ![]() = 3;
= 3; ![]() = -1,8;
= -1,8; ![]() =
= ![]() =0.09;
=0.09; ![]() = –1;
= –1; ![]() = 2. Наблюдается устойчивое состояние рис. 1,2.
= 2. Наблюдается устойчивое состояние рис. 1,2.
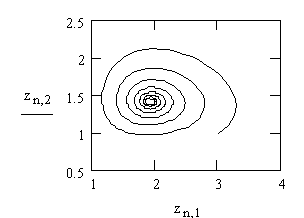
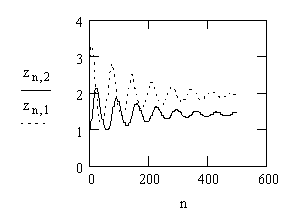
Рисунок 1,2. Расчетные данные
Для значений ![]() = 0,1;
= 0,1; ![]() = 0,5;
= 0,5; ![]() =0,05;
=0,05; ![]() =0.1;
=0.1; ![]() = 0,03;
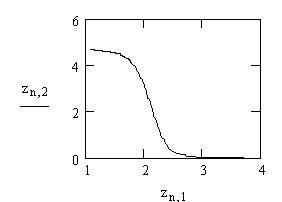
= 0,03; ![]() = 0,01 наблюдается состояние рис. 3,4.
= 0,01 наблюдается состояние рис. 3,4.
 .
. 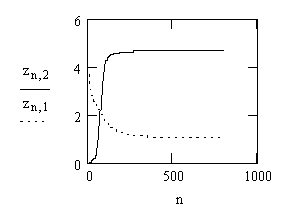
Рисунок 3,4. Расчетные данные
Исследуя систему можно сделать вывод, что при определенных условиях, если в системе в начальный момент времени существовали оба предприятия, то при любом соотношении их интенсивностей с течением времени второе предприятие полностью разорится и останется только первое со стационарным объемом ![]() зависимости от соотношения начальных объемов в системе выживает одно из предприятий. Ситуация, когда в системе сосуществуют оба предприятия с постоянными интенсивностями, является теоретически возможной, но практически крайне маловероятной.
зависимости от соотношения начальных объемов в системе выживает одно из предприятий. Ситуация, когда в системе сосуществуют оба предприятия с постоянными интенсивностями, является теоретически возможной, но практически крайне маловероятной.
При различных соотношениях пара метров, если особая точка 4 – устойчивый узел, а особые точки 2,3 – седла, то в системе устанавливается устойчивое стационарное состояние, при котором оба предприятия сосуществуют.
Библиографическая ссылка
Настин А.А., Гришин О.П., Исаев Ю.М. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ УСЛОВИЙ КОНКУРЕНЦИИ // Современные проблемы науки и образования. 2006. № 6. ;URL: https://science-education.ru/ru/article/view?id=652 (дата обращения: 06.03.2026).



