Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,039

Введение

Современное программное обеспечение электронно-вычислительной техники открывает новые методические возможности для обучения студентов в вузе с использованием компьютерной математики и информационных технологий. Системы компьютерной математики (Mathcad, Matlab, Wolfram Mathematica и т.д.) предназначены для проведения в автоматическом режиме научных, производственных и учебных задач. Богатая библиотека встроенных функций, визуально-ориентированный язык программирования и комфортный интерфейс делают отмеченные выше прикладные программы доступными для большого круга пользователей, не имеющих специальной подготовки по информатике.

Эффективное применение систем компьютерной математики при решении различных задач во многом определяется хорошей математической подготовкой пользователя, так как понимание взаимосвязей искомых величин с начальными данными решаемой задачи позволяет выбрать необходимый алгоритм вычислений и оценить адекватность полученных результатов. В рамках дисциплины «Математика» на первых курсах у будущих специалистов и бакалавров в сфере техники и технологии наземного транспорта осуществляется формирование базовой системы математических знаний, умений и компетенций, которая ориентирована на успешное освоение студентами содержания специальных математических и инженерных дисциплин на старших курсах.

Преподавание вузовского курса математики обычно проводится с позиции логического подхода [1], отражающего современную математическую картину мира. Мультимедийное оборудование лекционных аудиторий и программное обеспечение лабораторий математического моделирования позволяют включить в процесс формирования математических понятий использование вычислительных возможностей системы компьютерной математики. Применение информационных технологий в учебном процессе требует от преподавателя разработки специального методического сопровождения, которое раскрывает содержание этапов математического моделирования, составления алгоритмов решения задач и программирования вычислительных процедур.

Цель исследования – составление модели использования системы компьютерной математики в процессе формирования математических понятий у студентов, изучающих основы вузовского курса математики.

Материалы и методы исследования

Материалами представленного исследования являются научные работы по формированию математических понятий у студентов вуза в процессе применения ими систем компьютерной математики при решении учебных задач. Достижение поставленной цели осуществляется при использовании в педагогической деятельности таких научных методов, как проблемно-ориентированный анализ научных публикаций, пооперационный анализ учебной деятельности субъектов образовательного процесса, дидактическое моделирование взаимосвязи компонентов педагогических технологий.

Результаты исследования и их обсуждение

В отечественной педагогической науке процесс формирования понятий часто рассматривается с позиции теории поэтапного формирования умственных действий П.Я.Гальперина [2]. Анализируя возможности реализации цифрового подхода в обучении математическому моделированию, исследователи С.Е. Скафа, Е.Г. Евсеева и М.Е. Королев предлагают использовать ориентировочную основу учебной деятельности на практических занятиях [3]. Они обосновывают идею о том, что превращение вычислительной техники в естественный инструмент специалиста для решения современных проблем в инженерной области требует обучения его технологиям моделирования, методам нахождения оптимальных решений и анализа возможностей пакетов прикладных программ [3].

Исследователи Г.Е. Чекмарев и С.О. Фоминых отмечают значимость математической деятельности в процессе формирования понятия как мыслительного процесса, включающего математическую организацию эмпирического материала, логическую организацию математического материала и приложение математической теории для решения практических задач [4]. В своей работе по формированию математической картины мира Н.К. Туктамышов уделяет внимание вопросу о формировании математической картины мира как упорядоченной системы абстрактных объектов и отношений в процессе обучения [5]. Обобщение результатов научно-методических исследований [6, 7] и педагогической практики в условиях цифровизации [8] и информатизации [9] показывает, что преподавание системы математических знаний требует изложения теоретического материала таким образом, чтобы оно вызывало интерес у студентов и активизировало их мотивацию к обучению. Поэтому целесообразно формирование математических понятий строить по схеме, которая отражает движение от введения понятия к его применению через раскрытие содержания. В этом случае учебная деятельность студентов отображает процесс познания как переход от созерцания к осмысленному действию (таблица).

Модель формирования математического понятия

Источник: составлено авторами на основе полученных данных в ходе исследования.

Достижение дидактической цели на первом этапе (введение понятия) осуществляется через его определение и краткое ознакомление с историческими сведениями о его возникновении в науке. Построение системы знаний о математических методах познания объективной реальности (дидактическая цель второго этапа) раскрывает содержание понятия. Проведение математических преобразований и нахождение количественных значений искомых величин отражает содержание такой дидактической цели, как освоение элементов математического моделирования и алгоритмов выполнения вычислительных процедур на третьем этапе формирования математического понятия. Дополнение средств обучения системами компьютерной математики в процессе формирования математических понятий (таблица) создает благоприятные условия для развития у студентов вычислительного мышления.

Многоаспектный наукометрический анализ публикаций по проблеме вычислительного мышления проведен исследователями M. Saqr, N.G. Kwok, S.S. Oyelere, M. Tedre, а полученные ими результаты представлены в их статье [10]. Вычислительное мышление студентов, обучающихся на специальностях по информационным технологиям, член-корреспондент Российской академии образования, профессор Е.К. Хеннер определяет как набор когнитивных и некогнитивных метанавыков, создающих базу и формирующих предрасположенность к решению проблем с помощью информационных технологий [11]. Вычислительное мышление студентов, которые обучаются на специальностях и направлениях подготовки, не связанных с информационными технологиями и информатикой, можно рассматривать как понимание взаимосвязей расчетных формул в решении задачи и способность применять вычислительные средства для получения результата [12].

Широкое распространение в обучении студентов технических вузов получила система компьютерной математики Mathcad. Профессор А.А. Черняк и С.А. Богданович отмечают, что степень автоматизации вычислений должна быть такой, чтобы исключить рутинные вычисления и преобразования и раскрыть для студента идею алгоритма или суть метода с возможностью его реализации «вручную» на листе бумаги в случае упрощенной формулировки задачи [13]. Система компьютерной математики Mathcad может применяться для решения учебных задач по линейной алгебре, дифференциальному и интегральному исчислению, математической статистике [14].

Построение методики ее использования может осуществляться на основе представленной модели (рисунок).

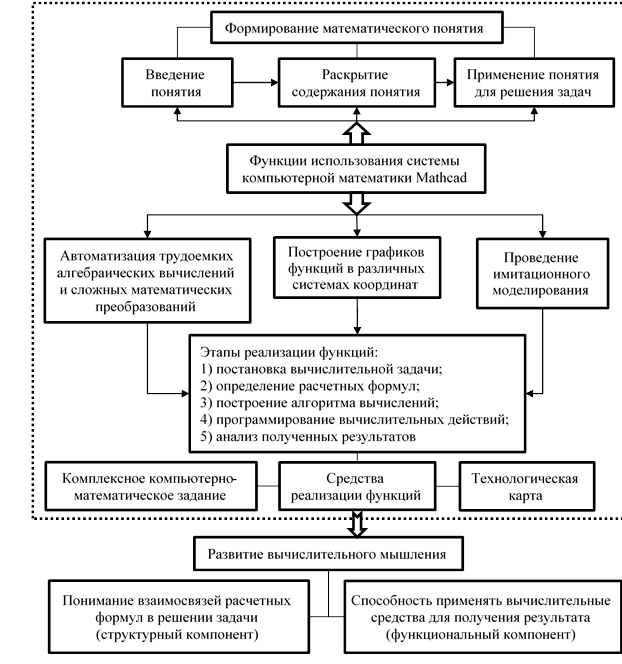
Модель использования системы Mathcad в обучении математике студентов вуза.

Источник: составлено авторами по результатам данного исследования

В случае включения системы компьютерной математики Mathcad в процесс обучения математике студентов вуза на первых двух курсах представляется целесообразным выделить представленные на рисунке три функции ее использования: автоматизация трудоемких алгебраических вычислений и сложных математических преобразований; построение графиков функций в различных системах координат; проведение имитационного моделирования [15]. Корректное применение встроенных функций из библиотеки Mathcad требует предварительного ознакомления с правилами записи значений их переменных. Визуализация графических моделей наглядно отображает тенденции изменения переменных величин. В зависимости от решаемых преподавателем дидактических целей применение системы Mathcad может осуществляться на каждом этапе формирования математических понятий в различных комбинациях ее функциональных возможностей.

Реализация отмеченных выше трех функций может распределяться на пять этапов: 1) постановка вычислительной задачи; 2) определение расчетных формул; 3) построение алгоритма вычислений; 4) программирование вычислительных действий; 5) анализ полученных результатов [16]. Вовлечение студентов в учебную деятельность по прохождению ими пяти отмеченных этапов становится возможным при составлении преподавателем комплексных компьютерно-математических заданий, выполнение которых требует применения математического моделирования и программирования вычислений [17]. Предлагаемое студентам дидактическое задание включает такие две части, как аналитико-математическая и программно-вычислительная. Первая часть содержит постановку учебной математической задачи, определение начальных условий и установление значений параметров математической модели. Вторая часть – постановку учебной задачи о построении алгоритма вычислений искомой величины и описание содержания функций пользователя в листинге программы.

Повышение эффективности решения студентами учебных задач с использованием систем компьютерной математики во многом определяется предоставлением им ориентировочной основы учебной деятельности третьего типа [2], которая оформляется в виде технологической карты и отражает последовательность совершения математических операций и их программирование. Структура технологической карты раскрывает методику формирования математических понятий, отображая содержание таких учебных действий, как конструирование математической модели и расчетных формул, построение блок-схемы алгоритма решения учебной задачи и листинга программы вычислений.

Выполнение студентами комплексных компьютерно-математических заданий с помощью технологических карт направлено не только на формирование у них системы математических знаний, умений и компетенций, но и на развитие у них вычислительного мышления. Составление математической модели решения задачи можно рассматривать как структурный компонент вычислительного мышления, а построение алгоритма вычисления искомых величин и его программирования – как функциональный компонент вычислительного мышления [12]. Если студент имеет диффузно-рассеянное представление о математическом понятии и инструментах системы компьютерной математики, то это позволяет ему выполнять учебные задания только с использованием ориентировочной основы учебной деятельности. Осознанное использование встроенных функций системы компьютерной математики для нахождения количественных значений искомой величины становится возможным, если в сознании студента сформирована система математических знаний, умений и навыков.

Понимание студентами технологии применения систем компьютерной математики в процессе решения учебных задач создает благоприятные условия для развития у них познавательного интереса к исследовательской деятельности. Осознанное включение студентами инженерных специальностей и направлений подготовки современных информационных технологий в свою учебную деятельность позволяет им успешнее осваивать различные вычислительные методы, которые необходимы для решения профессионально-ориентированных задач при изучении специальных дисциплин на старших курсах в вузе. Умения студентов применять системы компьютерной математики при выполнении трудоемких инженерных расчетов во многом облегчают им написание курсовых проектов и дипломной работы.

Заключение

Возможным вариантом активизации учебной и познавательной деятельности студентов вуза в процессе их обучения математике может выступать применение предлагаемой модели использования системы компьютерной математики Mathcad. Важно не забывать о том, что обращение с мощными вычислительными инструментами требует от пользователя хорошей подготовки как в области математики, так и информатики. Включение современных информационных и вычислительных технологий в процесс формирования математических понятий позволяет преподавателю разрабатывать новые дидактические задания и методическое сопровождение, что положительно влияет на развитие его профессионально-личностного потенциала.