Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Широко применяемые в пищевой, фармацевтической и электронной промышленности, а также на складах, дельта-роботы открывают новые возможности для обучения школьников робототехнике. Данная статья посвящена исследованию потенциала интеграции дельта-роботов с компьютерным зрением в учебный процесс. Дельта-роботы, благодаря своей параллельной кинематической структуре, обеспечивают высокую скорость и точность при выполнении широкого спектра задач, от монтажа микроэлектронных компонентов до упаковки готовой продукции [1].

Дельта-робот – это манипулятор, придуманный Рэймондом Клавэлем, он получил такое название благодаря своей конструкции, напоминающей греческую букву Δ. Он состоит из трех рычагов, соединенных с основанием и несущих на себе исполнительный орган [2].

Основные достоинства дельта-роботов:

‒ Прочность конструкции: нагрузка распределяется между несколькими звеньями, что уменьшает нагрузку на каждое звено в отдельности и повышает общую жесткость системы [3].

‒ Высокая скорость работы сервоприводов: благодаря использованию нескольких легких параллельных звеньев, дельта-роботы имеют небольшую массу и поэтому способны достигать очень высоких скоростей перемещения [4].

‒ Высокая точность позиционирования исполнительного механизма: жесткие параллельные связи в дельта-роботах позволяют достичь высокой повторяемости и стабильности позиционирования даже при высоких скоростях [2].

Оснащенные системами компьютерного зрения, эти роботы способны распознавать объекты различной формы и размера, что позволяет им адаптироваться к меняющимся условиям производства.

Проект по созданию дельта-робота с компьютерным зрением является логическим продолжением предыдущих исследований авторов в области школьной робототехники [5, 6]. Опираясь на успешный опыт руководства школьными проектами по разработке роботов-манипуляторов, авторы предложили школьникам амбициозную задачу, связанную с созданием высокоскоростного и точного дельта-робота с компьютерным зрением. Сложность проекта заключается в необходимости решения ряда инженерных задач, включая разработку механической конструкции, углубленного изучения кинематики и создание алгоритмов управления и компьютерного зрения. Благодаря практическому опыту школьников в области робототехники и программирования, поставленные задачи были решены в полном объеме.

Цель исследования – проектирование и описание методики реализации школьниками образовательного проекта «Дельта-робот с компьютерным зрением», направленного на постепенное освоение обучающимися сложных инженерных задач и развитие у них навыков самостоятельного решения проблем.

Материалы и методы исследования

Методика работы над проектом состояла из нескольких этапов: определение задач проекта, выполнение работы, обсуждение результатов.

Перечень основных компонентов: детали конструкторов LEGO® Mindstorms EV3 и Pitsco TETRIX® Max, контроллер и 4 сервопривода LEGO® Mindstorms EV3, USB веб-камера A4 Tech 2.0, прошивка leJOS для LEGO® Mindstorms EV3, среда MIT App Inventor.

Цель и задачи первого этапа (выполнены в 7 классе):

Сконструировать и запрограммировать дельта-робота для сортировки кубиков на конвейерной линии с помощью датчика цвета(рис. 1).

1) сборка каркаса, кинематических цепей с сервоприводами;

2) разработка программы на родной среде LEGO® Mindstorms EV3 автоматической сортировки кубиков, поступающих по конвейерной ленте, по цвету;

3) программирование системы управления манипулятором на языке Java.

Рис. 1.Дельта-робот для сортировки кубиков по цветам на конвейерной линии

Цель и задачи второго этапа (выполнены в 9 классе):

Сконструировать и запрограммировать дельта-робота для сортировки разбросанных кубиков по цветам с помощью видеокамеры (рис. 2), решить следующие задачи:

1) сборка каркаса, кинематических цепей с сервоприводами и установка видеокамеры;

2) разработка алгоритмов компьютерного зрения на языке Java для распознавания цветных кубиков с помощью видеокамеры и библиотеки OpenCV;

3) расчет углов сервоприводов позиционирования исполнительного механизма (захвата);

4) интеграция алгоритмов управления манипулятором и компьютерного зрения;

5) разработка приложения для смартфона, который будет управлять манипулятором, на Scratch в MIT App Inventor. Приложение должно иметь функцию записи перемещений манипулятора для многократного автоматического повторения.

Рис. 2.Дельта-робот для сортировки разбросанных цветных кубиков

Проектирование дельта-робота с видеозрением

После многочисленных экспериментов с имеющимися в школах наборами, включая использование металлических деталей и платформы Arduino, наилучших результатов удалось достичь с третьим вариантом конструкции дельта-робота, основанным на наборе LEGO® Mindstorms EV3. Использование сервоприводов EV3 позволило обеспечить высокую точность позиционирования звеньев, а жесткость и точность изготовления пластиковых элементов минимизировала прогибы и люфты в механизмах. В результате точность позиционирования исполнительного органа намного повысилась, а повторяемость движений улучшилась.  Благодаря достаточной вычислительной мощности и широкой распространенности в образовательных учреждениях, LEGO® Mindstorms EV3 стал идеальным выбором для реализации проекта «Дельта-робот с видеозрением».  Разнообразие поддерживаемых языков программирования делает EV3 универсальным инструментом для обучения и исследований.

Для реализации системы компьютерного зрения использовалась USB веб-камера, подключенная к контроллеру EV3, работающая под управлением альтернативной прошивки leJOS 0.9.1-beta. Камеру (черное устройство с проводом на рис. 2) установили на верхнюю платформу дельта-робота таким образом, чтобы вся рабочая зона была в поле ее зрения.

Алгоритмы обработки изображений были разработаны на языке Java с использованием открытой библиотеки компьютерного зрения OpenCV 2.4.11, предоставляющей необходимый и достаточный набор инструментов для обработки изображений в рамках намеченного проекта. Для распознавания цвета были использованы цветовые пространства HSV и методы пороговой обработки (рис. 3).

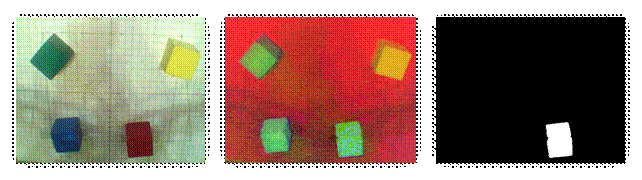
Рис. 3.Преобразование изображения в HSV и получение маски

OpenCV анализирует черно-белую маску, где белые области соответствуют обнаруженному цвету. OpenCV находит контуры на двоичной маске, используя функцию findContours. Полученные контуры представляют собой упорядоченные последовательности точек, описывающих границы объектов (рис. 4). Эти контуры записываются в специальный массив List<MatOfPoint>. Из всех найденных контуров выбирается самый большой, так как он, скорее всего, соответствует цели поиска (красному кубику). Вокруг этого контура рисуется минимальный ограничивающий прямоугольник, центр которого принимается за центр объекта (красного кубика). Контроллер EV3 обрабатывает изображение и вычисляет местонахождение кубика за 6 с.

Рис. 4.Определение положения кубика в координатной системе манипулятора

Для того чтобы определить углы трех сервоприводов, необходимых для позиционирования захвата манипулятора над обнаруженным кубиком, необходимо решить обратную задачу кинематики для сконструированного манипулятора.  В интернете можно найти сложные математические модели для расчета движений дельта-роботов, основанные на стереометрии и тригонометрии [4, 7]. Однако авторы предлагают более простой и понятный школьникам подход – табличный метод. Школьники смогут заполнять таблицу значений углов сервоприводов для разных положений манипулятора. Это позволит им сосредоточиться на механической сборке и программировании, не углубляясь в сложные математические вычисления.

Поскольку ограниченная допустимыми углами манипулятора рабочая зона находится в горизонтальной плоскости, а кубики имеют довольно крупный размер, авторы предположили, что манипулятор может захватить кубики из 48 положений внутри рабочей зоны (рис. 4). Для упрощения вычислений ограничили рабочую зону прямоугольником.

Чтобы перевести координаты центра кубика из пикселей в удобную для робота систему координат, делим их на определенное число (в данном случае на 20). Это позволяет сопоставить положение объекта на изображении с положением исполнительного механизма манипулятора робота. В результате получаем координаты {5;4} в системе координат робота, которые указывают на то место, где находится красный кубик (рис. 4). Осталось определить углы трех сервоприводов для всех 48 точек рабочей зоны.

Чтобы уменьшить количество работы, решено вручную определить углы сервоприводов только для 9 точек вместо 48, а остальные для быстроты рассчитать по линейной зависимости. Однако после наблюдения за движениями манипулятора, который в центре ощутимо опускал исполнительный механизм вниз, пришли к мнению, что формула круга будет более близка к истинной зависимости, а некоторая неточность нивелируется люфтом несовершенного манипулятора.

Для этого вручную выставляем манипулятор в трех положениях в каждом из трех рядов, отмеченных красными крестиками на бумаге в рабочей зоне (рис. 5), и записываем углы трех моторов плеч. Видно, что рабочая зона выглядит с камеры трапецией, поскольку камера установлена сбоку. Для ускорения процесса получения углов оставшихся координат написана программа на Java для расчетов оставшихся пяти положений углов трех сервоприводов плеч на основе данных о трех положениях захвата манипулятора.

Рис. 5. Размеченная в клетку рабочая зона дает 48 положений манипулятора

Для получения недостающих пяти точек из восьми применяем формулу окружности. Сначала находим центр окружности и радиус по трем точкам, на основании чего находим уравнение окружности, проходящей по известным трем точкам (рис. 6).

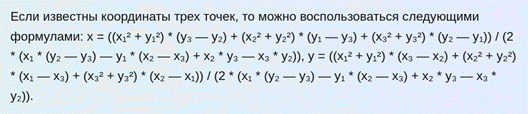
Рис. 6. Нахождение формулы круга по трем точкам

Далее, подставляя координату х в полученное уравнение, находим все 48 необходимых углов для каждого сервопривода (рис. 7).

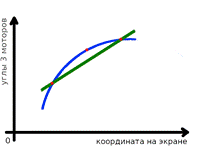
Рис. 7. Сравнение отклонения линейной и круговой зависимости угла от координаты

Для хранения найденных положений исполнительного механизма манипулятора решено использовать словарь из 48 элементов. В программе на Java словарь выглядит примерно как Map<Point, Angles[ ]>, где ключ – это координата, а значение – массив с тремя углами сервоприводов, соответствующий этой координате.

Расчет движений манипулятора на основании созданного алгоритма с описанным словарем позволил полноценно управлять дельта-роботом. При необходимости имеется возможность несколько раз повысить точность позиционирования манипулятора.

Также на языке Scratch в MIT App Inventor разработан дистанционный пульт на смартфоне Android, который расширяет возможности дельта-робота.

Функциональные возможности разработанного школьниками дельта-робота:

1) автоматическая сортировка роботом предметов с помощью видеокамеры (робот автоматически определяет местонахождение цветных кубиков и перетаскивает их в соответствующие цвету кубика контейнеры);

2) дистанционное управление манипулятором через Bluetooth с пульта, реализованного на смартфоне Android;

3) функция ручного программирования перемещений исполнительного механизма с дистанционного пульта (робот может в ускоренном темпе повторять перемещения, совершенные человеком, например, для автономной работы в производстве).

Результаты исследования и их обсуждение

Описанный и реализованный проект дельта-робота уникален благодаря характеристикам, качественно не уступающим промышленным образцам, и доступным компонентам для его изготовления.

Дельта-роботы с компьютерным зрением обладают высокой степенью гибкости и адаптивности, что делает их идеальными для образовательных целей. Для расчета траекторий можно применять как традиционные методы (стереометрия, планиметрия), так и современные подходы, основанные на машинном обучении [7]. Декартов манипулятор по своей природе не требует сложных математических расчетов и больше подходит для начального обучения. В то время как обратная задача кинематики многозвенного шарнирного манипулятора с компьютерным зрением уже сложновата для школьников [5].

Молниеносные и точные движения звеньев дельта-робота, не похожие на человеческие, завораживают детей и создают дополнительный интерес к его изучению.

Заключение

Разработанный дельта-робот стал результатом успешного школьного проекта, демонстрируя, что даже в юном возрасте можно создавать сложные технические системы. Проект не только позволил школьникам углубить знания в области электроники, программирования и механики, но и развить навыки системного мышления и решения инженерных задач. Увлечение конструированием роботов стало для школьников трамплином к новым достижениям: они демонстрируют хорошие результаты на олимпиадах по точным предметам.

Дельта-робот с системой компьютерного зрения является гибким и эффективным инструментом образовательной робототехники для развития у школьников комплексных навыков: от электроники и конструирования до алгоритмического мышления. На базе таких роботов можно создавать более простые или сложные системы, адаптированные под широкий спектр учебных задач, от автоматизации лабораторных экспериментов до моделирования производственных процессов.