Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

В судебно-медицинской науке вопросам исследований, связанных с установлением времени смерти человека, отводится особое место [1], что обусловлено важностью этих исследований для органов следствия и судопроизводства [2]. Причем следует отметить, что наибольший интерес вызывают разработки, применяющиеся специалистами в области судебной медицины непосредственно в ходе осмотра трупа на месте его обнаружения, поскольку многие признаки, используемые для диагностики давности смерти, теряют свою диагностическую значимость при перемещении трупа в другие условия (относительно первоначального места происшествия) или по мере увеличения продолжительности времени, прошедшего с момента смерти до начала изучения мертвого тела [3].

Термометрия как способ исследования мертвого тела уже более 150 лет используется судебными медиками всего мира. Разработано большое количество способов измерения температуры трупа, для чего предложены оригинальные диагностические зоны и создан математический аппарат в форме уравнений, описывающий наблюдаемый процесс, – феноменологические математические модели [4]. Указанные модели разработаны их авторами на основе различных математических законов (линейного, параболического, S-образного и др.), что позволяло авторам решать вопрос установления давности смерти с различной степенью точности [5, с. 11–84; 6]. Авторы настоящей статьи неоднократно, так же как и некоторые другие исследователи, указывали, что в судебно-медицинских целях следует использовать только класс экспоненциальных моделей как наиболее точных в диагностическом плане. Причем наивысшие показатели точности достигаются только в том случае, если моделирование постмортальной температуры осуществлялось комплексным учетом взаимосвязи поверхностной и глубокой температур трупа, в свою очередь, обусловленных значением внешней температуры – подкласс двухэкспоненциальных моделей [7]. В современной судебной медицине из данного подкласса моделей наиболее часто используют выражения, разработанные C. Hennsge [8] и T.K. Marshall, F. Hoare E. [9]. Несмотря на значительный возраст этих моделей, они характеризуются высокой точностью описания постмортальной температуры и в актуальных модификациях позволяют учесть некоторые индивидуальные особенности конкретного мертвого тела и условий его нахождения – колебания температуры окружающей среды [10], ее отрицательную величину [11], срыв «температурного гомеостаза» и умирание человека с температурой, отличающейся от «прижизненной нормы» [12], и т.д.

Однако, несмотря на возможности указанных моделей, они не применялись ранее для описания температур мертвого тела, находящегося в условиях инсоляции, и, соответственно, отсутствуют научно обоснованные рекомендации по применению математического моделирования в случаях термометрического исследования трупа, на который воздействовала прямая солнечная радиация [13].

Цель исследования

Создание способа математического моделирования посмертной температуры трупа, находившегося в условиях инсоляции, на базе конечно-разностной (послойной) математической модели, для применения его в целях определения давности смерти человека по тепловому способу.

Материал и методы исследования

Методологической составляющей проведенного научного исследования явилось первоначальное осмысление изучаемого явления, т.е. изменения температуры трупа в условиях инсоляции, теплофизических процессов, происходящих в мертвом теле в указанных внешних условиях, построение адекватной математической модели описываемого процесса.

Методом познания в ходе исследования стал эксперимент, средством – экспериментальное оборудование (заменяющие труп объекты (манекены), имеющие геометрию человеческого тела). Технологией проведения эксперимента являлась регистрация теплофизических процессов, происходящих в трупе при действии на него прямой солнечной радиации.

На начальном этапе выполнения исследования проведен анализ (метод-операция) научной литературы (исторический метод операционного эмпирического исследования), позволивший определить степень разработанности проблемы. В результате проведенного анализа были сформулированы цели и задачи научной работы, выстроены рабочие гипотезы (с использованием познавательных действий теоретических методов), установлены объекты исследования и подобраны методы их изучения.

Экспериментальная часть работы выполнена как на замещающих труп объектах (ЗТО), так и на реальных телах – объектах судебно-медицинской экспертизы.

Естественно, что перед началом исследования оно прошло рассмотрение на заседании комитета по медицинской и биологической этике ФГБОУ ВО ИГМА Минздрава России, с получением необходимого одобрения (положительное заключение от 21.10.2021 г. № 09-21).

ЗТО представляли собой мешки из прочного полиэтилена, плотно заполненные умеренно влажным черноземом без посторонних включений. Суммарно на ЗТО было выполнено 46 экспериментов общей продолжительностью 984 часа. За это время было выполнено 1810 термоизмерений.

Справедливость научных положений, сформулированных на основе экспериментов на ЗТО, проверена на реальных мертвых телах (9 трупов) с заведомо известной причиной и временем смерти. Все тела относились к взрослым лицам обоего пола, различного возраста, не имели грубых повреждений диагностической зоны (печени), используемой в исследовании.

В сериях экспериментов моделировались условия воздействия на тело прямых солнечных лучей. При этом тело лежало на открытой местности при ясной безветренной погоде. Моделирование одежды трупа осуществлялось путем оборачивания объекта в один слой х/б ткани различных расцветок.

Термометрия ЗТО осуществлялась путем введения иглы электротермометра в центральную часть объекта. Термометрия трупов производилась в печени по методике П.И. Новикова и Е.Ф. Шведа [14, с. 107–108]. Регистрация температуры окружающей среды осуществлялась путем размещения датчика электротермометра рядом с объектом таким образом, чтобы исключить его прямой нагрев солнечными лучами либо непосредственным контактом с объектом и предметами окружающей обстановки.

Результаты исследования и их обсуждение

Для правильной оценки механизмов влияния прямой солнечной радиации на процесс изменения температуры трупа исключительно важным является понимание того факта, что излучение солнца, главным образом инфракрасная часть его спектра, нагревает не воздух, а поверхности и предметы, находящиеся в зоне прямых солнечных лучей. Соответственно, представив процесс передачи тепла из глубоких отделов трупа (1-й узел модели) к его поверхности и во внешнюю среду физическим аналогом, в качестве которого произвольно избрав систему сообщающихся сосудов с жидкостью, получим возможность учесть приращение температуры на поверхности трупа (10-й узел модели). В физическом аналоге это соответствует поступлению дополнительного объема жидкости в 10-й (последний) узел физического аналога (рис. 1).

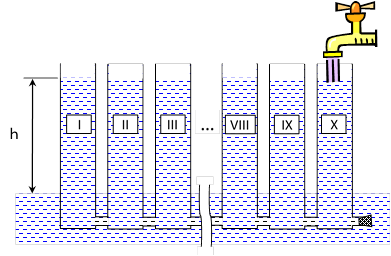
Рис. 1. Физический аналог тепловых процессов в трупе при воздействии на его поверхность прямой солнечной радиации (инсоляции)

В математическом отображении этот процесс может быть представлен в дискретном виде системой уравнений, отражающих изменение температур в узлах модели в интервале времени небольшой продолжительности. При этом величина и направление изменения температуры каждого из узлов определяются суммарным градиентом температур в данном узле и в двух соседних с ним, а также общей продолжительностью времени моделирования.

Приращение температуры в последнем – внешнем – узле может быть учтено путем введения новой, ранее не использованной, переменной – S, которой было решено присвоить собственное обозначение – «солнечный фактор».

Таким образом, в упрощенной форме процесс охлаждения трупа, находящегося под воздействием прямых солнечных лучей на его поверхность, может быть представлен в виде следующей конечно-разностной математической модели (системы уравнений) [15]:

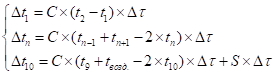(1)

где t1-t10 – расчетные значения температур в узлах модели на момент начала интервала времени ∆τ;

∆t1-∆t10 – изменение температур в узлах модели за период времени ∆τ (повышение температуры принимается за положительное изменение, снижение температуры – за отрицательное изменение);

n – номера узлов (с 2-го по 9-й);

под индексами (1...10, n) обозначены номера узлов модели;

tвозд. – температура воздуха;

Δτ – продолжительность одного шага моделирования (0,01 часа);

C – коэффициент, отражающий теплообменные параметры трупа;

S – солнечный фактор.

В ходе проведения экспериментов на ЗТО установлено, что наиболее значимое влияние на величину «солнечного фактора» с точки зрения точности описания моделируемых температурных процессов оказывают масса самого объекта, время года как фактор, определяющий сезонную динамику интенсивности инсоляции, и цвет текстильной ткани (одежды), покрывающей объект.

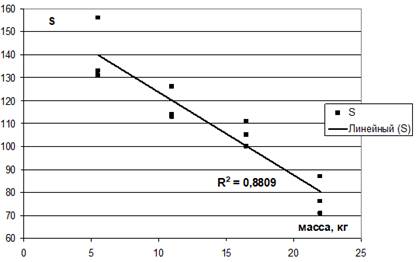
Рис. 2. Зависимость величины фактора S от массы объекта

Зависимость между массой объекта (m) и значением параметра S графически представлена на рисунке 2.

Установлено, что зависимость между массой объекта и величиной S может быть описана уравнением линейной регрессии:

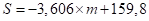(2)

где S – солнечный фактор;

m – масса объекта, кг.

Однако необходимо отметить, что указанная зависимость установлена в сериях экспериментов на ЗТО, но не подтверждена обнаружением какой-либо зависимости при исследовании реальных мертвых тел. По мнению авторов, это объясняется тем обстоятельством, что для проверки положений, полученных на ЗТО, использованы трупы исключительно взрослых лиц, и их анатомо-морфологические (ростовесовые) характеристики различались несущественно.

Это позволило сделать вывод, что, по крайней мере для трупов взрослых людей, можно рекомендовать к практическому применению средние значения «солнечного фактора» независимо от массы конкретного мертвого тела. Так, например, для летнего периода и для трупов людей, обернутых в хлопчатобумажную ткань черного цвета, такое среднее значение оказалось равным 100,5, а для трупов, обернутых в х/б ткань белого цвета, – 60,7.

Влияние времени года на значение «солнечного фактора» (S) изучалось на ЗТО массой 22 кг, покрытом черной хлопчатобумажной тканью. Исследования производились в зимний, летний и осенний периоды. При этом авторы считают возможным не производить исследования в весенний период, поскольку основным фактором, определяющим сезонную динамику интенсивности инсоляции, служит угол высоты солнцестояния, а этот показатель для весеннего и осеннего периодов является идентичным.

Установлены статистически достоверные различия между значениями «солнечного фактора» (S) для летнего, осеннего (весеннего) и зимнего периодов года. Оценки средних величин S для каждого из сезонов составили:

– для летнего периода 78,0;

– для осеннего (весеннего) периода 58,67;

– для зимнего периода 37,67.

Полученные данные позволили рассчитать понижающие коэффициенты значений «солнечного фактора» для весенне-осеннего и зимнего периодов года по отношению к максимальным значениям, устанавливаемым для летнего сезона. С некоторым округлением для практического применения могут быть предложены следующие значения сезонных коэффициентов (KS):

– для осеннего периода 75%, (≈ 58,67 / 78,0);

– для зимнего периода 50%, (≈ 37,67 / 78,0).

Методом однофакторного дисперсионного анализа произведена статистическая обработка значений «солнечного фактора» (S), полученных при изучении результатов исследований, произведенных на ЗТО одной массы (22 кг) в летний период года, но обернутых в текстильную ткань разных цветов (черного, красного, желтого, зеленого, синего, белого). При этом выявлено наличие высокой значимости цвета ткани использованных образцов текстиля в формировании значения этого параметра. Полученные оценки средних значений S для каждого из цветов варьировали в пределах между 34 – для белой текстильной ткани и 78 – для черной ткани. При этом субъективно более темные цвета образцов ткани соответствовали более высоким значениям S.

Наличие статистически значимых различий «солнечного фактора» для одежды различного цвета ткани подтверждено и в экспериментах на трупах. Как пример ниже представлен график (рис. 3), демонстрирующий различие значений S для трупов, покрытых тканью черного и белого цветов.

Для объективной оценки влияния световоспринимающих свойств образцов текстиля на значение «солнечного фактора» (S) в конкретном практическом случае специально разработана методика, основанная на использовании офисного сканера. Методика состоит из двух этапов. На первом этапе производятся сканирование образца текстиля и сохранение изображения образца текстиля в файле графического формата Bitmap (*.bmp). На втором этапе сохраненное в файле изображение анализируется специально разработанной компьютерной программой, производящей количественную оценку яркости образцов, выраженную в процентах, для которой введено обозначение «W». Абсолютно черному цвету соответствует значение W, равное 0, абсолютно белому цвету – значение, равное 100%.

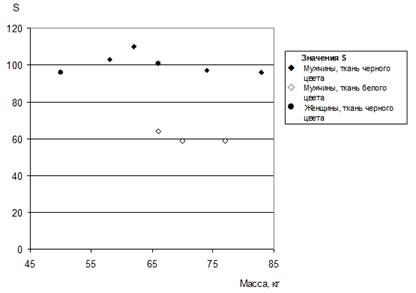
Рис. 3. Зависимость величины фактора S от массы объекта и цвета ткани

Установлено наличие статистически значимой (коэффициент корреляции 0,924) линейной зависимости между параметром S и уровнем яркости образца текстиля (W), что математически может быть выражено в виде уравнения линейной регрессии:

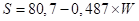(3)

где S – солнечный фактор;

W – яркость поверхности, в % по отношению к белому.

Методика проверена и в исследованиях на трупах в летний период с использованием двух образцов текстильной ткани – черного и белого цветов. Полученные средние значения «солнечного фактора» для этих цветов текстиля (соответственно 100,5 и 60,7) позволяют рассчитать коэффициенты линейной регрессии зависимости «солнечного фактора» (S) от уровня яркости (W) для трупа (в летний период года):

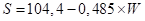(4)

где S – солнечный фактор;

W – яркость поверхности, в % по отношению к белому.

Именно это выражение (с использованием сезонных понижающих коэффициентов) можно рекомендовать для применения при определении значений параметра S для практического моделирования температурных процессов в целях диагностики давности смерти.

Необходимо также принимать во внимание, что для определения абсолютных значений констант, отражающих интенсивность воздействия инсоляции на труп, существенное значение имеют географическое положение (географическая широта) и условия микроклимата, прежде всего, прозрачность атмосферы на месте проведения исследований.

Настоящее исследование проводилось в условиях промышленного города – Челябинска. Его географические координаты 55°10′ северной широты и 61°24′ восточной долготы. Есть все основания для правомерности использования без сколько-нибудь существенной корректировки результатов настоящего исследования в местностях, относящихся в средней полосе России. К этой зоне можно отнести такие города, как Москва, Казань, Уфа, Екатеринбург, Ижевск, Курган, Новосибирск, Кемерово, Красноярск и др. Для других территорий, значительно отличающихся по географическому положению от Челябинска в южную или северную сторону, по-видимому, необходимо использование дополнительного поправочного зонального коэффициента (KZ), уточнение которого потребует определенных исследований в конкретных местностях.

С учетом всего вышеизложенного окончательная формула для расчета так называемого солнечного фактора (S), отражающего интенсивность воздействия солнечной радиации на труп, может быть представлена в следующем виде:

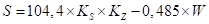(5)

где S – солнечный фактор;

KS – сезонный коэффициент;

KZ – зональный коэффициент;

W – яркость поверхности, в % по отношению к белому.

Статистическая обработка результатов математического моделирования процесса охлаждения трупа в условиях воздействия на его поверхность солнечного излучения и термоизмерений, полученных на экспериментальном материале, позволяет оценить возможную ошибку определения давности смерти, накапливаемую за 6,4–8,5 часа наблюдений, – /±0,42 часа (±25 минут) при p=0,05, что в процентном отношении составляет 5,6% от продолжительности инсоляции.

Выводы

1. Результатом работы явилось создание на основе описанных ранее математических моделей нового математического аппарата, позволяющего корректно учитывать при моделировании посмертного изменения температуры трупа воздействие на этот процесс прямой солнечной радиации.

Соответствие разработанной математической модели реальным температурным кривым проверено путем глубокой термометрии в исследованиях на замещающих труп объектах (ЗТО) и на трупах людей при воздействии на них прямой солнечной радиации.

2. По результатам исследований на ЗТО и на трупах установлены факторы, определяющие значение параметра, отражающего интенсивность влияния солнечной радиации на посмертную динамику температуры трупа, – «солнечный фактор» (S). Значение «солнечного фактора» определяется исходя из величины световоспринимающей способности поверхности объекта и календарного времени года, от которого зависит угол падения солнечных лучей на объект.

3. Разработанный математический аппарат и выявленные закономерности пригодны для использования в целях установления давности наступления смерти в случаях, когда труп до обнаружения находился в условиях инсоляции, что подтверждается высокой точностью созданного метода. Оценка составляющей погрешности моделирования температуры, обусловленной учетом влияния солнечной радиации, по результатам настоящего исследования при p=0,05 составила 25 минут за период инсоляции (6,4–8,5 часа), что не превышало 5,6% от продолжительности инсоляции.