Важным аспектом развития современных образовательных технологий является использование в обучении различным дисциплинам, в том числе и математическим, цифровых образовательных сред [1, 2, 3]. Электронный курс «Дифференциальные уравнения» в цифровой образовательной среде NOMOTEX (ЦОС NOMOTEX) разработан на кафедре «Вычислительная математика и математическая физика» МГТУ имени Н.Э.Баумана. В течение последних пяти лет он прошел апробацию и корректировку при обучении будущих инженеров и математиков. ЦОС NOMOTEX содержит в себе теоретические материалы изучаемых дисциплин, семинары с подробным описанием приемов, правил, алгоритмов, применяемых при решении задач, большое количество разобранных примеров по всем темам курса, наборы оценочных средств [4].
Цель исследования: на примере курса «Дифференциальные уравнения» показать структуру домашних заданий, выполняемых студентами в ЦОС NOMOTEX, а также особенности автоматической проверки решений дифференциальных уравнений и их графической интерпретации в данной среде.
Материал и методы исследования
Обязательным контрольным мероприятием курса «Дифференциальные уравнения» является домашнее задание, которое выдается на определенный срок и появляется в личном кабинете каждого студента. При разработке домашних заданий разработчики столкнулись с трудностью автоматизированной проверки ответов, связанной с их неоднозначностью (различными способами представления функций) и необходимостью графической интерпретации. В статье описаны алгоритмы проверки ответов для задач различного типа.
Структура домашнего задания
Домашнее задание содержит в себе алгоритм решения задач и индивидуальное условие для каждого студента (рис. 1).
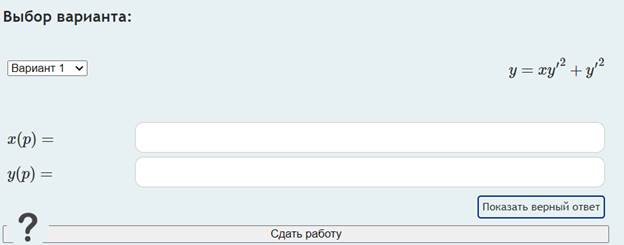
Рис. 1. Структура домашнего задания
Вариант каждого студента индивидуален, он выдается так называемым случайным образом. Количество возможных условий каждого задания системой никак не ограничено, что позволяет составить большой банк задач и исключить повторы.
Студент самостоятельно вносит ответ к задаче, и система показывает, верен он или нет. Количество попыток внесения ответа не ограничено. Это позволяет студенту сразу понять, что в задаче допущена ошибка, и исправить ее. Возможность самопроверки существенно сокращает количество работы преподавателя.
Система оценивает правильность итогового ответа, но не может проверить каждый шаг выполненного задания. По этой причине студент должен сам разобраться, где он допустил ошибку, что развивает навыки самостоятельной работы. В том случае, если ошибку не удается исправить самостоятельно, студент обращается к преподавателю за консультацией. Отметим, что обязательным элементом решенной задачи является не только ввод верного ответа, но и оформленное в тетради решение, сканированную копию которого студенты прикрепляют к домашнему заданию.
Алгоритм проверки ответов
Одним из самых сложных этапов разработки цифровой образовательной среды является алгоритм проверки ответов к задачам [5, 6, 7].
Проверка введенных ответов в ЦОС NOMOTEX полностью автоматизирована. Система позволяет обработать введенный ответ в течение нескольких секунд, иногда время немного увеличивается в зависимости от вида полученной функции.
Известно, что при решении дифференциальных уравнений может быть получен неоднозначный ответ. Одну и ту же функцию можно представить в разном виде. Поэтому основным способом проверки служат последовательное дифференцирование функции и подстановка ее и полученных производных в начальное уравнение для получения верного тождества. Причем алгоритм работает не только для явно заданных функций, ответ может быть введен и в виде не явно заданной функции. К каждой задаче есть инструкция для ввода ответа (рис. 2).
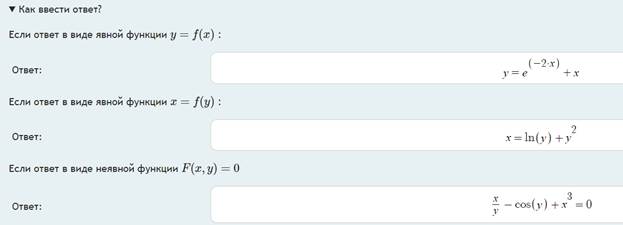
Рис. 2. Инструкция для ввода ответов
Встречаются задачи, в которых описанный выше алгоритм проверки не работает. В частности, это уравнения, не разрешенные относительно производной. Примером такого задания является уравнение Лагранжа, где ответ представляется в виде системы функций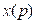 
, 
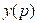, зависящих от параметра 
.
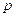Пример
Решить уравнение
.
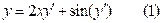Решением уравнения является система функций:
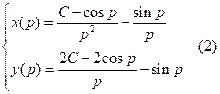
Проверка проходит в несколько этапов.
Сначала в исходном уравнении (1) выполняется замена переменной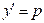 
, получаем
.
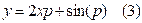На первом этапе проверки в уравнение (3) подставляется решение (2) для получения верного тождества.
На втором этапе дифференцируем уравнение (3) по переменной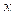 
:
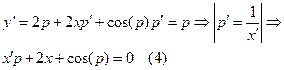
В уравнение (4) подставляем 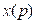для получения верного тождества.
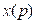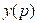Если в решении есть ошибка, то двухэтапная проверка позволяет понять, при вычислении какой из двух функций системы, или , допущена ошибка.
Визуализация решения
Одним из разделов курса «Дифференциальные уравнения» является теория устойчивости. При решении задач этого раздела требуется не только дать однозначный итоговый ответ, но и проинтерпретировать его графически.
ЦОС NOMOTEX позволяет визуализировать полученное решение.
Задания этого раздела требуют нестандартных подходов к алгоритму проверки. Приведем пример такой задачи:
Построить фазовые траектории системы дифференциальных уравнений.
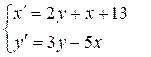
Задача состоит из нескольких вопросов, ответы на которые нужно внести студенту:
1. Единственность положения равновесия.
2. Корни характеристического уравнения.
3. Координаты точки покоя.
4. Тип точки покоя.
5. Уравнения главных изоклин.
6. Тип фазовых траекторий.
7. Направление движения.
8. График.
За каждый пункт баллы начисляются отдельно, что позволяет начислять баллы за частично выполненную задачу. Все пункты подразумевают единственно верный однозначный ответ.
Решение данной системы задает фазовые траектории – множество кривых, заданных параметрически.
.
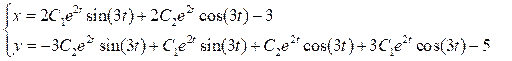В процессе разработки курса возник вопрос, как осуществить проверку верности построенного фазового портрета. Каждая траектория имеет достаточно громоздкое уравнение в параметрической системе координат, причем одной траекторией построение не ограничивается. Вводить каждое уравнение не представляется возможным, так как на это уходит очень много времени, поэтому был разработан алгоритм, по которому студент выбирает верный график из набора готовых. Создана база со всеми возможными графиками для данного задания, каждый из которых является верным для одного из всех имеющихся вариантов. Траектории разделены на группы, каждой из которых присвоен свой номер.
В данной задаче было использовано четыре основных типа фазовых траекторий. Если студент изначально указывает неверный тип, ему выпадают заведомо ошибочные графики, которые могут быть верными для другой задачи. Графики, из которых предстоит выбрать верный, очень похожи между собой (рис. 3).
Рис. 3. Варианты ответов в задании на построение фазовых портретов
Построение фазового портрета зависит от выбранной точки покоя. Начало координат автоматически меняется при вводе центра новой системы координат. Также в данной задаче необходимо выбрать верное направление движения (от точки покоя или к точке покоя), что тоже возможно осуществить в данной системе. Направление меняется автоматически, при изменении выбора, так же как и все графики.
Заключение
В данной работе показаны способы решения проблем, возникающих при поиске алгоритмов автоматической проверки ответов к задачам по курсу «Дифференциальные уравнения».
Возможность автоматической проверки ответов позволяет студенту самостоятельно проверить правильность выполненного задания и вовремя исправить неверные решения, развивает у студентов навыки самостоятельной работы при поиске ошибок в выполненных заданиях, упрощает работу преподавателя по проверке домашних работ. Все это в совокупности способствует улучшению результатов обучения.
Библиографическая ссылка
Димитриенко Ю.И., Анисова Т.Л., Смехнова А.А., Алесин А.В. АВТОМАТИЗАЦИЯ ПРОВЕРКИ ДОМАШНЕГО ЗАДАНИЯ В КУРСЕ «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ» В ЦИФРОВОЙ ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ NOMOTEX // Современные проблемы науки и образования. – 2023. – № 6. ;URL: https://science-education.ru/ru/article/view?id=33163 (дата обращения: 28.04.2024).