Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В последние десятилетия в связи со стремительным развитием социальных процессов и необходимостью научного управления развитием общества задача создания точных и надежных прогнозов становится все более актуальной. Ускорение информатизации общества, непрерывная динамика условий жизни и производства, неопределенность процессов социального, экономического и политического характера обусловливают потребность в специалистах, способных прогнозировать результаты своего труда на основе научного стохастического обоснования с учетом существующих рисков. Это требование справедливо и для специалистов среднего звена, что вызывает необходимость дальнейшего совершенствования математической подготовки среднего профессионального образования.

Целью исследования является уточнение с позиций профессионально-деятельностного подхода к обучению содержания и структуры понятия «прогностическая компетентность специалиста среднего звена» как результата формирования прогностической деятельности в процессе математической подготовки в колледже технического или экономического профиля.

Материал и методы исследования. В работе проводится анализ нормативных документов, определяющих требования к результатам подготовки специалистов в концепции среднего профессионального образования, и научно-педагогической литературы по теме исследования, изучен и обобщен педагогический опыт реализации математической подготовки в колледже.

Результаты исследования и их обсуждение. В основу Федерального государственного образовательного стандарта среднего профессионального образования нового поколения (ФГОС СПО) заложен компетентностно-деятельный подход. При этом требования и результаты подготовки специалистов представлены в виде общих, общепрофессиональных и профессиональных компетенций.

ФГОС СПО большинства технических и экономических направлений подготовки содержат компетенции, подразумевающие овладение прогностической деятельностью. Профессиональные стандарты этих специальностей также содержат умения, связанные с прогностической деятельностью. Примеры компетенций ФГОС СПО и Профстандартов, соответствующих прогностической деятельности, представлены в таблице 1.

Таблица 1

Примеры компетенций ФГОС СПО и Профстандартов специалистов среднего звена, соответствующих прогностической деятельности

На основе анализа ФГОС СПО и Профессиональных стандартов специалистов среднего звена технических и экономических профилей нами выделены следующие общие умения, входящие в состав прогностической деятельности.

1. Прогнозировать структуру выполнения профессиональных задач.

2. Оценивать и анализировать итоги выполнения задач профессиональной направленности.

3. Решать расчетные задачи с использованием информационных технологий.

4. Составлять план профессиональной деятельности, обеспечивать составление расчетов на производстве.

5. Оценивать потенциальные риски и возможности при планировании изменений в производстве.

6. Прогнозировать требования в модификации объемов ресурсов, необходимых для обеспечения работы.

Таким образом, прогностическая деятельность является неотъемлемой составляющей профессиональной деятельности выпускников технических и экономических колледжей.

Поскольку прогностическая деятельность подразумевает использование количественных методов математики, то ее формирование, в основном, осуществляется в рамках математической подготовки.

Результатом математической подготовки будущего специалиста большинство исследователей считают его математическую компетентность [1,с.3]. Поэтому мы рассматриваем прогностическую компетентность как составляющую математической компетентности, которая, в свою очередь, входит в состав профессиональной компетентности выпускника колледжа (рисунок).

Содержание и структура математической подготовки в колледже разрабатываются на основе примерной образовательной программы к ФГОС СПО с учетом их уровня и направленности.

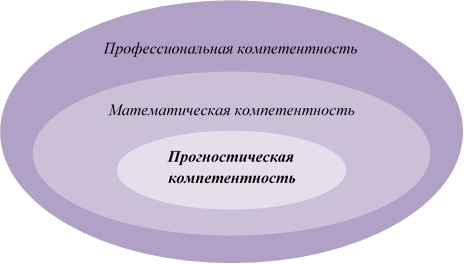Взаимосвязь компетентностей специалиста среднего звена

Согласно учебным планам некоторых специальностей СПО 2023/2024 учебного года, на математические дисциплины в колледже отводится количество часов, представленное в таблице 2.

Таблица 2

Математическая подготовка в системе СПО

По данным таблицы 3 можно сделать вывод о том, что объем математической подготовки в СПО достаточен для формирования математической компетентности специалиста как основного результата математической подготовки, а следовательно, и прогностической компетентности специалиста среднего звена. Тем не менее, учитывая межпредметный характер современного образования, заметим, что математическая компетентность специалиста формируется в рамках не только базовых математических дисциплин (математика, алгебра и геометрия и др.), но и прикладных и профильных дисциплин (теория вероятности и математическая статистика, основы бухгалтерского учета, организация расчетов с бюджетом и внебюджетными фондами и др.).

В научно-педагогических исследованиях существуют разные трактовки понятий «прогностическая деятельность», «прогностическая компетентность».

Н.А. Сайфуллина определяет прогностическую компетентность как навык будущего специалиста мобилизовать в своей профессиональной сфере знания и умения по прогнозированию, а также способы разработки прогнозов [2, с. 72].

А.И. Нижников определяет прогностическую компетентность как неотъемлемую часть профессиональной компетентности, поскольку прогностическая компетентность специалиста предоставляет возможность составлять прогнозы как в повседневной, так и в его профессиональной деятельности, а также в ходе анализа некоторых моделей, проектов и в процессе профессионального роста [3, с. 64].

О.М. Растопчина выделяет прогностическую компетенцию студентов естественно-научного профиля как часть профессиональной культуры, которая проявляется в способности и готовности реализовать математические знания, умения, навыки и способы прогнозирования, планирования, проектирования, обоснования научного эксперимента, производственной деятельности и профессионально-личностной траектории саморазвития [4,с. 143].

Общим для большинства исследователей является понимание прогностической компетентности как неотъемлемой составляющей профессиональной и математической компетентностей специалиста.

В нормативных документах, регламентирующих подготовку специалистов среднего звена, формулировка компетенций, по мнению авторов, представлена в общем виде, допускает неопределенную интерпретацию содержания и не позволяет однозначно определить и оценить результаты их сформированности. Например, из формулировок «ОК-9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности» и «ПК-2.7. Выполнять контрольные процедуры и их документирование, готовить и оформлять
завершающие материалы по результатам внутреннего контроля» не ясно, о какой «смене технологий» идет речь, что необходимо проделать специалисту в процедуре «внутреннего контроля», как будут осуществляться «контрольные процедуры», каким будет результат данных действий.

Для решения проблемы целеполагания при реализации математической подготовки в колледже предлагаем использовать профессионально-деятельностный подход к построению модели специалиста как цели обучения [5, с. 6]. В основу профессионально-деятельностного подхода положена идея известного российского психолога Н.Ф. Талызиной, которая заключается в следующем: разрабатывая цели обучения по определенному предмету, в первую очередь, следует выделить основную систему задач, которую обучающийся будет готовиться решать [6,с.102]. Таким образом, если разработать систему типовых профессиональных задач специалиста среднего звена, связанных с прогностической деятельностью, и методы решения таких задач в обобщенном виде, то это позволит уточнить цели и содержание обучения в колледжах технического и экономического профилей [7,с.8].

По результатам анализа взглядов на определение прогностической деятельности, на основании требований к ней ФГОС СПО, выделение особенностей и содержательных элементов удалось уточнить понятие прогностической деятельности и прогностической компетентности будущих специалистов технического колледжа с позиций профессионально-деятельностного подхода.

Под прогностической деятельностью специалиста среднего звена в настоящем исследовании будем понимать вид его профессиональной деятельности по реализации обобщенных методов решения профессиональных задач прогнозирования, требующих использования математических знаний.

Прогностическая компетентность специалиста среднего звена – это результат овладения прогностической деятельностью как способность решать математическими методами типовые прогностические задачи специалиста среднего звена.

Типовая прогностическая задача (ТПЗ) специалиста среднего звена – цель, которую он регулярно ставит в процессе своей профессиональной деятельности по прогнозированию ее результатов.

Анализ нормативных документов, содержания профильных дисциплин в системе подготовки специалистов среднего звена, а также знакомство с экспертными мнениями специалистов в технической и экономической сферах позволили выделить ТПЗ, при решении которых специалисту требуется использование математических методов прогнозирования. Типы прогностических задач специалиста среднего звена, конечные продукты их решения и примеры ТПЗ представлены в таблице 3.

Таблица 3

Типология прогностических задач специалиста среднего звена

А.В. Лапшова, М.И. Колдина, Н.В. Пескова под прогностическими умениями понимают владение совокупностью умственных и практических действий, нацеленных на решение прогностических задач на базе сознательного применения на практике психолого-педагогических и методологических знаний. Структура прогностических умений включает: сбор диагностической информации; постановку целей; выдвижение гипотез, перспектив развития личности и коллектива; предвидение последствий и вариантов деятельности; проверку правильности постановки задач и моделирования; коррекцию модели; проектирование индивидуальной программы личностного развития студента; составление прогноза [8, с. 45].

Обратимся к структуре деятельности по А.Н. Леонтьеву: деятельность включает интеллектуальный, волевой и эмоциональный компоненты, специальное общенаучное исследование перспектив развития каких-либо процессов [9, с. 57].

Допустимо, на первый взгляд, что все элементы прогностической деятельности имеют разнообразные названия, но в то же время их терминологическое содержание имеет практически единую содержательную структуру. Таким образом, с точки зрения всех авторов, элементами прогностической деятельности считаются владение способами, средствами и методами прогнозирования; деятельности, не мыслимые без прогнозирования, такие как планирование, моделирование, проектирование; субъективные качества (мотивация, рефлексия, самоорганизация и планирование личностной траектории развития и профессионального роста).

Данные, описанные в научно-педагогической литературе, и эмпирический опыт предоставили возможность определить структуру прогностической деятельности специалиста среднего звена с точки зрения выделенного авторами направления реализации (табл. 4).

Таблица 4

Структура прогностической деятельности специалиста среднего звена

Каждому элементу структуры прогностической деятельности, по нашему мнению, соответствует собственный состав общекультурных и профессиональных компетенций, формирование которых средствами учебных дисциплин математической подготовки предусмотрено ФГОС СПО специальностей 18.02.09 Переработка нефти и газа, 09.02.06 Сетевое и системное администрирование, 38.02.01 Экономика и бухгалтерский учет (по отраслям), 42.02.01 Реклама. Набор соответствующих образовательных компетенций приведен в таблице 5.

Таблица 5

Соответствие компетенций структуре прогностической деятельности

Установленное в таблице 5 соответствие позволяет обосновать возможность совместной реализации профессионально-деятельностного и компетентностного подходов к формированию прогностической деятельности специалистов среднего звена.

Для каждого типа прогностических задач специалиста среднего звена был выделен обобщенный метод решения (действия обобщенных методов составляют инструментальный компонент прогностической деятельности). Поэтому формирование инструментального компонента прогностической деятельности при изучении математических дисциплин осуществляется через формирование обобщенных методов решения ТПЗ. Пример решения ТПЗ первого типа в соответствии с действиями обобщенного метода приведен в таблице 6.

Задача. Определите плановую себестоимость продукции (С). Затраты на выпуск продукции предприятием в отчетном году составили 4000 тыс. р., при этом условно-постоянные расходы (СПОСТ) равны 2200 тыс. р. В плановом периоде предусматривается увеличение выпуска продукции на 20%.

Таблица 6

Обобщенный метод решения ТПЗ первого типа

Целесообразно преподавателю со студентами вместе выделить обобщенный метод решения ТПЗ, зафиксировать и использовать его в качестве ориентировочной основы при решении любых прогностических задач данного типа. При многократном самостоятельном применении методов решения ТПЗ прогностическая деятельность становится стилем мышления студентов.

Заключение. Представленный опыт формирования прогностической деятельности при обучении математике в Астраханском государственном техническом университете на факультете среднего профессионального образования технических и экономических специальностей показал, что студенты стали увереннее справляться с решением профессиональных прогностических задач, в том числе при освоении профильных дисциплин и подготовке выпускных квалификационных работ.