Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В математике понятие множества считается одним из основных.Под множеством понимают собрание объектов какого-либо рода, например множество книг, множество игрушек, множество домов, множество чисел. Объекты, составляющие множество, называются элементами множества.

Теория множеств является основным разделом математики. А само понятие множества относится к фундаментальным и первичным понятиям в математике. Понятия теории множеств применяют при формулировке многих понятий математики школьного курса. Язык теории множеств используется при обучении учащихся школьному курсу математики, но не применяется в обосновании школьного курса математики.

При решении различных задач из курса математики 5–6-х классов у учащихся возникают проблемы, связанные с недостатком знаний о множествах и операций над множествами.

Понятиями «множество чисел» и «множество геометрических фигур» пользовались до того, как возникла теория множеств. При этом геометрические фигуры трактовались как целостные объекты, а не как состоящие из точек. Для задания геометрической фигуры в математике применялись конечные наборы точек. Например, для того, чтобы задать отрезок, достаточно было задать две точки – границы отрезка, не обращая внимания на множество точек между ними. Теория множеств и теоретико-множественный подход к определению математических понятий позволили геометрические фигуры определять как множества некоторых объектов.

Анализ учебников [1–3] по математике за 5-й класс позволил выявить, что в 5-м классе школьники не изучают тему «Множества». Начинается изучение этой темы только в 6-м классе, хотя на интуитивном уровне этим понятием пользуются и в начальной школе. Такой перерыв в овладении учащимися теоретико-множественными понятиями является неоправданным, отрицательно сказывается на качестве знаний школьников.

При изучении темы «Умножение и деление десятичных дробей» в 5-м классе по программе «Математика-5» Н.Я. Виленкина и иных [4] учащиеся должны научиться приводить примеры конечных и бесконечных множеств. При изучении темы «Делимость чисел» в 6-м классе по программе «Математика-6» Н.Я. Виленкина и иных [5] учащиеся знакомятся с понятиями объединения и пересечения множеств, учатся изображать эти понятия с помощью диаграмм Эйлера–Венна.

При изучении курса математики 6-го класса по программе «Математика-6» С.М. Никольского и иных [6] учащиеся знакомятся с понятиями числовых множеств: множества целых чисел, множества рациональных чисел, осваивают понятия конечных и бесконечных числовых множеств.

В учебнике «Математика-6» Г.В. Дорофеева и иных [7] имеется глава «Множества. Комбинаторика», в которой выделены следующие разделы: 1) Понятие множества; 2) Операции над множествами; 3) Решение задач с помощью кругов Эйлера; 4) Комбинаторные задачи.

В результате изучения данной главы шестиклассники должны научиться: 1) приводить примеры конечных и бесконечных множеств натуральных и множеств целых чисел; 2) владеть операциями объединения и пересечения конкретных множеств; 3) изображать множества с помощью кругов Эйлера–Венна; 4) выявлять соотношения между числовыми множествами; 5) приводить примеры несложных классификаций из различных областей жизни; 6) решать комбинаторные задачи методом перебора вариантов.

Г.В. Дорофеев в учебнике «Математика-6» рассматривает понятия множества, конечного бесконечного множества, пустого множества, подмножества, две операции над множествами (объединения и пересечения).

На многие понятия теории множеств, которыми школьники пользуются при изучении новых тем, не обращается должного внимания. Например, перед изучением тем «Сравнение натуральных чисел», «Сложение и вычитание натуральных чисел» в 5-м классе целесообразно познакомить учащихся с понятиями «множество», «числовое множество», «множество натуральных чисел».

Эффективному усвоению учащимися 5–6-х классов элементов теории множеств, на наш взгляд, способствует система заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь. С каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает.

Цель исследования: показать, что использование системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, способствует эффективному усвоению учащимися элементов теории множеств и повышению уровня практических умений при выполнении заданий по данной теме.

Материалы и методы исследования. Для достижения поставленных целей были проведены анализ и критическое осмысление методико-математической литературы по проблеме исследования, а также состояния исследуемой проблемы в практике работы школы. Далее проведен эксперимент с целью выявления влияния системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, на повышение уровня практических умений учащихся по теме «Теория множеств».

Результаты исследования и их обсуждение. В качестве примера рассмотрим систему заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, по двум темам теории множеств. Перед заданиями дается краткая теория по данной теме. В школьных учебниках для 5–6-х классов Г.В. Дорофеева, Н.Я. Виленкина задания по теме «Теория множеств» расположены бессистемно и не содержат дозированной помощи.

Тема 1. Множества. Элементы множества

Изучаем теорию: Множествами называют различные совокупности объектов. Объектами могут быть натуральные числа, квадраты, буквы русского алфавита и другие объекты. Множества на письме обозначают заглавными буквами латинского алфавита: A, Х, C, ..., У.

Множество, которое не содержит ни одного объекта, называется пустым множеством и обозначается символом ∅. Объекты, из которых состоит множество, называются элементами множества. Элементы множества обозначают строчными буквами латинского алфавита: a, х, c, у. Для обозначения принадлежности элемента х множеству Х применяют знак ∈ – «х ∈ Х». Если элементх не принадлежит множеству Х, тоиспользуют запись: «х 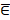Х», или « х ∉ Х». Обозначения числовых множеств: N – множество натуральных чисел,N0 – множество целых неотрицательных чисел, Z – множество целых отрицательных чисел, Q – множество рациональных чисел.

Выполняем следующие задания:

Задание 1. Назовите три элемента множества:

- Дней недели;

- Нечетных натуральных чисел;

- Целых чисел, делящихся на пять;

- Четырехугольников.

Продолжи перечислять элементы множеств:

- Понедельник, вторник,________________;

-3, 5, ________________

- 10, 15, ________________

- Квадрат, трапеция, _______________

Задание 2. Запишите, используя символы:

- Число 7 – целое;

- число – 4 не является целым неотрицательным числом;

- Число 0 – целое;

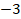- – число отрицательное.

Продолжи выполнять по образцу.

- 7 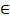Z;

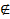- -4 N0;

- __________;

- __________.

Задание 3. Укажите, верными или неверными являются высказывания:

a) – 3 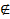N с) 5,36 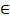Q e) 0 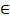Z

b) 10 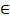Z d) 0,5 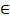N f) 100 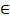N

Решение:

a) ________________, b) ________________, c) _________________

c) _______________, d) ________________, f) _________________

Задание 4. L – множество целых чисел, больших 9 и меньших 16. Запишите с помощью знаков ∈ и ∉ , какие из чисел 7, 8, 6, 12, 15, 16 ему принадлежат, а какие не принадлежат.

Решение

________________________________

________________________________

Задание 5. Даны числа 1; 0; – 12; –16; 125; 3. Определите, какие из них являются:

a) натуральными;

b) целыми;

c) целыми неотрицательными.

Решение :

a) __________________; b)_____________________; c)__________________________.

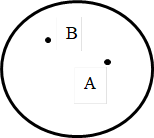
Задание 6. С – множество точек окружности, изображенной на рисунке 1:

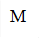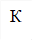Рис.1

Укажите верные высказывания: а) А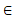С, b)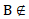С, c) М ∈ С, d) К ∉ С.

Решение:

a) _____________;

b) _____________;

c) _____________;

d) _____________;

Тема 2. Способы задания множеств

Изучаем теорию: Говорят, что множество является заданным, если о каждом объекте этого множества можно сказать, принадлежит он данному множеству или не принадлежит.

Множество можно задать путем перечисления всех его элементов или указания характеристического свойства его элементов. Характеристическое свойство множества – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

Выполняем следующие задания:

Задание 1.

Запишите, используя знака равенства и фигурные скобки, следующие предложения:

a) К – множество однозначных чисел;

b) М – множество букв a, b, c, d;

c) L – множество, состоящее из треугольника, круга и ромба.

Продолжи выполнять по образцу:

a) К =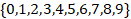

b) ___________________

c) ___________________

Задание 2.

Запишите с помощью символов множество Д, если оно состоит из целых чисел:

a) больших 80, но меньших 100;

b) меньших 1200;

c) больших –5, но меньших 3.

Продолжи выполнять по образцу:

a) М =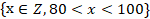

b) _______________________

c) _______________________

Задание 3.

Перечислите элементы следующих множеств:

А – множество четных двузначных чисел;

В – множество нечетных двузначных чисел;

С – множество натуральных чисел, меньших или равных 12;

Д – множество двузначных чисел, делящихся на 5.

Решение:

a) _________________________________;

b) _________________________________;

c) _________________________________;

d) _________________________________;

Задание 4.

Укажите характеристическое свойство элементов множества:

1. {а, е, ё, и, о, у, э, ю, я, ы};

2. {46, 69, 92, 115, 138};

3. {111, 222, 333, 444, 555, 666, 777, 888, 999}

Продолжи выполнять по образцу:

1. Множество гласных букв русского алфавита;

2. ­­­­­­­­­­­­­­­­­­­______________________________________;

3. ______________________________________;

Задание 5.

К – множество трехзначных чисел, в записи которых встречается цифра 2. Принадлежат ли этому множеству числа 23; 322; 261; –112?

Ответ запишите, используя знак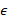и и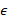

Продолжите выполнять по образцу:

23 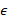К, ____________________________

Задание 6.

Множество С состоит из числа 26, отрезка и трапеции. Принадлежат ли этому множеству диагональ трапеции, середина отрезка и число 13 – делитель числа 26?

Решение:

_________________________________________________.

В эксперименте по выявлению уровня влияния использования системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, на повышение уровня практических умений учащихся 5–6-х классов принимали участие школьники двух групп в течение 2020/2021 учебного года. В контрольной группе (120 человек) обучение элементам теории множеств проводилось без применения системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, а в экспериментальной группе (130 человек) – с использованием разработанной системы заданий. Учащимися контрольной группы выполнялись те же самые задания, что и учащимися экспериментальной группы, только без дозированной помощи. Для оценки эффективности использования системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, были выделены уровни распределения учащихся. Уровни выявлялись по следующим показателям: умение выполнять задания на использование языка теории множеств и умение выполнять задания навыполнениеопераций над множествами. Критериями распределения детей по уровням выступали отметки: «5» – высокий уровень (2 показателя в полном объеме), «4» – средний уровень (2 показателя, но нев полном объеме, с небольшими замечаниями), «3–2» низкий уровень (2 или 1 показатель с серьезными ошибками, отсутствие показателей).

Полученные результаты на начало эксперимента приведем в таблице 1.

Таблица 1

Результаты на начало эксперимента

Приведем результаты, полученные на конец эксперимента в таблице 2.

Таблица 2

Результаты на конец эксперимента

Согласно таблицам можно заключить, что уровень практических умений школьников экспериментальной группы повышается по сравнению с уровнем участников контрольной группы.

Заключение. Использование разработанной нами системы заданий, расположенных по принципу «от простого к сложному», содержащих дозированную помощь, в которой с каждым последующим заданием мера помощи уменьшается, а доля самостоятельности ученика возрастает, способствует эффективному усвоению элементов теории множеств и повышению уровня практических умений учащихся, что подтвердил проведенный нами эксперимент.