Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ланкин М.В. 1 Наракидзе Н.Д. 1 Ланкин А.М. 1

---

1 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образо-вания «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова»

В статье описан метод получения топографии магнитного поля в окрестностях образца из магнитомягкого материала с помощью множественного регрессионного анализа (МРА) при его испытании в полуразомкнутой магнитной системе (МС). Для построения модели был использован множественный регрессионный анализ, задача которого состоит в построении уравнения такой поверхности в трехмерном пространстве, которая располагается на минимальном расстоянии от результатов наблюдений. В результате было получено уравнение модели поверхности в трехмерном пространстве для образца из стали Э330 со всеми значащими коэффициентами и незначащим отношением остаточных дисперсий. Таким образом, проведенный эксперимент подтверждает, что изменение напряженности магнитного поля вдоль оси x от поверхности образца из магнитомягкого материала при испытаниях в полуразомкнутых магнитных системах носит нелинейный характер.

Статья в формате PDF

307 KB

топография магнитного поля

магнитная система

магнитомягкие материалы

регрессионный анализ

1. Буль, О. Б. Методы расчета магнитных систем электрических аппаратов. Магнитные цепи, поля и программа FEMM / О. Б. Буль. – М.: Академия, 2005. – 336 с.

2. Ланкин, М. В. Приборы и методы контроля магнитных свойств постоянных магнитов: монография / М. В. Ланкин; Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ (НПИ), 2007. – 292 с.

3. Ланкин, М. В. Оптимизация параметров измерительного преобразователя напряженности магнитного поля / М. В. Ланкин, Н. Д. Наракидзе // Изв. вузов. Электромеханика. – 2008. - №2. – С. 32-35.

4. Львовский, Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие для втузов / Е. Н. Львовский. – М.: Высш. шк., 1988. – 239 с.

5. Львовский, Е. Н. Пассивный и активный эксперимент при исследовании механических характеристик бетона / Е. Н. Львовский. – Кишинев: Картя Молдовеняскэ, 1988.– 176 с.

В [2] с помощью нелинейного регрессионного анализа была получена модель топографии магнитного поля (МП) постоянного магнита при его испытании в полуразомкнутой магнитной системе (МС). Для разработки метода, позволяющего измерять напряженность МП поля на поверхности изделий из магнитомягких материалов (МММ) при их испытаниях в полуразомкнутых МС, необходимо решить задачу построения математической модели изменения напряженности МП.

Такая математическая модель в случае неизменности зазора δ между полюсами намагничивающей системы (НС) и изделия из ферромагнитного материала (ФММ) и его геометрических размеров λ (λ – параметр, характеризующий геометрические размеры изделия из ФММ; λ = l/d_max, где l – длина изделия из ФММ; d_max – максимальный размер поперечного сечения изделия из ФММ) имеет вид , где х – расстояние от испытуемого образца, I – ток НС.

Для построения модели топографии МП изделия из МММ при помощи пакета Femm 4.0 [1] была рассчитана зависимость напряженности МП от тока НС и расстояния x от центра на поверхности изделия из МММ (сталь Э330) (рис. 1 и рис. 2) с размерами образцов 29×15×15 мм и зазором между полюсами НС и изделия из МММ 3 мм (λ=2; δ=3; λ/2δ=0,33).

Рис. 1. Семейство КР образца из стали Э330 при различных значениях расстояния х (мм)

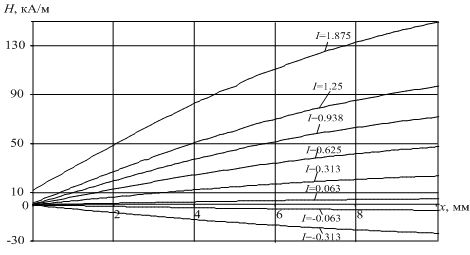
Рис. 2. Зависимость тангенциальной составляющей напряженности Hτ образца из стали Э330 от расстояния х при различных значениях тока I

Для построения модели был использован множественный регрессионный анализ (МРА). Задача МРА состоит в построении уравнения такой поверхности в трехмерном пространстве, которая располагается на минимальном расстоянии от результатов наблюдений Нi. Для определения этого расстояния воспользуемся выражением остаточной дисперсии S2ост. [4]:

,

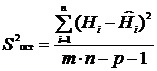где n – количество значений тока I, при которых измерялась напряженность МП Нi; m – количество точек пространства, в которых измерялась напряженность МП; р – количество слагаемых в уравнении поверхности; – расчетное значение напряженности МП, полученное из уравнения поверхности .

Для определения коэффициентов уравнения регрессии bi использовалось выражение в матричном виде [3]:

, (1)

где В – вектор-столбец коэффициентов уравнения регрессии bi; Y – вектор-столбец результатов наблюдений Hi; Х – матрица факторов, причем для определения нулевого коэффициента регрессии в нее добавляется столбец единичных значений, т.е. ,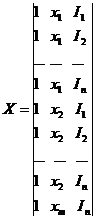

ХТ – транспонированная матрица Х, (ХТХ)-1 – матрица, обратная ХТХ.

В общем виде нелинейное уравнение регрессии можно представить как:

Обычно задачу решают за несколько шагов путем повышения степени уравнения до тех пор, пока уменьшение остаточной дисперсии остается значимым. Для расчета коэффициентов bi воспользуемся выражением (1), но, начиная со второго шага перед повышением степени полинома, будем производить замену переменных, линеаризующих функций: х12=х2, х13=х3, I12=I2, I13=I3 и так далее [4].

Момент прекращения наращивания степени полинома можно определить следующим образом. После каждой итерации проводится проверка гипотезы об отсутствии различия остаточных дисперсий и . Для этого используется критерий Фишера:

,

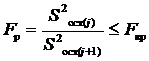где – критическое значение критерия Фишера, для числа степеней свободы , и выбранного уровня значимости % [4].

После проведения нескольких итераций (j=5) была построена модель напряженности МП вплоть до пятого порядка и рассчитаны остаточные дисперсии для образца из МММ стали Э330. Результаты вычислений сведены в табл. 1.

Таблица 1 Результаты вычислений остаточной дисперсии

График зависимости остаточных дисперсий S2ост от количества слагаемых в уравнении поверхности p для образца из стали Э330 показан на рис.3.

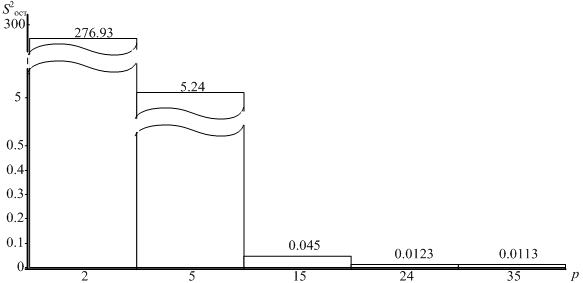
Рис. 3. Зависимость S2ост от количества слагаемых в уравнении поверхности p для образца из стали Э330

Таким образом, в качестве модели изменения напряженности МП при перемагничивании образцов из стали Э330 по кривой размагничивания (КР) может быть использовано уравнение регрессии четвертой степени:

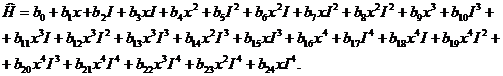
Результат вычислений коэффициентов уравнения регрессии сведен в табл. 2.

Таблица 2. Результаты вычислений коэффициентов bi (сталь Э330, tкр =1,661)

Проверка значимости полученных коэффициентов уравнения регрессии bi произведена с использованием t-критерий Стьюдента [5]:

; ,

где cii – диагональный элемент матрицы обратной к матрице нормальных уравнений (ХТХ)-1; – погрешность коэффициента регрессии.

Результаты вычислений – коэффициентов сведены в табл. 2. Из данных табл. 2 можно сделать вывод о незначимости восемнадцати коэффициентов полученного уравнения регрессии. Поэтому согласно [5], был произведен постепенный отсев незначащих коэффициентов, у которых tbi<0,5, а затем tbi<1 и, кроме того, по критерию Фишера проводилась оценка значимости отношений остаточных дисперсий. В результате такого отсева было получено уравнение модели поверхности в трехмерном пространстве для образца из стали Э330 со всеми значащими коэффициентами и незначащим отношением остаточных дисперсий (табл. 3).

Таблица 3. Результаты вычислений коэффициентов bi (сталь Э330, tкр =1,659)

После исключения незначащих коэффициентов уравнение модели для образца из стали Э330 выглядит следующим образом:

.

При подстановке bi :

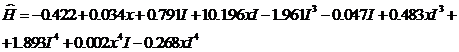
На рис. 4 показано распределение напряженности МП для образца из стали Э330, построенное с помощью полученного уравнений регрессии.

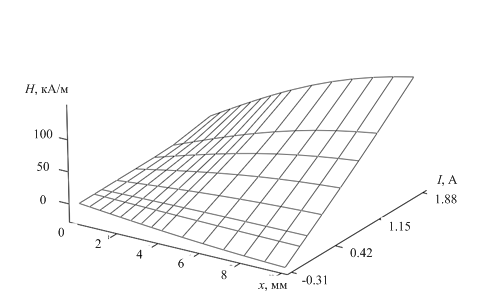
Рис. 4. Регрессионная модель распределения напряженности МП стали Э330

Таким образом, проведенный эксперимент подтвердил, что изменение напряженности МП вдоль оси x от поверхности образца из МММ при испытаниях в полуразомкнутых МС носит нелинейный характер.

Статья подготовлена с использованием оборудования ЦКП "Диагностика и энергоэффективное электрооборудование" ЮРГПУ(НПИ).

Рецензенты:

Лачин В.И., д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, г.Новочеркасск.

Гречихин В.В, д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, г. Новочеркасск.

Библиографическая ссылка