Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,039

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Болдин Б.С. 1

---

1 ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова»

В статье рассматриваются модели прогнозирования основных параметров динамической модели банка. Описываются модели временных рядов и модели множественной регрессии в целях использования их для учета изменчивости внешних экономических факторов. Приводится описание методики анализа и оценки параметров модели современными эконометрическими методами. Особое внимание уделяется анализу прогнозных оценок параметров модели, которые позволяют дать адекватную оценку планируемого результата с учетом изменяющихся во времени внешних экономических условий. Сделан вывод о возможности решения указанной задачи стандартными эконометрическими методами и приведены результаты решения, повышающие эффективность прогноза изменения параметров банка в соответствии с изменяющимися сценариями экономического развития. Указаны перспективы дальнейшего развития и применения и представленных моделей.

Статья в формате PDF

124 KB

модели временных рядов

модель множественной регрессии

динамические модели банка

динамика управления ликвидностью банка

1. Грибов А.Ф. Моделирование банковской деятельности: учебно-методическое пособие для дистанционной формы обучения. М.: Изд-во Рос. экон. акад., 2004.

2. Дорохина Е.Ю., Халиков М.А. Моделирование микроэкономики. М.: Экзамен, 2000.

3. Минько Э.В., Минько А.Э. Методы прогнозирования и исследования операций: учеб. пособие / под ред. Будагова А.С. М. : Финансы и статистика; ИНФРА-М, 2010.

4. Суровцев Л.К. Математическая экономика: учеб. пособие. М.: Экономика, 2011.

5. Синки Дж. Управление финансами в коммерческих банках. М.: Cattalaxy, 1985.

Планирование ликвидности отличается динамичностью и зависит от соотношения притока и оттока средств. Денежные потоки, связанные с управлением ликвидностью, не полностью случайные, таким образом, требования ликвидности могут быть с некоторой долей точности предсказаны заранее. Суть планирования ликвидности – прогнозировать будущий спрос на банковские кредиты, будущие поставки депозитов и изменение отношения рынка к этим видам финансовой деятельности. Формирование ожиданий и методы прогнозирования выступают важнейшими компонентами управления ликвидностью.

Три базовых элемента формируют ожидание – инерция, экстраполяция и регрессия. Первый элемент – ожидание отсутствия изменений, действие инерции. Второй – определение будущих изменений через экстраполяцию изменений в прошлом. Под действием этого фактора переменная движется вперед или назад в зависимости от прошлых изменений. Третий элемент – «возврат к нормальности». Он возвращает переменную к нормальному историческому уровню.

Допустим, в текущий период t мы хотим определить переменную X для периода t+1. Переменной может быть спрос на кредиты, поставка депозитов или процентная ставка. Формула, сочетающая три фактора ожиданий, будет выглядеть следующим образом:

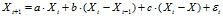, где a, b и c – параметры или коэффициенты элементов инерции, экстраполяции и регрессии соответственно; Х – историческая норма, аппроксимируемая через скользящее среднее; 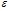– элемент случайности, отражающий влияние не учтенных в формуле переменных. Формула содержит все базовые параметры, необходимые для прогнозирования переменной на базе ее прошлых изменений. Заметим, что при a = 1 формула может быть переписана как модель предполагаемых изменений:

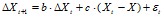
Если b = c =0, предсказываемое изменение равно нулю, то доминирует элемент инерции. Заметим, однако, что при предполагаемом значении c меньше нуля ожидается влияние фактора регрессии, которое заставит переменную вернуться к нормальному состоянию. Элемент экстраполяции удаляет переменную от текущего уровня, тогда как элемент регрессии приближает ее к исторической норме. Результаты представленной модели прогнозирования зависят от предполагаемых значений параметров a, b и c.

Стратегическое развитие Банка направлено на повышение капитализации и расширение бизнеса Банка с учетом особенностей современных экономических условий, анализ которых приведен в соответствующих разделах настоящего ежеквартального отчета.

Главной стратегической целью развития Банка является повышение конкурентоспособности и устойчивости Банка. Достижению данной цели будет способствовать:

• Активное продвижение на целевые клиентские ниши. Деятельность Банка будет осуществляться по двум направлениям: привлечение на обслуживание в Банк новых клиентов и развитие кредитных операций в сфере реального сектора российской экономики, представителей малого и среднего бизнеса.
• Развитие технологической базы.
• Развитие и совершенствование региональной сети.

Общая стратегия Банка на ближайшие 5 лет (таблица 1):

Таблица 1 (Общая стратегия банка):

Модели прогноза основных параметров деятельности банка

К основным статистическим методам, которые можно использовать для прогнозирования значений отдельных групп пассивов, можно отнести:

• Построение модели множественной регрессии значений внутренних показателей банка от внешних (макроэкономических) показателей.
• Построение моделей временных рядов.

Для успешного изучения динамики исследуемого процесса важно, чтобы информация о нем была полной, чтобы временной ряд имел достаточную длину. При попытке построения моделей временных рядов объемов депозитов физических и юридических лиц банка могут быль получены неудовлетворительные результаты – возникли трудности c интегрируемостью временных рядов и недостаточным количеством информации – точек временного ряда.

Поэтому для успешной реализации описанной динамической модели прогноз основных ее параметров проведем следующим образом:

1. С помощью методов оценки параметров множественной регрессии построим уравнения зависимости объемов отдельных групп пассивов банка от макроэкономических показателей.
2. Определим основные сценарии изменения макроэкономических показателей и через эконометрические уравнения определим прогнозные значения объемов пассивов.

При этом будем считать, что структура основных групп прогнозируемых показателей не изменяется во времени – таким образом, облегчая прогнозирования пассивов в разбивке по группам срочности. Аналогично поступим при прогнозировании процентных ставок. Опишем все процентные ставки – по всем группам пассивов и активов, во всех группах срочности следующим выражением: r_ij = r_цб + ∆_ij, где r_цб - ставка рефинансирования Центрального Банка РФ, а ∆_ij - разность между процентной ставкой в данной группе показателей и ставкой рефинансирования. Будем считать, что ∆_ij  постоянна в рассматриваемом временном интервале. Тогда прогнозирование процентных ставок сводится к определению возможных значений ставки рефинансирования.

Опишем процесс построения основных уравнений регрессии.

Рассмотрим следующие переменные:

Х₁ - Индекс потребительских цен, в % к декабрю предыдущего года;

Х₂ - Реальные располагаемые денежные доходы;

Х₃ - Общий уровень безработицы, % к экономически активному населению, на конец периода;

Х₄ - Расходы на покупку товаров и услуг;

Х₅ - Цена на нефть сорта "Юралс", долларов США за баррель;

Х₆ - Официальный курс рубля к доллару США, рублей за доллар США;

Y - Объем депозитов физических лиц.

Первоначальное решение о включении или не включении отдельных факторов в модель будем принимать, основываясь на значениях линейных коэффициентов парной и частной корреляции. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели.

Многофакторный анализ проведем с использованием пакета Statgraphics.

Коэффициенты парной корреляции (таблица 2):

Коэффициенты частной корреляции (таблица 3):

Для построения модели многофакторной регрессии используется пункт меню Multiple Regression. Получено следующее уравнение:

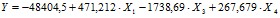
Оценка параметров модели (таблица 4):

Дисперсионный анализ (таблица 5):

Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента. Выдвигается гипотеза Н0 о статистически незначимых отличиях параметров модели от нуля. Фактическое значение t-статистики для всех параметров модели выше табличного, поэтому гипотезу Н0 можно отклонить. Таким образом, все оценки параметров модели статистически значимы.

Значение скорректированного нескорректированного линейных коэффициентов множественной детерминации приведено в таблице в рамках регрессионной статистики.

Нескорректированный коэффициент детерминации 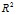= 93,61% оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Таким образом, вариация Y на 93, 61 % объясняется вариацией факторов Х1, Х3, Х4. На долю прочих факторов, не учитываемых в модели, приходится 6,39 %.

Скорректированный коэффициент множественной детерминации 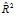=93,02 % определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом переменных.

Вывод:

Оба коэффициента указывают на достаточно высокую (более 90 %) детерминированность результата Y в модели факторами Х₁, Х₃, Х₄.

По данным таблицы дисперсионного анализа F_факт = 156,38. Вероятность случайно получить такое значение F-критерия Фишера составляет 0,0000, что не превосходит допустимый уровень 5 % – об этом свидетельствует величина P-значения из той же таблицы. Следовательно, полученное значение не случайно – оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения.

Рецензенты:

Тихомирова Е.И., д.э.н., профессор, декан факультета математической экономики и информатики ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.

Зинчук Г.М., д.э.н., доцент, декан Общеэкономического факультета ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.

Библиографическая ссылка