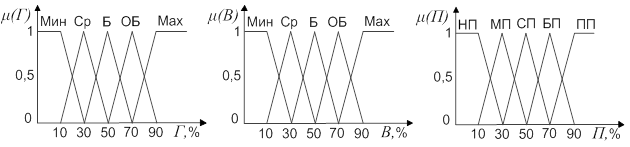Введение
Одним из требований к современной технологии лесопользования является обеспечение на лесосечных работах минимального повреждения компонентов формируемого в процессе выборочных рубок насаждения и в том числе деревьев, оставляемых на доращивание. Беспрепятственная валка дерева и сохранения подроста обеспечивается наличием свободной площадки (просвета) между деревьями, оставляемыми на доращивание. Расчетные геометрические размеры такой площадки должны учитывать параметры вырубаемого дерева.
Традиционно подобные задачи решались вероятностными методами, и учитывался только один параметр – размер по горизонтали (диаметры крон), но в работе [2] было обосновано, что для такого класса задач применение методов теории нечетких множеств является более корректным подходом. К этому нужно добавить, что для большей точности следует учитывать не только размеры по горизонтали, но и в вертикальной плоскости (высоту крон). Поскольку в комплексе такие вопросы ранее не рассматривались, то задача оставалась нерешенной.
Целью настоящей работы являлось получение функциональной зависимости возможных повреждений деревьев и их величины от степени пересечения крон в горизонтальной и вертикальной плоскостях на основе нечеткого вывода.
Достижение поставленной цели предусматривало решение следующих задач.
1. Выполнение содержательной постановки задачи нечеткого вывода возможных повреждений деревьев при повале.
2. Выполнение практической реализации задачи нечеткого вывода.
3. Синтез нечеткой модели возможных повреждений деревьев при повале средствами FuzzyLogicToolbox.
Содержательная постановка задачи
Содержательная постановка задачи заключается в описании взаимодействия крон деревьев при повале. Процесс появления возможных повреждений зависит от степени пересечения крон в двух плоскостях: горизонтальной, определяемой диаметром крон, и вертикальной, определяемой высотой крон. При этом нужно учитывать специфику взаимодействия. Так, при минимальном перекрытии крон по диаметру надо полагать, что повреждения будут также минимальными независимо от степени перекрытия крон по вертикали. Аналогичная картина будет наблюдаться и при минимальном перекрытии крон по вертикали.
При другом крайнем значении перекрытия - максимальном, как в вертикальном, так и горизонтальном, степень повреждений будет пропорциональна изменению другого варьируемого значения перекрытия крон.
При максимальных значениях перекрытия крон в обеих плоскостях повреждения будут также однозначно максимальными, так как этот вариант соответствует касательному соударению стволов деревьев. Таким образом, используя описательное содержание вариантов взаимодействия крон, можно формализовать все основные правила нечеткого вывода повреждений при повале.
Практическая реализация задачи нечеткого вывода
Определение входных и выходных переменных задачи (приведение к нечеткости). Входными величинами задачи принимаются в процентном отношении степень перекрытия крон по горизонтали и степень перекрытия крон по вертикали. Выходной величиной является повреждение кроны.
Определим нечеткие функции принадлежности условий повала деревьев. Во многих случаях при решении подобных задач [3; 4] на универсуме нечеткого множества принимают минимальное значение функции принадлежности, равное трем, что позволяет обойтись небольшим объемом базы правил. Но в таких случаях, в зависимости от размерности параметров, выходная величина аппроксимируется менее гладкой, ступенчатой функцией. Для повышения точности рекомендуется увеличивать количество значений каждой лингвистической переменной и принимать их в диапазоне от 3 до 7 [1]. В данном случае будет наиболее рационально принять пять значений входных и выходной лингвистических переменных.
На рисунках 1а, 1б показаны функции принадлежности входных переменных в виде треугольных нечетких чисел и трапецеидальных интервалов, а на рисунке 1в приведена нечеткая функция лингвистической переменной «Повреждения». В качестве обозначений лингвистических переменных для предложенных функций приняты следующие значения: Мин - минимальный; Ср - средний; Б - большой; ОБ - очень большой; Мах -максимальный; НП - нет повреждений; MП - малые повреждения; СП - средние повреждения; БП - большие повреждения; ПП - полное повреждение.
В терминах теории нечетких множеств лингвистические переменные определены терм-множествами со следующие значениями:
- «Степень перекрытия крон по горизонтали, Г» {Мин, Ср, Б, ОБ, Мах};
- «Степень перекрытия крон по вертикали, В» {Мин, Ср, Б, ОБ, Мах};
- «Повреждения, П» {НП, MП, СП, БП, ПП}.
Будем полагать, что терм-множества значений лингвистических переменных представлены треугольными нечеткими числами, а на границах области определения трапецеидальными нечеткими интервалами (рисунок 1)
|
|
||
|
а) |
б) |
в) |
Рисунок 1 – Нечеткие функции принадлежности лингвистических переменных
а - «Степень перекрытия крон по горизонтали, Г»; б - «Степень перекрытия крон по вертикали, В»; в - «Повреждения, П»
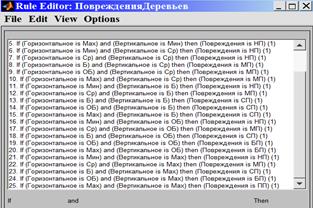
Формирование базы правил системы нечеткого вывода. Составим базу правил нечеткой продукции в матричной форме (таблица 1).
Таблица 1 – Состав базы правил нечеткой продукции для вывода функции принадлежности
|
Значения лингвистической переменной «Г» |
Значения выходных нечетких подмножеств «Повреждения» при изменении нечеткой функции «В» |
||||
|
Мин |
Ср |
Б |
ОБ |
Мах |
|
|
Мин |
НП |
НП |
НП |
НП |
НП |
|
Ср |
НП |
НП |
МП |
МП |
МП |
|
Б |
НП |
МП |
СП |
СП |
СП |
|
ОБ |
НП |
МП |
СП |
БП |
БП |
|
Мах |
НП |
МП |
СП |
БП |
ПП |
Синтез нечеткой модели
Изложенная формальная постановка задачи нечеткого вывода позволяет реализовать ее в специализированных компьютерных программах.
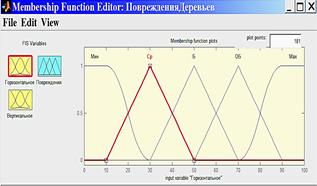
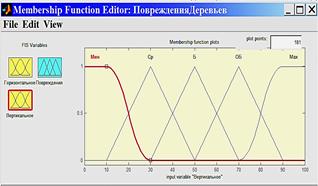
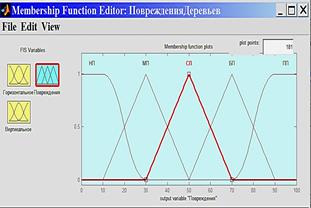
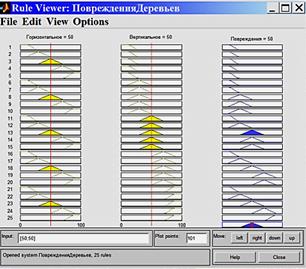
Реализация задачи нечеткого вывода выполнена в среде FISEditor (рисунок 2) приложения MatLabFuzzyLogicToolbox[5]. В данном случае использовался алгоритм по известной [3-5] методике.
1. Фаззификация (введение нечеткости), (рисунки 2а-2в).
2. Формирование базы правил нечеткой продукции (рисунок 2г).
3. Нечеткий вывод (рисунок 2д).
4. Дефаззификация (приведение к четкости), (рисунок 2д).
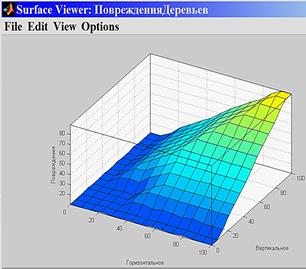
5. Получение функции нечеткого вывода (рисунок 2е).
|
а) |
б) |
|
в) |
г) |
|
д) |
е) |
Рисунок 2 – Нечеткий вывод в среде FISEditor приложения MatLabFuzzyLogicToolbox
а - нечеткая функция принадлежности переменной «Г»; б - нечеткая функция принадлежности переменной «В»; в - нечеткая функция принадлежности лингвистической переменной «П»; г - база правил нечеткого вывода; д - процедура нечеткого вывода и приведения к четкости; е - функция нечеткого вывода.
Выводы
Проведенные исследования позволяют сделать следующие выводы.
1. Использование вероятностных методов для оценки поврежденности деревьев при повале является недостаточно корректным подходом. Для такого класса задач в наибольшей степени подходят методы, основанные на теории нечетких множеств.
2. Предлагаемая функция возможных повреждений, построенная на основе нечеткого вывода, учитывает степень пересечения крон по диаметру и высоте.
3. Полученная функция возможных повреждений может использоваться для нечеткого моделирования процессов лесосечных работ с оценкой возможных повреждений при валке деревьев.
Рецензенты:
Гороховский Александр Григорьевич, доктор технических наук, профессор, генеральный директор ОАО «Уральский научно-исследовательский институт переработки древесины», г. Екатеринбург.
Баженов Евгений Евгеньевич, доктор технических наук, профессор, директор института автомобильного транспорта и технологических систем ФГБОУ ВПО «УГЛТУ», г. Екатеринбург.
Библиографическая ссылка
Побединский В.В., Герц Э.Ф., Рябкова Н.В. НЕЧЕТКИЙ ВЫВОД ВОЗМОЖНЫХ ПОВРЕЖДЕНИЙ ДЕРЕВЬЕВ ПРИ ПОВАЛЕ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=8932 (дата обращения: 20.04.2024).