Введение
В современных условиях для нормальной работы энергосистемы и ее подразделений существует проблема получения прогнозных оценок суточных, месячных, сезонных и годовых графиков электрических нагрузок. График электрической нагрузки и его форма определяют количество и мощность генерирующих источников, работающих в базовом и пиковом режиме, состав основного технологического оборудования, параметры характерных режимов. Прогноз нагрузок позволяет планировать режимы работы энергосистемы.
Планирование режимов осуществляется на основе данных энергетических объектов за предыдущие периоды (ретроспектива), а также на основе прогноза нагрузки на перспективный период. Статистическая информация получается на основе данных телеизмерений режимных параметров, а также по результатам контрольных замеров для характерных точек энергосистемы (подстанций) в рабочие и выходные дни.
Существует большое количество моделей и методов прогнозирования нагрузки. Они могут быть классифицированы как модели временных рядов, в которых нагрузка моделируется как функция ее наблюдаемых в прошлом значений, и причинные модели, в которых нагрузка моделируется как функция некоторых экзогенных факторов, особенно погодных и социальных. Некоторые из первых моделей являются мультипликативными авторегрессионными, динамическими линейными или нелинейными моделями, пороговыми авторегрессионными, построенными на фильтрах Кальмана. Вторые, как правило, являются передаточными функциями Бокса и Дженкинса, моделями ARMAX, оптимизационными моделями, моделями непараметрической регрессии и др.
В последнее время с развитием теории искусственного интеллекта решение задачи прогнозирования нагрузки осуществляют с использованием моделей на основе искусственных нейронных сетей (ИНС).
Альтернативным вариантом является применение для прогнозирования ИНС в сочетании с элементами нечеткой логики (так называемые нечеткие гибридные нейронные сети).
Система нечеткого вывода
Элементы теории нечетких множеств, правила импликации и нечетких рассуждений образуют систему нечеткого вывода. В ней можно выделить:
- множество используемых нечетких правил;
- базу данных, содержащую описания функции принадлежности;
- механизм вывода и агрегирования, который формируется применяемыми правилами импликации.
В случае технической реализации в качестве входных и выходных сигналов выступают измеряемые величины, однозначно сопоставляющие входным значениям соответствующие выходные значения.
Для обеспечения взаимодействия этих двух видов вводится нечеткая система с так называемым фазификатором (преобразователем множеств входных данных в нечеткое множество на входе) и дефазификатором (преобразователем нечетких множеств в конкретное значение выходной переменной) на выходе.
Фазификатор преобразует точное множество входных данных в нечеткое множество, определенное с помощью функции принадлежности, а дефазификатор решает обратную задачу – формирует однозначное решение относительно входной переменной на основании многих нечетких выводов, вырабатываемых исполнительным модулем нечеткой системы.
Выходной сигнал модуля вывода может иметь вид М нечетких множеств, определяющих диапазон измерения выходной переменной. Дефазификатор преобразует этот диапазон в одно конкретное значение, принимаемое в качестве выходного сигнала всей системы.
Наибольшей популярностью для фазификации пользуются функции принадлежности гауссовского типа, треугольные и трапецеидальные функции [5].
Далее представлена методика краткосрочного прогнозирования на основе использования нечетких ИНС.
Описание методики
В качестве базовой модели нечеткого логического вывода будем использовать модель вывода типа Сугено. Исходными данными будут значения электрических нагрузок, полученные за сутки с интервалом 15 минут. В качестве инструмента для моделирования был выбран пакет Fuzzy Toolbox Matlab.
Нечеткий логический вывод Сугено [4] выполняется по следующей нечеткой базе знаний:
![]()
![]()
![]()
![]()
![]() …
…![]()
![]()
![]() ,
, ![]() , (1)
, (1)
где ![]() – некоторые действительные числа.
– некоторые действительные числа.
Правила в базе Сугено задаются линейной функцией от входов
![]() (2)
(2)
Методика прогнозирования согласно [2] включает в себя следующие этапы:
1. Создание обучающей выборки электрических нагрузок, состоящей из четырех входных переменных и одной выходной переменной. Первая входная переменная – электрическая нагрузка в текущее время, вторая входная переменная – электрическая нагрузка на 15 минут раньше, третья входная переменная – электрическая нагрузка на 30 минут раньше, четвертая переменная – электрическая нагрузка на 45 минут раньше. Выходная переменная – электрическая нагрузка через 15 минут от текущего времени.
2. Загрузка обучающей выборки в редактор ANFIS. Внешний вид редактора ANFIS с загруженными данными представлен (скриншот) на рисунке 1.
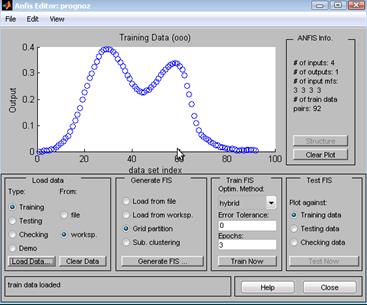
Рис. 1. Графический интерфейс редактора ANFIS после загрузки обучающих данных в системе Fuzzy Toolbox Matlab
3. Задание для каждой входной переменной по 3 лингвистических терма, типа функции принадлежности входных данных (треугольная) и типа функции принадлежности для выходной данной (линейная). Задание количества и типов функций принадлежности в системе Fuzzy Toolbox Matlab представлены (скриншот) на рисунке 2.
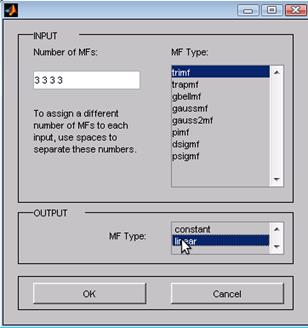
Рис. 2. Задание количества и типов функций принадлежности в системе Fuzzy Toolbox Matlab
Треугольная функция принадлежности имеет вид:
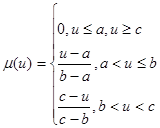 (3)
(3)
где (a,c) - носитель нечеткого множества – пессимистическая оценка нечеткого числа; b – координата максимума – оптимистическая оценка нечеткого числа [4].
4. Обучение гибридной сети с уровнем ошибки 0 и количеством циклов обучения равным 60.
5. График зависимости ошибки обучения от количества циклов обучения в системе Fuzzy Toolbox Matlab представлен (скриншот) на рисунке 3.
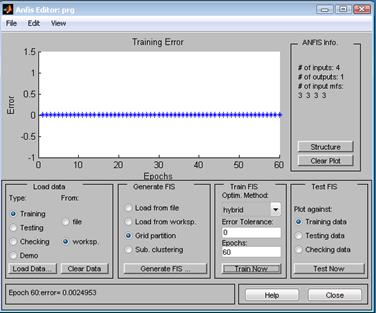
Рис. 3. График зависимости ошибки обучения от количества циклов обучения в системе Fuzzy Toolbox Matlab
6. Визуальная оценка структуры построенной нечеткой модели. Структура сгенерированной системы нечеткого вывода представлена (скриншот) на рисунке 4.
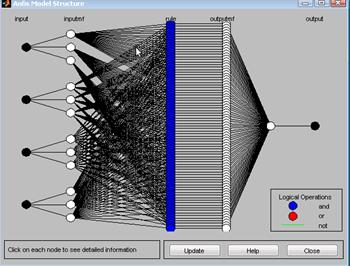
Рис. 4. Структура сгенерированной системы нечеткого вывода
7. Проверка адекватности построенной нечеткой модели гибридной сети представлена (скриншот) окном с отображением результата на рисунке 5.
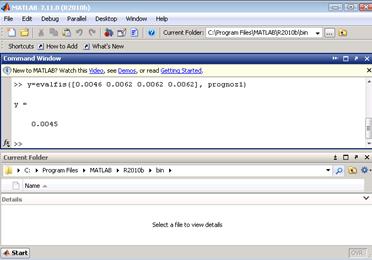
Рис. 5. Окно с отображением результата оценки построенной нечеткой модели гибридной сети
Заключение
В результате проделанной работы было:
1) Разработана методика прогнозирования на основе нечеткой нейронной сети.
2) Базовой моделью нечеткого логического вывода, используемой в методике, является модель нечеткого вывода типа Сугено.
3) В качестве функции принадлежности входных переменных использована треугольная функция.
4) Созданная нечеткая нейронная сеть позволяет получать краткосрочный прогноз нагрузки с точностью 0,003.
В данном исследовании не рассматривались вопросы предварительной обработки данных, анализа главных компонент, а также вопросы со значимостью входных параметров. Проблема определения размерности может быть решена при помощи использования алгоритма «Bokskaunting».
Рецензенты:
Атрощенко Валерий Александрович, доктор технических наук, профессор, декан факультета компьютерных технологий и автоматизированных систем, ФГБОУ ВПО «Кубанский государственный технологический университет» (Министерство образования и науки РФ), г. Краснодар.
Шевцов Юрий Дмитриевич, доктор технических наук, профессор кафедры Информатики, ФГБОУ ВПО «Кубанский государственный технологический университет» (Министерство образования и науки РФ), г. Краснодар.
Библиографическая ссылка
Сахно Е.П., Дьяченко Р.А., Решетняк М.Г., Капустин К.Ю. К ВОПРОСУ КРАТКОСРОЧНОГО ПРОГНОЗИРОВАНИЯ ЭЛЕКТРИЧЕСКИХ НАГРУЗОК С ПРИМЕНЕНИЕМ НЕЧЕТКИХ НЕЙРОННЫХ СЕТЕЙ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=8745 (дата обращения: 20.04.2024).



