Значительное повышение конструктивной сложности современных технических систем требует необходимости своевременного и точного диагностирования качества их работы. Техническая диагностика благодаря возможности раннего обнаружения дефектного состояния объекта позволяет устранить отказы в процессе технического обслуживания или нормального функционирования, что повышает надежность и долговечность как отдельных элементов, так и всей механической системы в целом. Увеличение мощностей, быстродействия, скоростей и других характеристик механической системы приводит к возникновению больших динамических нагрузок и упругих колебаний и, в результате, к значительному количеству отказов. Поэтому вопросы долговечности и надежности таких систем в условиях воздействия вибраций приобретают решающее значение.
В конце 20-го века в качестве отдельного направления технической диагностики выделились виброакустическая и вибрационная диагностика.
На протяжении долгого времени большинство исследований в области технической вибродиагностики было нацелено на решение линейных динамических задач, которые математически описываются системой линейных дифференциальных уравнений. Достигнутые при этом успехи в значительной мере были обусловлены тем, что в соответствующих практических приложениях оказались оправданными принципиальные упрощения линейной теории колебаний.
Однако во многих случаях линейные математические модели принципиально не способны отобразить истинное динамическое поведение конструкции. Поэтому попытка строить процедуру вибродиагностики на основе линеаризованных моделей может привести к качественно и количественно неверным результатам. Кроме того, линейные методы вибродиагностики имеют и ряд других недостатков (низкая чувствительность к возникающим дефектам; ограниченное количество параметров колебаний, которые могут использоваться в качестве диагностических признаков; необходимость наличия эталонного неповрежденного объекта и др.), ограничивающих область их практического применения.
В этих условиях было признано целесообразным перейти к развитию нелинейной вибродиагностики, базирующейся на использовании нелинейных математических моделей объектов контроля и нацеленной на создание новых, более совершенных методов и средств поиска дефектов. Основные подходы и задачи нелинейной вибродиагностики сформулированы в [5,6,7].
Эффективность диагностических процедур нелинейной вибродиагностики может быть значительно повышена путем оптимизации тестового воздействия или варьируемых параметров самой динамической системы для достижения наилучшей чувствительности и точности. То, что это становится возможным, подчеркивает эффективность подходов нелинейной вибродиагностики в сравнении с традиционными методами, обеспечивает возможность управления ходом диагностических процедур для достижения оптимальных результатов по точности и чувствительности.
Использование теории чувствительности для анализа и синтеза сложных механических систем детально рассмотрено в [2], где также представлен подробный аналитический обзор отечественных и зарубежных публикаций по данной теме.
При решении задачи диагностирования функция чувствительности диагностического признака П к изменению контролируемого параметра q (например, коэффициента жесткости или диссипации) определяется выражением
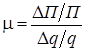, (1)
где ∆П – абсолютное изменение диагностического признака П, соответствующее абсолютному изменению контролируемого параметра q на величину ∆q.
Из анализа выражения (1) следует, что, если относительное изменение отклика (диагностического признака П) численно равно относительному изменению контролируемого параметра q, то чувствительность диагностического метода равна единице (µ=1). При разработке диагностических процедур или при оптимизации тестовых воздействий следует стремиться к достижению максимально возможных значений функции чувствительности. Это позволит получать более достоверные и качественные результаты вибрационного контроля даже при использовании достаточно «грубой» и более дешевой контрольно-измерительной аппаратуры.
Использование функции чувствительности (1) вследствие её безразмерности позволяет сравнивать различные диагностические методы и алгоритмы между собой и выявлять наиболее предпочтительные диагностические признаки по критерию максимальной чувствительности к возникающему дефекту.
Для возможности исследования поведения функции чувствительности при изменении параметров тестового воздействия (например, амплитуды и частоты гармонической вынуждающей силы) или собственных параметров диагностируемого объекта вместо выражения (1) возможно использовать выражение частной производной функциональной зависимости информативного признака П по контролируемому параметру qi:
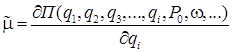. (2)
Рассмотрим порядок повышения точности и чувствительности процедуры нелинейной вибродиагностики на примере метода [1] идентификации сухого трения при вынужденных колебаниях динамической системы (рис.1) по «скачку» на виброграмме ускорения (рис.2–3). Причем на рис. 2 представлены графики, полученные с помощью компьютерного математического моделирования динамики рассматриваемой системы в среде Simulink/MATLAB [3], а на рис. 3 – экспериментальная виброграмма ускорения реальной колебательной системы с сухим трением.
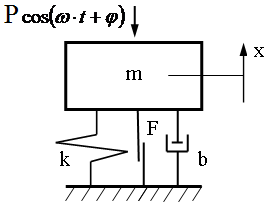
Рис.1 Расчетная динамическая схема системы с сухим трением
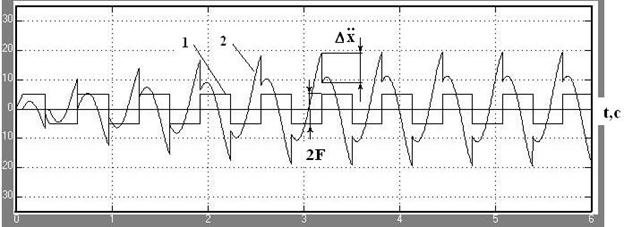
Рис. 3. Виброграмма ускорения (2) и график (1) изменения силы сухого трения во времени системы с сухим трением при безостановочном режиме движения (
с-1, F=5Н, P= =8Н, b=0.12 Нc/м, k=36Н/м, m=0.5 кг)
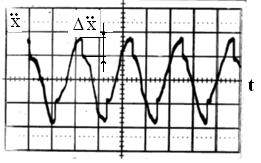
Рис. 5. Экспериментальная осциллограмма виброускорения динамической системы с сухим трением
Используя количественную обусловленность величины скачка ускорения силой сухого трения при безостановочных режимах движения [4,7]:
(3)
представляется возможным определить силу сухого трения, действующую в колебательной системе:
. (4)
Функция чувствительности решающего алгоритма:
(5)
является гиперболической функцией массы колебательной системы. Следовательно, метод идентификации силы сухого трения будет тем чувствительней, чем меньше масса идентифицируемого объекта.
Оценка предельной абсолютной погрешности функции нескольких переменных 
определяется выражением [4]:
,
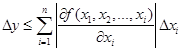где 
– абсолютные погрешности аргументов.
Для рассматриваемого метода оценку основной предельной абсолютной погрешности можно получить с помощью следующего выражения:
, (6)
или
(7)
где 
– абсолютные погрешности измерения соответственно массы колебательной системы и скачка виброускорения.
Из анализа (7) следует, что наибольшая точность 
будет достигаться при
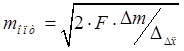, (8)
На практике принято погрешности измеряемых величин характеризовать относительными значениями, выраженными в процентах. В рассматриваемом случае 
.
В качестве примера пусть 
(кг); 
(м/c2); F=0.7 (Н).
Тогда в соответствии с (8)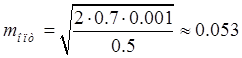 
(кг).
Соответствующая этой массе колебательной системы минимальная предельная относительная погрешность будет равна 
.
На рис. 2 представлен график зависимости предельной относительной погрешности
определения силы сухого трения по скачку виброускорения 
от массы m колебательной системы.
Рис. 2. График зависимости предельной относительной погрешности определения силы сухого трения F по скачку виброускорения от массы m колебательной системы
Таким образом, при возможности варьирования массы m колебательной системы до оптимального значения (8) будет достигнута наибольшая точность идентификации силы сухого трения F, причём при неоптимальных значениях массы m относительная погрешность может существенно возрастать (в разы) и превышать 20–30 %.
Выводы
1. Методы нелинейной вибродиагностики, в частности, определения сил сухого трения в динамических системах обладают возможностью существенного повышения чувствительности и точности за счёт выбора оптимальных параметров тестовых воздействий или варьируемых параметров самой динамической системы и обеспечивают реализацию диагностической процедуры с максимальной эффективностью.
2. Рассмотренный метод идентификации силы сухого трения в колебательной системе по «скачку» виброускорения обладает следующими достоинствами: 100 % точностью решающего алгоритма; возможностью значительного увеличения чувствительности и уменьшения предельной погрешности, инвариантностью к действующим силам вязкого сопротивления; возможностью идентификации при неполноте информации о виде вибровозбуждения; нетребовательностью к источнику возбуждения колебаний; простотой аппаратурной реализации; высокой оперативностью и производительностью идентификации вплоть до возможности организации процедуры в реальном масштабе времени.
Рецензенты:
Кобелев Н. С., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжения и вентиляция» Юго-Западного государственного университета, г. Курск.
Локтионова О. Г., д.т.н., профессор, начальник Управления подготовки и аттестации кадров высшей квалификации Юго-Западного государственного университета, г. Курск.
Библиографическая ссылка
Лушников Б.В. ОПТИМИЗАЦИЯ ПРОЦЕДУР НЕЛИНЕЙНОЙ ВИБРОДИАГНОСТИКИ СИЛЫ СУХОГО ТРЕНИЯ В ДИНАМИЧЕСКОЙ СИСТЕМЕ ПО КРИТЕРИЯМ ТОЧНОСТИ И ЧУВСТВИТЕЛЬНОСТИ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=8479 (дата обращения: 24.04.2024).