Процесс взаимодействия человека с ЭВМ стал одним из наиболее важных вопросов развития компьютерной техники с момента появления самих ЭВМ. Сначала технологи «общались» с ней через посредника-программиста. Затем был диалоговый интерфейс, после графический. Но человечество всегда искало более простое, удобное, естественное решение.
Поэтому нетрудно понять, что голосовой интерфейс - это тема, которая на протяжении последних пятидесяти лет привлекает внимание ученых и инженеров всего мира. Голосовой интерфейс на языке пользователя - это наилучшее решение. Действительно, ведь речь - это наиболее натуральная, удобная, эффективная и экономичная форма человеческого взаимодействия. Первые конкретные шаги в данной области были предприняты в 1971 году по заказу министерства обороны США [1].
В связи с быстрым и постоянным развитием как науки, так и самой жизни человека, понятия скорость и время становятся все более значимыми. Бурный рост информационных технологий позволил несколько снизить время, затрачиваемое на передачу и обработку информации. И на первый план стали выходить понятия точности, достоверности и надежности этой информации.
В системах автоматического распознавания речи важнейшим показателем является точность распознавания слитной речи, которая определяется отношением количества верно распознанных слов к сумме всех распознаваемых слов, пропущенных слов и лишних (неверно распознанных) слов [5].
В настоящее время, этот показатель стремиться к значению 95 и выше процентов.
Повышение указанного показателя является важной и актуальной задачей. Подтверждением этого могут служить:
1) множество научно-исследовательских центров, объединенных в Международную Ассоциации Речевого Взаимодействия (International Speech Communication Association);
2) научно-технические конференции, крупнейшей из которых является ежегодная Interspeech;
3) различные программно-технические разработки (Dragon Naturally Speaking, IBM Via Voice, встроенное речевое управление в ОС Vista).
Следует выделить 2 аспекта, в которых ведутся исследования, связанные с повышением точности распознавания: аппаратный и программный. В данной работе нами уделено внимание лишь алгоритмам распознавания, которые являются частью программного аспекта. Все существующие ныне основные алгоритмы могут быть группированы следующим образом:
1. Распознавание на основе СММ - скрытых марковских моделей.
2. Распознавание на основе нейросети.
3. Гибридные модели.
Каждая из них имеет свои достоинства и недостатки. Прежде всего, это обусловлено конкретными задачами и местом применения. Но большинство исследователей отдают предпочтение скрытым марковским моделям. Таким образом, задачей исследования является модификация алгоритмов распознавания речи, основанных на СММ, для повышения точности распознавания. Базовые принципы алгоритмов распознавания речи были сформулированы начале 80-х годов прошлого столетия Л. Рабинером и Р. Шафером в книге «Цифровая обработка речевых сигналов» [1]. А в качестве опубликованных исследований о трудоемкости алгоритмов распознавания речи можно выделить только статью сотрудников компании SPIRIT из журнала «Цифровая обработка сигналов» [2].
Наблюдаемая марковская модель. Рассмотрим систему, которая в произвольный момент времени может находиться в одном из N различных состояний ![]() . В дискретные моменты времени система претерпевает изменение состояния (возможно, переходя при этом опять в тоже состояние) в соответствии с некоторым вероятностным правилом, связанным с текущим состоянием. Моменты времени, в которые происходит изменение состояния системы, будем обозначать через t = 1, 2, ..., T, а ее состояние в момент времени t через qt. Полное вероятностное описание такой системы будет, вообще говоря, требовать задания как текущего состояния (в момент времени t), так и всех предыдущих. Для частного случая дискретной цепи Маркова первого порядка это вероятное описание требует знания только текущего и предыдущего состояний, т.е. сводится к виду [6]:
. В дискретные моменты времени система претерпевает изменение состояния (возможно, переходя при этом опять в тоже состояние) в соответствии с некоторым вероятностным правилом, связанным с текущим состоянием. Моменты времени, в которые происходит изменение состояния системы, будем обозначать через t = 1, 2, ..., T, а ее состояние в момент времени t через qt. Полное вероятностное описание такой системы будет, вообще говоря, требовать задания как текущего состояния (в момент времени t), так и всех предыдущих. Для частного случая дискретной цепи Маркова первого порядка это вероятное описание требует знания только текущего и предыдущего состояний, т.е. сводится к виду [6]:
![]() (1)
(1)
В дальнейшем мы будем рассматривать такие процессы, для которых правая часть в (1) не зависит от времени. В этом случае переходные вероятности aij определяются выражением:
![]() (2)
(2)
где ![]() и обладают следующими свойствами:
и обладают следующими свойствами: ![]() ,
, ![]() , поскольку удовлетворяет обычным вероятностным ограничениям.
, поскольку удовлетворяет обычным вероятностным ограничениям.
Описанный выше стохастический процесс может быть назван наблюдаемой марковской моделью, так как выходом такого процесса в каждый момент времени является очередное состояние модели, которое соответствует физическому (наблюдаемому) событию.
Поясним описанную конструкцию на примере. Рассмотрим СММ, обладающую тремя состояниями и предназначенную для моделирования погоды. Предполагается, что раз в день (например, в полдень) состояние погоды описывается одной (и только одной) из следующих характеристик:
(1) состояние 1: осадки;
(2) состояние 2: облачно;
(3) состояние 3: ясно.
Матрица А, составленная из вероятностей перехода между состояниями, имеет вид:
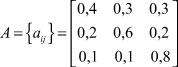 (3)
(3)
Пусть известно, что день 1-й (t = 1) - ясный (т.е. имеем состояние 3). Можно задать следующий вопрос: какова вероятность (в соответствии с заданной моделью) того, что в последующие 5 дней последовательность состояний погоды будет иметь вид: «ясно-облачно-осадки-осадки-ясно-ясно»?
Таким образом, задана последовательность наблюдений ![]() , соответствующая моментам времени t = 1, 2, ..., 6, и нужно определить вероятность появления этой последовательности для данной модели. Используя формулу Байеса и формулу (2) эта вероятность может быть записана и вычислена с помощью выражения:
, соответствующая моментам времени t = 1, 2, ..., 6, и нужно определить вероятность появления этой последовательности для данной модели. Используя формулу Байеса и формулу (2) эта вероятность может быть записана и вычислена с помощью выражения:
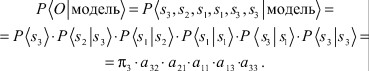 (4)
(4)
Т.е. ![]() , где
, где ![]() - вероятность того, что начальное состояние 3 (т.е. ясно).
- вероятность того, что начальное состояние 3 (т.е. ясно).
Плотность длительности состояний. Другой не менее важный и интересный вопрос звучит следующим образом: пусть модель находится в некотором известном состоянии. Какова вероятность того, что она останется в этом состоянии ровно d моментов времени? Эта вероятность может быть вычислена как вероятность последовательности наблюдений
![]() ,
,
из которой, с учетом введенной модели (т.е. формулы (4)) получаем:
![]() (5)
(5)
Величина ρi(d) есть не что иное, как дискретная функция плотности вероятности пребывания в течение времени d в состоянии i. Эта функция имеет вид показательной и представляет собой характеристику длительности данного состояния в СММ. Используя ρi(d), нетрудно вычислить ожидаемое число повторений одного и того же состояния (то есть математическое ожидание времени непрерывного пребывания в этом состоянии):
![]() (6)
(6)
Так, согласно принятой модели, наиболее вероятное число следующих друг за другом ясных дней равно ![]() , облачных - 2,5 и осадками - 1,67.
, облачных - 2,5 и осадками - 1,67.
Возможно, основной недостаток обычных СММ обусловлен используемым в них способом моделирования длительности состояний [6]. Как было показано (5), плотность вероятности ρi(d) пребывания в состоянии si с переходной вероятностью aii имеет вид показательной функции. Однако для большинства физических сигналов такая плотность вероятности для длительности пребывания в состоянии (т.е. плотность длительности состояния) является неприемлемой. Вместо этого длительность состояния многие исследователи считают нужным моделировать явно, в том или ином аналитическом виде. Рис. 1 и рис. 2 иллюстрируют (для одной из пар состояний модели si и sj) различия между СММ, с явно и неявно заданными функциями плотности длительности
состояний.
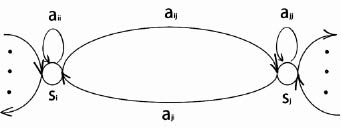
Рис. 1. СММ, в которой функции плотности длительности состояний имеют вид
прерывистых показательных
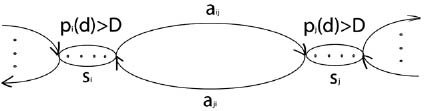
Рис. 2. СММ, в которой функции плотности длительности состояний заданы явно
На рис. 1 эти состояния имеют плотности длительности вида (5), полученные соответственно по переходным вероятностям aii и ajj. На рис. 2 коэффициенты таких вероятностей «перехода в себя» установлены равными 0, и заданы явные функции плотности длительности состояний. В этом случае переход из некоторого состояния осуществляется только после того, как будет порождено столько наблюдений, сколько их было определено в соответствии с функцией плотности длительности этого состояния. Число этих переходов задано как D.
Целесообразность введения явного описания для плотностей длительностей состояний подтверждается тем, что для многих задач это значительно улучшает качество моделирования, а, значит, и качество распознавания. Получается, что мы некоторым образом нормируем каждое состояние. Подобные подходы уже не раз показывали свою пригодность. Так в 1960 году Динез и Мэтьюз ввели концепцию временной нормализации [1].
Однако подобной модели присущи и недостатки. Одним из них является значительный рост вычислений, обусловленный введением изменяющихся длительностей состояний, что следует непосредственно из определения и условий инициализации переменной αt(j) для алгоритмов прямого-обратного хода и Витерби [1], который в последнее время выделяется практически как самостоятельный метод динамического программирования [4]. При этом объем требуемой памяти увеличивается примерно в D раз, а число необходимых вычислительных операций - примерно в ![]() раз по сравнению с обычными СММ.
раз по сравнению с обычными СММ.
Так, при количестве отсчетов времени T = 200 и числе состояний N = 7 для вычисления всех αt(j), где ![]() , алгоритм прямого-обратного хода потребует порядка
, алгоритм прямого-обратного хода потребует порядка ![]() операций.
операций.
Так, для значения D порядка 25 (что приемлемо для многих задач, связанных с обработкой речи) объем вычислений увеличивается примерно в 300 раз:
![]() операций
операций
Однако это по-прежнему меньше, чем при использовании прямых вычислений [1], требующих
![]() операций.
операций.
Другая проблема, связанная с моделями этого типа, состоит в том, что помимо обычных параметров СММ для них необходимо оценивать также большое (равное D) число новых параметров, связанных с каждым состоянием. Кроме того, при фиксированном числе наблюдений T обучающее множество с явно заданной плотностью длительности состояний содержит, в среднем, меньше переходов между состояниями и, следовательно, меньше данных для оценивания величин ρi(d), чем это было бы в случае стандартной СММ.
Но в тоже время функция плотности длительности состояний позволяет модифицировать алгоритм Витерби, максимизируя не предыдущее состояние, а длительность текущего.
Заключение. Таким образом, можно сформулировать следующие преимущества и недостатки использования и управления функцией плотности длительности состояний скрытых марковских моделей. Среди преимуществ стоит выделить:
(1) Значительно улучшается качество моделирования, а, значит, и качество распознавания.
(2) Возможность использования для модификации алгоритма Витерби, позволяющего:
(а) существенно быстрее восстанавливать порядок состояний модели благодаря уже имеющейся информации о длительности каждого состояния;
(b) автоматически разрешать равновероятностные переходы.
Среди недостатков отметим:
(1) Значительный рост вычислений, обусловленный введением изменяющихся длительностей состояний.
(2) Увеличение объема требуемой памяти.
(3) Необходимость оценивать большое число новых параметров, связанных с каждым состоянием (примерно равное D).
Нетрудно видеть, что некоторые преимущества и недостатки почти противоречат друг другу. Данная ситуация легко объясняется тем, что рост вычислений приходится более короткий промежуток времени, что в итоге должно дать преимущество в точности и, вероятно, скорости распознавания.
Данная работа была выполнена автором в качестве дополнительной проверки рациональности реализации разработанного модифицированного алгоритма Витерби.
Работа выполнена при поддержке гранта Правительства Петербурга № 3.11/04-06/50.
Список литературы
- Рабинер Л.Р., Шафер Р.В. Цифровая обработка речевых сигналов: пер. с англ.; под. ред. М.В. Назарова и Ю.Н. Прохорова. - М.: Радио и связь, 1981. - 496 с.
- Иконин С.Ю., Сарана Д.В. Система автоматического распознавания речи SPIRIT ASR Engine // Цифровая обработка сигналов. - 2003. № 4.
- Гультяева Т.А. Скрытые Марковские процессы. - Новосибирск: Изд-во НГТУ.
- Аграновский А.В., Леднов В.А. Теоретические аспекты обработки и классификации речевых сигналов. - М.: Радио и связь, 2004. - 164 с.
- Tebelskis J. Speech Recognition using Neural Networks. School of Computer Science Carnegie Mellon University. - 1995. - 190 p.
- Rabiner L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition // IEEE. - 1989. - Vol. 77, №2. - С. 257-286.
Библиографическая ссылка
Балакшин П.В. ФУНКЦИЯ ПЛОТНОСТИ ДЛИТЕЛЬНОСТИ СОСТОЯНИЙ СММ. ПРЕИМУЩЕСТВА И НЕДОСТАТКИ // Современные проблемы науки и образования. – 2011. – № 1. ;URL: https://science-education.ru/ru/article/view?id=4574 (дата обращения: 23.04.2024).



