Основными проблемами школьного образования в настоящее время являются немотивированность учебно-познавательной деятельности учащихся, их слабое стремление к познанию, отсутствие познавательного интереса и др. Сейчас идет активный поиск выходов из создавшегося положения.
Образовательная теория и школьная практика показывают, что многие проблемы могут быть решены не столько за счет корректировки содержания обучения, сколько за счет использования активных методов обучения, таких как метод проектов, мозговой штурм, кейс-метод и т. д.
Анализ школьной практики и передовых технологий обучения показывает, что значимой является организация учебно-исследовательской работы учащихся, в ходе которой школьники овладевают навыками и способами умственной деятельности, систематической самостоятельной поисковой деятельности.
Учебно-исследовательская деятельность учащихся по математике выполняет как обучающую, так и развивающую функцию, и это есть результат того, что настоящая деятельность воспитывает у обучающихся осознанное отношение к своему труду, формирует качество творческой деятельности и напрямую связана с развитием познавательного интереса как к различным видам математической деятельности, так и к различным аспектам содержания математики.
По организации учебно-исследовательской деятельности учащихся по математике читатель найдет материал в работах [1–3].
Подходящей темой для организации учебно-исследовательской работы учащихся является тема «Конические сечения». В данной статье мы ставим задачу провести исторический экскурс в развитие темы «Конические сечения» (этот материал может быть использован на вводном занятии математического кружка, посвященном изучению кривых второго порядка), а также предложить ряд задач по теории конических сечений, которые могут послужить материалом для проведения учебно-исследовательской работы (предложены задачи, в которых объектом исследования является эллипс).
Материалы и методы исследования
Ученые-математики Древней Греции активно занимались исследованиями задач, которые впоследствии стали называться знаменитыми задачами древности: об удвоении куба, о трисекции угла, о квадратуре круга. Работа с ними вывела ученых на проблему, связанную с изучением линий, отличных от прямых и окружностей: эллипс, парабола, гипербола.
Менехм (IV в. до н.э.) предложил для решения этих задач конические сечения – это такие кривые, которые получаются сечением конуса плоскостью, перпендикулярной одной из образующих (получаются три различные кривые в зависимости от того, какой конус сечется плоскостью – остроугольный, прямоугольный или тупоугольный). Позднее Аполлоний (III в. до н.э.) назвал их эллипсом, параболой, гиперболой. Он проводил сечения в произвольном конусе плоскостью под любым углом к оси конуса.
Основателем современного учения о кривых по праву считают великого немецкого художника и ученого А. Дюрера (1471–1528 гг.). В его сочинениях изложены основания геометрии и теории перспективы; подробно рассмотрено учение о правильных многогранниках; предложены решения знаменитых задач древности (скорее всего следует сказать – показана невозможность их решения с помощью циркуля и линейки); дана теория кривых линий.
Одно сечение конуса плоскостью называется эллипсом (эта фигура получается в тех случаях, когда секущая плоскость расположена под разными углами к оси конуса). На рисунке 1 приведено такое сечение.
Ссылаясь на книгу Эрика Т. Белла «Математика – царица и служанка наук», можно отметить, что круг и окружность нас привлекают с первого взгляда своей простотой, но при пристальном изучении различных кривых можно прийти к выводу, что идеальная пустота круга и окружности уступает тем сведениям, которые щедро дарит эллипс.
Среди древних греков, изучавших кривые второго порядка, были Менехм и Аполлоний Пергский. Их исследования показали, что после окружности эллипс является простейшей фигурой. Ученые прилагали усилия, дабы дать эллипсу определения: одни шли путем составления соответствующей формулы, задающей эллипс, другие же за основу определения брали существенное свойство эллипса.
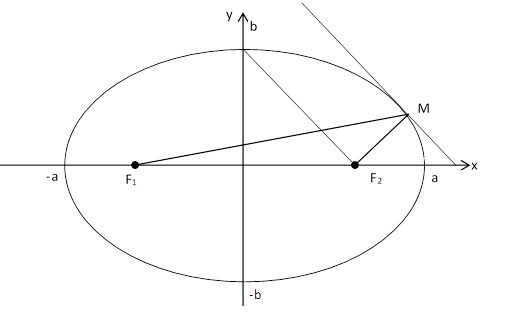
Рис. 1. Эллипс
На рисунке 1 показан способ построения эллипса, основанный на его главном свойстве: расстояние от точек эллипса до его двух фокусов есть величина постоянная.
На рисунке 2 показан способ построения эллипса с помощью двух кнопок, на которые надета петля из нитки; двигая карандаш вокруг кнопок, натянув при этом нитку, можно изобразить эллипс.
В реальной жизни мы увидим эллипс в том случае, если стакан с водой наклонить, в результате чего поверхность воды примет форму эллипса [4, 5].
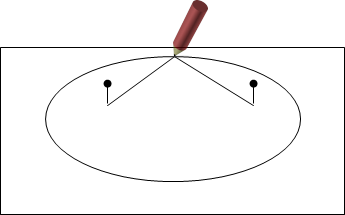
Рис. 2. Построение эллипса с помощью нитки и карандаша
У эллипса есть замечательное оптическое свойство [6]: если из одного фокуса эллипса направить луч света, то он, отражаясь от эллипса, попадет в другой его фокус.
Если вращать эллипс вокруг прямой, проходящей через его фокусы, то получим эллипсоид. Если покрыть его изнутри зеркальным слоем, то эта зеркальная поверхность обладает интересными свойствами:
1) если точечный источник света поместить в одном из фокусов эллипсоида, то лучи, отразившись от стенок эллипсоида, пройдут через его второй фокус;
2) если в одном из фокусов эллипсоида поместить точечный источник света и произвести «мгновенную» вспышку, то через некоторое время после многократных отражений от идеальной зеркальной поверхности эллипсоида все лучи практически сконцентрируются вдоль его большой оси [7, 8].
Результаты исследования и их обсуждение
Существуют способы построения точек эллипса с помощью циркуля и линейки. Например, в справочнике [4] на страницах 60, 61 описаны два способа. Еще один способ – авторский – предлагается в данной статье. Решается следующая задача.
Задача 1. На плоскости заданы точка О и два отрезка с длинами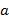 
, b; 
> b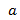. Построить точки эллипса с этими полуосями и центром О.
Для решения проведем через точку О две взаимно перпендикулярные прямые, одну из них назовем горизонтальной, другую – вертикальной. На ней отложим отрезок OB = b вверх, вниз отложим отрезок OB1 = 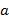– b. Берем произвольно точку N между O и B1, построим окружность с центром в этой точке радиуса 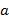– b. Она пересекает горизонталь в двух точках; выберем ту из них, которая лежит правее O. Обозначим ее через M. Проведем прямую NM. Опишем окружность с центром M радиуса «b». Она пересекает прямую в двух точках. Пусть P – та из них, которая лежит «северо-восточнее». Это и будет искомая точка эллипса.
Меняя N, получим новые точки эллипса.
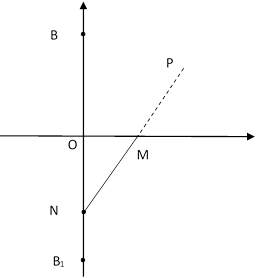
Рисунок 3а поясняет описанное построение. Рисунок 3б служит для его обоснования, приводимого ниже.
Пусть t – параметр, меняющийся на отрезке [0, –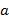
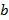] и служащий для задания координат точек N, M, P. Положим N (0; –t), тогда M(
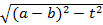; 0).
Запишем уравнение прямой NM в виде
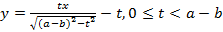(1)
и уравнение окружности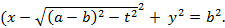 
Для нахождения точки P объединим эти уравнения в систему и решим ее.
Систему сведем к квадратному уравнению:
.
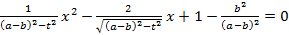Опуская детали, укажем его корни:
.
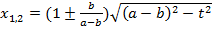а) 
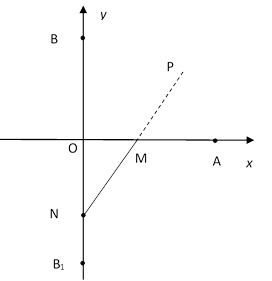б)
Рис. 3. Построение точек эллипса
Так как абсцисса точки P должна быть больше абсциссы точки M, то подходит только первый корень:
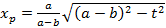. (2)
Тогда из равенства (1) имеем:
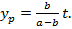(3)
Нетрудно проверить, что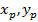 
удовлетворяют уравнению эллипса:
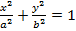, так что точка P ему принадлежит при любом
.
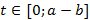Заметим, что при t=0 точка P совпадает с правой вершиной A (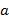, 0) эллипса, а при t=
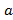– b она переходит в верхнюю границу B (0, b). Таким образом, по формулам (2) и (3) получено параметрическое задание дуги AB эллипса. Расставляя в этих формулах в правых частях нужные знаки, получим параметрические задания остальных дуг.
Правые части равенств (2), (3) можно переписать соответственно в виде:
, 
.
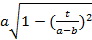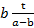Здесь дробь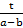 
заключена между 0 и 1, поэтому она является синусом некоторого угла 
.
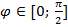Тогда равенства (2), (3) запишутся в виде:
Получим известное параметрическое задание эллипса.
В заключение предлагаем читателям, любителям алгебры, решить следующую задачу.
Запишите систему уравнений, в которой первое уравнение – это уравнение окружности с центром M, радиуса «b», второе уравнение – уравнение эллипса. Докажите, что одним из решений системы является пара (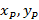
).
Задача 2. Требуется ответить на проблемный вопрос: «Можно ли эллипс, площадь которого равна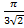
, вписать в квадрат, сторона которого равна 1?
Решение. Контекст задачи подсказывает, что мы должны найти полуоси a и b того эллипса, который мы хотим вписать (положим полуось a > полуоси b). Не будем рассматривать случаи, когда a = 
и b =
.
В основу решения этой задачи положим координатный метод, для чего введем систему координат, такую, какая показана на рисунке 4 (сторона СD квадрата касается дуги эллипса AB в точке K, и это касание происходит в первой четверти плоскости).
Координаты точки касания K мы найдем, решив систему:
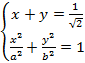, (4)
Выразив из первого уравнения переменную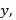 
мы получим квадратное уравнение:
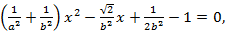
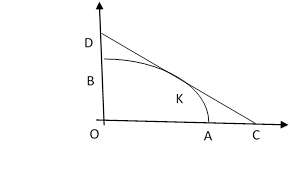
Рис. 4. Рисунок к задаче 2
или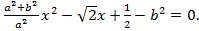 
(5)
Раз мы имеем одну точку касания в первой четверти плоскости, то понятно, что это квадратное уравнение должно иметь один корень, а как известно, это возможно в случае, когда его дискриминант равен нулю.
Дискриминант этого уравнения:
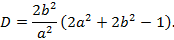
Из этого следует, что:
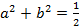. (6)
При нулевом дискриминанте корнем уравнения (5) является
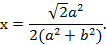
Найдена абсцисса точки касания, равная согласно (5)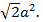 
Ее ордината 
= 
.
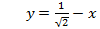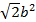При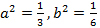 
площадь эллипса:
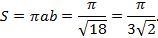
На поставленный в задаче 1 вопрос можно ответить утвердительно.
Введем понятие «прямоугольник, охватывающий эллипс»: если у эллипса полуоси a и b, то такой эллипс оказывается вписанным в прямоугольник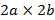 
, и такой прямоугольник мы и назовем охватывающим. Два прямоугольника подобны, если отношения их сходственных сторон равны:
.
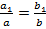Задача 3. С помощью циркуля и линейки в заданный эллипс, полуоси которого a и b, вписать прямоугольник, подобный прямоугольнику, охватывающему эллипс.
Решение. У прямоугольника, охватывающего эллипс, проведем диагонали и обозначим точки пересечения этих диагоналей с эллипсом. Этот эллипс и окажется искомым.
Аргументируем построение такого эллипса. На рисунке 5 изображена система координат, в которой построен квадрат, а в него вписан эллипс. Проведены диагонали квадрата, вертикальная и горизонтальная оси симметрии.
Рассмотрим диагональ, идущую на «северо-восток». Решим систему
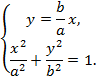
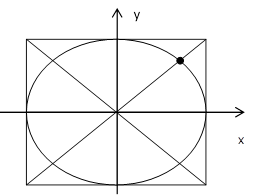
Рис. 5. Рисунок к задаче 3
Одно из решений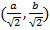 
задает точку в первой четверти плоскости (на рисунке 5 она отмечена). Мы показали построение лишь одной вершины прямоугольника, а читателю предлагаем осуществить построение и узнать координаты трех других вершин прямоугольника.
В построенной задаче 3 в прямоугольник впишем эллипс, который назовем «подобный охватывающему». Эти построения мы продолжим дальше. При этом у всех эллипсов удалим внутренние точки. Получим плоскую фигуру – своеобразный «ковер».
Задача 4. Какова площадь такого «ковра»?
Решение. Обозначим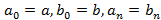
– полуоси эллипса на n-ом шаге процесса.
Согласно задаче 3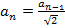 
, 
; 
.
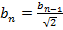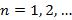Площадь «ковра» получается, если из суммы площадей всех прямоугольников вычесть сумму всех эллипсов:
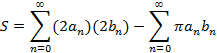
Так как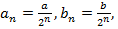 
то по формуле суммы всех членов убывающей геометрической прогрессии со знаменателем имеем:
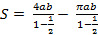= 2ab(4 –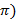 
Введем обозначение D = 4 –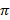 
.
Площадь полученного «ковра»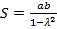 
D. (7)
Задача 5. Доказать следующее оптимальное свойство эллипса: лучи света, исходящие из одного фокуса F1, после зеркального отражения от эллипса проходят через второй фокус F2 [8].
Решение читатель может найти в учебнике [9] на страницах 167–168 и в наших работах [7, 8].
Заключение
Как показывает практика, предложенные задачи вызывают у учащихся математических классов интерес, их решение формирует у них умения исследовательского характера.
Материал по данной теме читатель найдет в наших работах [10, 11], в статьях журнала «Математика в школе» [12–14] и в работах Е.В. Потоскуева [15, 16].
Библиографическая ссылка
Далингер В.А. УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА УЧАЩИХСЯ МАТЕМАТИЧЕСКИХ КЛАССОВ, СВЯЗАННАЯ С РЕШЕНИЕМ НЕКОТОРЫХ ЗАДАЧ ПО ТЕОРИИ КОНИЧЕСКИХ СЕЧЕНИЙ // Современные проблемы науки и образования. – 2020. – № 2. ;URL: https://science-education.ru/ru/article/view?id=29660 (дата обращения: 25.04.2024).