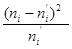В процессе математической подготовки студентов в метрическом компетентностном формате как в одной из форм педагогической технологии необходимо установить достаточно точные метрики средств обучения, в частности продолжительность тестового контроля знаний, оценку сложности тестовых задач.
Цель исследования. Педагогическое тестирование как инструмент проверки качества усвоенных знаний является широко распространенным средством контроля знаний студентов. К примеру, методика оценки продолжительности тестирования для дисциплины «Прикладная математика» направления подготовки «Информационные системы и технологии» рассмотрена в [1]. Какова продолжительность тестирования при изучении курса высшей математики студентами направления «Химическая технология» в технологическом университете, чтобы объективно, т.е. с учетом психологических и интеллектуальных особенностей обучаемого, оценить качество усвоенных им знаний?
Материал и методы исследования. Пусть S – продолжительность временного интервала, в течение которого преподаватель (эксперт) выполнит все задания предложенного теста (S – экспертное время). Очевидно, что ни один из студентов не выполнит тестовые задания за время, меньшее S. Обозначим через V время окончания студентами всего теста, т.е. весь состав тестируемых студентов закончит работу на интервале [S;V].
Тест на полноту усвоенных знаний содержит 10 вопросов (полнота знаний – это мера знаний теории в рамках рассматриваемой дисциплины). Варианты теста являются однородными по содержанию и одинаковыми по сложности. Сложность каждого задания случайно выбранного теста оценивает эксперт – преподаватель в минутах работы (мин/раб) [2].
Перейдем к оценке случайной величины Х – времени выполнения студентом теста на полноту усвоенных знаний. Ее значение лежит в достаточно широком диапазоне: скорость реакции студентов на вопрос теста различна [3]. Нужно учесть и тот факт, что некоторые студенты не успевают ответить на вопрос по причине незнания материала. Таким студентам время тестирования можно увеличивать сколь угодно, но качество ответов от этого не улучшится [4].
К промежуточному экзамену (коллоквиуму) по теме «Дифференциальное исчисление функции одной переменной» были допущены 115 студентов. Усредненные данные представлены в таблице 1.
Таблица 1
Закон распределения случайной величины X теста на полноту усвоенных знаний
|
№ |
Срединное значение интервала, S |
Значение эмпирической функции распределения |
|
1 |
1,125 |
0 |
|
2 |
1,375 |
0,017 |
|
3 |
1,625 |
0,077 |
|
4 |
1,875 |
0,155 |
|
5 |
2,125 |
0,285 |
|
6 |
2,375 |
0,459 |
|
7 |
2,625 |
0,659 |
|
8 |
2,875 |
0,859 |
|
9 |
3,125 |
0,937 |
|
10 |
3,375 |
0,981 |
|
11 |
3,625 |
0,998 |
Пусть Х – случайная величина – время выполнения студентом тестовых заданий. 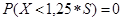 , т.е. вероятность того, что студент выполнит тестовые задания за время, меньшее, чем 1,25
, т.е. вероятность того, что студент выполнит тестовые задания за время, меньшее, чем 1,25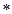 S, равна нулю, где S – сложность теста. Ко времени 2,75
S, равна нулю, где S – сложность теста. Ко времени 2,75 S тестирование завершит чуть более половины студентов:
S тестирование завершит чуть более половины студентов: 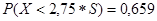 и т.д. Из данных таблицы видно, что время выхода студентов по завершении тестирования начинается с момента времени
и т.д. Из данных таблицы видно, что время выхода студентов по завершении тестирования начинается с момента времени 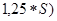 . В этом случае величина
. В этом случае величина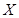 будет распределена по нормальному закону с распределением Гаусса [5]. Полигон относительных частот, представленный на рисунке 1, иллюстрирует тот факт, что студенты стараются как можно полнее использовать отведенный лимит времени и заканчивают тестирование по его истечении. Возникает вопрос: сколько времени (величина V) нужно дать студентам, чтобы они ответили на поставленные 10 вопросов независимо от скорости (быстроты) реакции при достаточной подготовке по конкретному разделу?
будет распределена по нормальному закону с распределением Гаусса [5]. Полигон относительных частот, представленный на рисунке 1, иллюстрирует тот факт, что студенты стараются как можно полнее использовать отведенный лимит времени и заканчивают тестирование по его истечении. Возникает вопрос: сколько времени (величина V) нужно дать студентам, чтобы они ответили на поставленные 10 вопросов независимо от скорости (быстроты) реакции при достаточной подготовке по конкретному разделу?
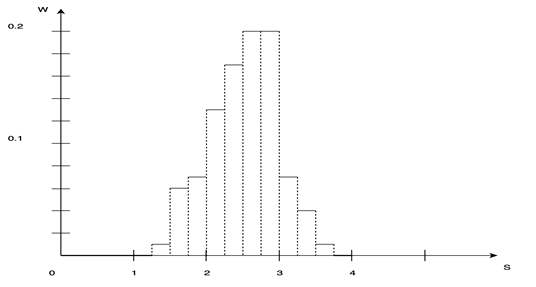
Рис. 1. Полигон относительных частот времени тестирования
Тест на полноту содержит вопросы теоретического характера: определения, свойства, методы вычисления соответствующих характеристик, приложения. Соответственно, независимо от продолжительности тестирования V оценка за тест, как правило, полностью зависит от степени подготовленности студента. Понятно, что многие студенты, даже выполнив все задания, не покидают аудиторию до окончания тестирования (параметр V). Однако неподготовленным студентам выделенного для ответов времени всегда будет недостаточно. Цель данной работы – обосновать выбор времени V, так как излишнее увеличение времени тестирования не приведет к улучшению качества ответов студентов.
Авторами выполнен значительный объем наблюдений при проведении тестирования со студентами института нефти и нефтехимии по следующим разделам курса высшей математики: линейная и векторная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисления функции одной переменной, комплексные числа, дифференциальные уравнения. Полученные результаты дают основание считать, что продолжительность тестирования не должна превышать величины 3S, а функция плотности вероятности распределения времени тестирования имеет вид, представленный на рисунке 2 (V = 3S).
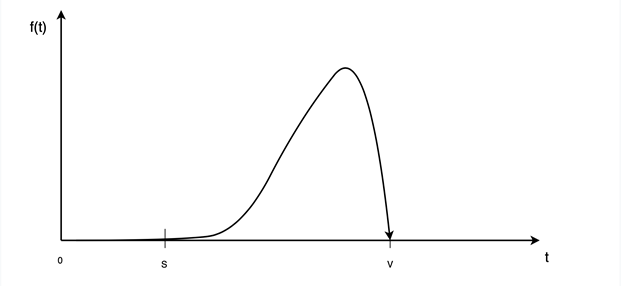
Рис. 2. Вид функции плотности вероятности случайной величины Х
В таблице 2 представлен статистический ряд данных на полноту усвоенных знаний по линейной, векторной алгебре (объем выборки n = 77).
Таблица 2
Наблюдаемые частоты, полученные в ходе тестирования
|
Номер интервала |
Интервал, S |
Частота ni |
|
1 |
[1; 1,25) |
2 |
|
2 |
[1,25;1,5) |
2 |
|
3 |
[1,5; 1,75) |
8 |
|
4 |
[1,75; 2) |
8 |
|
5 |
[2; 2,25) |
9 |
|
6 |
[2,25; 2,5) |
11 |
|
7 |
[2,5; 2,75) |
16 |
|
8 |
[2,75; 3) |
17 |
|
9 |
[3; 3,25) |
4 |
Описание зависимости, представленной на рисунке 2 и соответственно в таблице 2, достаточно сложно, поэтому предлагается другой путь, более простой в реализации и интерпретации результатов. А именно вводится линейная функция вида:
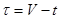 ,
,
представляющая собой преобразование координат. При этом начало координат переносится в точку 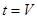 , ось абсцисс меняет свое направление на противоположное, а величина
, ось абсцисс меняет свое направление на противоположное, а величина 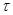 , имея смысл обратного времени, показывает, сколько времени осталось до конца тестирования. Точка S оси t отображается на оси
, имея смысл обратного времени, показывает, сколько времени осталось до конца тестирования. Точка S оси t отображается на оси 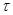 в точку V – S. Полигон относительных частот «обратного времени» представлен на рисунке 3, вариационный ряд – в таблице 3.
в точку V – S. Полигон относительных частот «обратного времени» представлен на рисунке 3, вариационный ряд – в таблице 3.
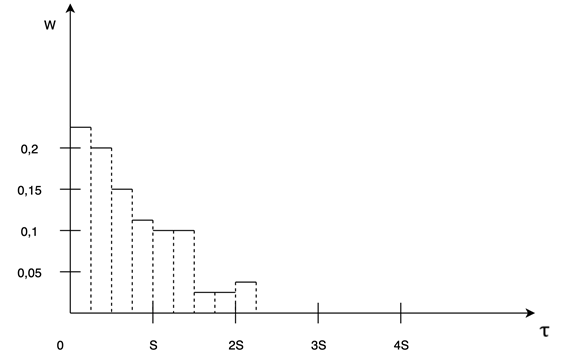
Рис. 3. Полигон относительных частот «обратного времени»
Таблица 3
Вариационный ряд «обратного времени»
|
Номер интервала
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Интервал «обратное время», |
(0;0,25] |
(0,25;0,5] |
(0,5;0,75] |
(0,75;1] |
(1;1,25] |
(1,25;1,5] |
(1,5;1,75] |
(1,75;2] |
> 2 |
|
Частота ni |
17 |
16 |
11 |
9 |
8 |
8 |
2 |
2 |
4 |
Функция плотности вероятности распределения «обратного времени» 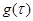 с достаточной степенью точности аппроксимируется кривой, приведенной на рисунке 4, описание которой задается однопараметрической функцией:
с достаточной степенью точности аппроксимируется кривой, приведенной на рисунке 4, описание которой задается однопараметрической функцией:
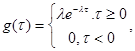
где 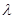 интерпретируется как интенсивность выхода студентов по окончании выполнения
интерпретируется как интенсивность выхода студентов по окончании выполнения
тестовых заданий и определяется как величина, обратная среднему времени тестирования, т.е. 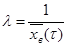 .
.
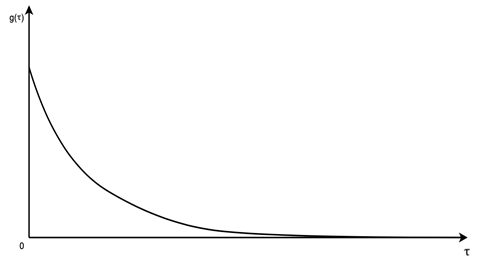
Рис. 4. Вид функции плотности вероятности распределения «обратного времени»
Определение экспертного времени S не вызывает затруднений и является, как правило, достаточно надежной величиной. Значение интенсивности 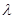 как величины, обратной среднему времени тестирования, не обладает подобной устойчивостью, поскольку степень готовности студентов к тестированию различна. Проверим гипотезу о том, что время, оставшееся до конца тестирования, при уровне значимости 0,05 распределено по показательному закону, т.е. функция
как величины, обратной среднему времени тестирования, не обладает подобной устойчивостью, поскольку степень готовности студентов к тестированию различна. Проверим гипотезу о том, что время, оставшееся до конца тестирования, при уровне значимости 0,05 распределено по показательному закону, т.е. функция 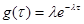 может быть использована для описания данной величины (случайная величина
может быть использована для описания данной величины (случайная величина 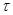 – «обратное время»). Проверку выполним по классическому критерию согласия
– «обратное время»). Проверку выполним по классическому критерию согласия 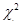 . Результаты вычислений сведены в таблицу 4.
. Результаты вычислений сведены в таблицу 4.
Таблица 4
Наблюдаемые и теоретические частоты, полученные в ходе эксперимента
|
Номер интервала |
ni |
ni ‘ |
|
|
1 |
17 |
21,637 |
0,994 |
|
2 |
16 |
15,554 |
0,013 |
|
3 |
11 |
11,165 |
0,002 |
|
4 |
9 |
8,085 |
0,104 |
|
5 |
8 |
5,775 |
0,857 |
|
6 |
8 |
4,235 |
3,308 |
|
7 |
2 |
2,926 |
0,293 |
|
8 |
2 |
2,233 |
0,024 |
|
9 |
4 |
5,39 |
0,358 |
|
|
n = 77 |
ni ‘= 77 |
|
Теоретические значения частот 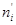 вычислялись по формуле
вычислялись по формуле 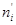 =
= 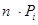 , где n – объем
, где n – объем
выборки, 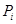 – относительная частота соответствующего разряда экспоненциальной функции
– относительная частота соответствующего разряда экспоненциальной функции
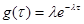 ; для нахождения выборочной средней
; для нахождения выборочной средней 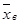 в качестве «представителя» i-го интервала принималась его середина
в качестве «представителя» i-го интервала принималась его середина 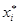 =
= 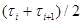 :
:
– выборочная средняя, где 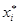 – середина интервалов таблицы 3:
– середина интервалов таблицы 3:
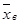 = (17
= (17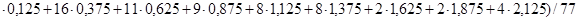 = 0,76;
= 0,76;
–- оценка параметра предполагаемого показательного распределения:
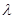 = 1 /
= 1 / 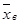 = 1 / 0,76 = 1,32.
= 1 / 0,76 = 1,32.
Таким образом, дифференциальная функция предполагаемого показательного распределения имеет вид 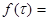 1,32
1,32 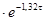 (
(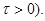 ;
;
– вероятности попадания 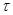 в каждый из интервалов:
в каждый из интервалов: 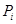 =
= 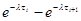 . Например, для первого интервала
. Например, для первого интервала 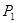 =
= 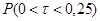 =
= 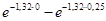 = 1 – 0,719 = 0,281. Аналогично вычисляются вероятности в остальных интервалах: Р2 = 0,202, Р3 = 0,145, Р4 = 0,105, P5 = 0,075,
= 1 – 0,719 = 0,281. Аналогично вычисляются вероятности в остальных интервалах: Р2 = 0,202, Р3 = 0,145, Р4 = 0,105, P5 = 0,075,
Р6 = 0,055, Р7 = 0,038, Р8 = 0,029, Р9 = 0,07;
– теоретические частоты 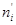 =
= 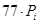 ,
, 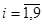 :
: 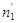 = 21,637,
= 21,637, 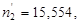
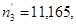
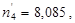
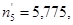
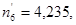
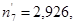
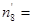 2,233,
2,233, 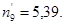 ;
;
– определяем значение критерия 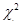 по формуле :
по формуле :
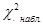 =
= 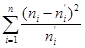 =5,953;
=5,953;
– по таблице критических точек распределения 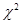 , по заданному значению
, по заданному значению 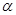 =0,05 и числу степеней свободы
=0,05 и числу степеней свободы 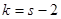 = 9 – 2 =7 находим
= 9 – 2 =7 находим 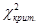 =
= 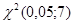 = 14,1.
= 14,1.
Так как 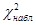 <
< 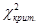 , то нет оснований отвергнуть гипотезу о показательном распределении «обратного времени».
, то нет оснований отвергнуть гипотезу о показательном распределении «обратного времени».
Результаты исследования, выводы. Итак, при подготовке к тестированию студентов исходя из полученных результатов необходимо действовать по следующему алгоритму:
– эксперт (преподаватель) оценивает S – сложность (трудоемкость в мин/раб) теста;
– продолжительность теста V полагается равной 3S: V = 3S.
Как показывает опыт, полученную эвристическую формулу V = 3S (обоснованная продолжительность тестирования) можно использовать только в ограниченном диапазоне измерений S. При S > 25 мин результат тестирования ухудшается: начинает действовать новый фактор – усталость студента. В нашем случае S = 8 мин.
Библиографическая ссылка
Хузиахметова А.Р., Нуриев Н.К., Хузиахметова Р.Н. ОЦЕНКА ПРОДОЛЖИТЕЛЬНОСТИ ТЕСТИРОВАНИЯ В ЗАВИСИМОСТИ ОТ СЛОЖНОСТИ ТЕСТА // Современные проблемы науки и образования. – 2019. – № 3. ;URL: https://science-education.ru/ru/article/view?id=28818 (дата обращения: 26.04.2024).




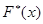
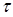 (S)
(S)