В настоящее время система образования претерпевает значительные изменения. Происходит переход к новой парадигме «выпускника школы, подготовленного к жизнедеятельности», положенной в основу ФГОС школы второго поколения, которые в первую очередь ориентированы на реализацию развивающего потенциала. Одной из задач обучения математике является формирование мышления школьников, готовности действовать в ситуации выбора, необходимости анализа альтернативных позиций. Сегодня перед учителем математики стоит не только задача формирования приемов логического мышления, но и дивергентного (предполагающего многовариантность исходов рассуждений). Решение стандартных математических задач не позволяет достичь поставленные временем цели. В качестве средства в данной статье рассмотрим задачи с недостающими или избыточными данными, которые получили название «некорректные задачи». Как показывает практика, такие задачи редко встречаются в школьных учебниках, и обучающиеся испытывают затруднения при работе с ними.
Вопросами работы с такими задачами занимались В.А. Крутецкий [1], Н.В. Метельский [2], А.Ф. Эсаулов [3] и др. В имеющихся исследованиях в основном представлены виды некорректных задач и их влияние на развитие мыслительных процессов. М.А. Холодная, Э.Г. Гельфман [4] берут более широкое понятие – «развивающие учебные тексты», в состав которых включают и задачи, направленные на формирование готовности работать с противоречивой информацией, невозможной ситуацией, выбора способа деятельности. Ряд ученых изучали способы применения некорректных задач в математике (Т.А. Безусова [5], Э.Г. Гельфман [4], И.Г. Просвирова [6], З.П. Матушкина [6] и др.). Н.В. Аммосова, Б.Б. Коваленко [7] приводят примеры геометрических задач 8-9 классов с избыточным (недостаточным) набором данных и описывают приемы работы с ними. Рассматривая общие подходы работы с геометрической задачей, Л.П. Шебанова [8] вставляет задания на отыскание ошибок (противоречий) в тексте, чертеже, решении. В качестве основного метода развития компетенций обучающихся основной школы V. Utemov, A. Masalimova [9] предлагают рассматривать прием моделирования и адаптации творческих математических задач с учетом их уровней сложности. Авторы предлагают рассматривать «шесть требований к условиям задачи, выявленных в ходе экспериментального обучения: противоречие в условии задачи, достаточность условия, правильность вопроса, независимость фактов, полнота информации, научная состоятельность» [9, с. 4360]. In’am A. [10] изучает влияние уровня развития логического мышления на умение решать геометрические задачи (акцент делается на последовательность и обоснованность решения).
Целью нашего исследования являлось выделение условий формирования у обучающихся умения работать с некорректными задачами. Гипотезой исследования выступало предположение о том, что процесс формирования умения работать с некорректными задачами у школьников будет эффективным, если выполняются следующие условия. Во-первых, вместе с традиционными геометрическими задачами используются некорректные задачи, а также задачи, которые на них похожи. Во-вторых, в процесс обучения включаются задания на преобразование избыточной противоречивой задачи через исключение лишних данных или изменение вопроса задачи; на дополнение условия некорректной задачи. В-третьих, предлагаются обучающимся задания на составление задач по готовым чертежам (схемам, уравнениям, формулам), их дополнение необходимыми данными. Достижения поставленной цели обусловлено решением следующих задач: выделить действия, входящие в состав умения работать с некорректной задачей; выявить содержательные компоненты для работы с некорректными задачами; провести опытно-экспериментальную работу по повышению уровней сформированности рассматриваемого умения.
Материалы и методы исследования. В качестве методов исследования выступили: обобщение и анализ педагогического опыта, описанного в психолого-педагогической и методической литературе; опытно-экспериментальная работа; статистическая обработка количественных данных об уровнях сформированности умения работать с некорректной задачей.
Опытно-экспериментальная проверка эффективности представленных в гипотезе условий формирования у школьников действий, входящих в состав умения работать с некорректной задачей, проводилась в 2017-2018 учебном году на уроках по геометрии в 10 классе. В ней принимали участие 22 человека экспериментальной группы и 19 человек контрольной группы, давших свое согласие на проведение исследования. Для диагностики были составлены наборы некорректных задач различных степеней сложности, соответственно действиям, входящим в состав умения работать с некорректной задачей.
Работа состояла из трех этапов: констатирующего среза, формирующего этапа и контрольного среза.
На первом и третьем этапах школьникам предлагалось выполнить 6 заданий, проверяющих сформированность действий, входящих в состав умения работать с некорректной задачей (на каждое действие по 1 задаче). Примеры заданий представлены в таблице 1. Действия, входящие в состав умения работать с некорректной задачей, были выделены следующие:
1 - определять недостающую информацию в тексте задачи;
2 - видеть альтернативность условия задачи;
3 - искать необходимую информацию для решения задачи из различных источников;
4 - доопределять условие задачи данными, которые имеются в задаче «между строк»;
5 - организовывать найденные данные (составление модели задачи);
6 - выявлять противоречие (обработка информации).
Таблица 1
Примеры заданий констатирующего среза
|
№ |
Действие |
Пример |
|
1 |
определять недостающую информацию в тексте задачи |
«В треугольнике АВС биссектриса АА1 продолжается за основание на отрезок А1Е и т. Е соединяется с т. С. Найдите ÐАСЕ, если ÐАСВ=47º, ÐВАС=62º». (Нет однозначного ответа) |
|
2 |
видеть альтернативность условия задачи |
«Дан четырехугольник с двумя парами равных сторон. Длины сторон четырехугольника 2 см и 2 |
|
3 |
искать необходимую информацию для решения задачи из различных источников |
«Найдите координаты вершин квадрата, если точка пересечения его диагоналей имеет координаты (7; -4), а одна из вершин лежит на оси Oy. Достаточно ли данных в задаче? При необходимости дополните условие, решите задачу» |
|
4 |
доопределять условие задачи данными, которые имеются в задаче «между строк» |
«В треугольнике АВС биссектриса АА1 продолжается за основание на отрезок А1Е и т. Е соединяется с т. С. Найдите ÐАСЕ, если ÐАСВ=47º, ÐВАС=62º». При необходимости дополните условие задачи, чтобы задача имела однозначный ответ (например, А1Е= АА1) |
|
5 |
организовывать найденные данные (составлять модель задачи, используя необходимые и достаточные данные) |
«Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках A1, B1, C1, D1. Найти длину отрезка DD1, если AA1=2 м, BB1=3 м, CC1=8 м, AA1: CC1= BB1: DD1». (Учащимся необходимо провести исследование, в процессе которого они выяснят, что условие задачи противоречиво и задача решения не имеет) |
|
6 |
выявлять противоречие, ориентироваться в избыточном количестве информации |
«Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная его плоскости. Расстояния от К до вершин прямоугольника В, С и D равны 3 м, 9 м и 7 м соответственно. Найдите сторону АК». (Задача имеет противоречивое условие) |
Каждое задание оценивалось по 3-балльной шкале, затем суммировалиcь полученные результаты и делались выводы об уровне сформированности умения работать с некорректными задачами: от 0 до 6 баллов включительно – низкий, от 7 до 13 включительно – средний, от 14 до 18 – высокий. На контрольном срезе предлагалось решить 6 заданий, аналогичных по типологии некорректных задач.
Второй этап экспериментального исследования включал формирующий эксперимент, который проводился по специально отобранным темам. Сущность эксперимента заключалась в изменении одних переменных (условий) реализации учебного процесса, но при этом другие условия были сохранены. К неизменным переменным (неварьируемым условиям) в нашем исследовании были отнесены информационные компоненты содержания учебного материала по геометрии, представленного в программе для 10 класса общеобразовательных учреждений. Варьируемые условия представлены комплексом некорректных задач, предлагаемых в процессе обучения геометрии.
Результаты исследования и их обсуждение. В начале работы был проведен констатирующий срез, результаты констатирующего среза представлены в таблице 2. Задания среза представлены в таблице 1. Срез проводился в контрольной и экспериментальной группах. Результаты среза показали, что классы по сформированности умения работать с некорректной задачей находятся примерно на одном уровне.
Таблица 2
Сопоставление экспериментальной и контрольной групп 10 класса по результатам констатирующего среза
|
Уровни умения работать с некорректной задачей |
Экспериментальная группа |
Контрольная группа |
||
|
количество обучающихся |
% |
количество обучающихся |
% |
|
|
Всего Высокий Средний Низкий |
22 0 19 3 |
100 0 86,4 13,6 |
19 2 13 4 |
100 10,5 68,4 21,1 |
Суть формирующего эксперимента состояла в том, что экспериментальным группам учащихся в начале обучения были заданы требования по организации занятий. Эксперимент был рассчитан на 42 учебных часа по следующим темам: «Параллельность прямых и плоскостей» (20 часов); «Перпендикулярность прямых и плоскостей» (22 часа). Уроки геометрии в 10-х классах ведутся на основе учебника А.В. Погорелова [11]. Содержание задачного материала учебника дополнялось некорректными задачами, а именно, те задачи, которые определены поурочным планированием, были переформулированы на основе приемов конструирования некорректных задач (замена данных условия более общими понятиями, дополнение условия следствиями из исходных данных, изменение требования задачи за счет его конкретизации и др.). Отметим, что на уроках использовались различные типы некорректных задач. Одновременно с ними ученикам предлагались и стандартные (корректные) задачи. Такая схема работы формировала у школьников установку внимательно анализировать текст задачи, проверять его на полноту и непротиворечивость. Описание содержательных компонентов и направлений работы с некорректными задачами различных типов приведено ниже.
Работа с задачами с недостающими данными велась через призму перечисленных ниже действий. Во-первых, выявление недостающих данных. Если недостающие данные удается доопределить (используя справочную литературу либо используя прием «между строк»), тогда данная задача будет решаться посредством применения различных случаев в соответствии с условиями задачи. Во-вторых, применение упрощенной модели задачи с достаточным для нее количеством имеющихся данных и решение полученной задачи. В-третьих, решение задачи, полагая недостающие данные известными. В данном случае решение выступает функцией от недостающих данных.
При решении задач с избыточными данными за основу берется любой набор данных, который приводит к необходимому решению (для различных способов решения наборы данных отличны). Для проверки полученного решения используются нерассмотренные данные, которые не были учтены в решении задач. При наличии противоречий могут получиться несколько вариантов решения (в отдельности с каждым из противоречивых данных). В конце необходимо проверить согласованность полученного решения с практическим наблюдением. Иногда допускается вариант, при котором отбрасывают оба противоречивых условия и решается задача с недостатком данных.
В контрольном классе была реализована традиционная методика обучения геометрии. В экспериментальной группе использовались некорректные задачи на всех этапах урока. Изменения предполагались в содержании задач, в формах и методах деятельности учащихся и педагога.
Логическая процедура внедрения экспериментального материала в экспериментальный класс заключалась в том, что на первых уроках по теме «Параллельность прямых и плоскостей» преобладали стандартные задачи, а на последующих уроках осуществлялся переход сначала к задачам с избыточными данными, при этом данные могли быть и противоречивыми. Приведем пример задачи: «Через концы отрезка AB длиной 4,8 м проведены параллельные прямые, пересекающие некоторую плоскость в точках C и D соответственно. Длина перпендикуляра, опущенного из точки C на прямую BD, равна 6,4 м. Найти длину перпендикуляра, опущенного из точки С на прямую AB, если прямая AB не пересекает плоскость и AC=7,2 м».
В ходе работы обучающиеся приходят к выводу, что задача не имеет решения, поскольку не существует параллелограмма, отвечающего условию задачи. Педагог ориентирует учеников на построение фигуры на основе данных задачи, что помогает более глубокому их анализу. Подобные задачи способствуют формированию умения рассматривать условие задачи как объект исследования.
С целью формирования у учащихся способности к критическому анализу информации им могут быть предложены задачи с противоречивыми данными, требования которых должны быть сформулированы не в форме «найдите», а в форме «существует ли». Приведем пример задачи: «Существует ли прямоугольник ABCD, стороны которого параллельны соответственно сторонам четырехугольника A1B1C1D1?». Подобные задачи составляются путем переформулировки (без учета естественных ограничений).
После того как отработан процесс исследования противоречивости условия задачи, можно переходить к подобным задачам на вычисление. В данном случае ученики проводят конструктивное исследование, в результате они должны прийти к заключению, что условие задачи противоречиво, а, значит, она не имеет решения. При этом педагог нацеливает учащихся на выяснение причин противоречия, установив которое, они обнаруживают, что задача переполнена, и после чего корректно составляют текст задачи. Перед обучающимся встает необходимость исключить избыточные данные. Для этого они переходят к задаче с недостающими данными и составляют на ее основе несколько новых задач, добавляя по одному из условий. Учащимся дается задание провести исследование с целью определения верно ли составлены задачи. В процессе работы приходим к заключению, что у этих задач имеется единственное решение. Исследовать условия сконструированных задач ученики могут с помощью построения фигур по тексту.
Далее школьникам предлагается решить задачу с недостающими данными. Пример задачи: «Концы данного отрезка, не пересекающего плоскость, удалены от нее на 0,3 м и 0,5 м. Как удалена от плоскости точка, делящая данный отрезок в отношении 3:7». Приведенная задача будет иметь два решения. Чтобы ученики смогли заметить альтернативность условия, достаточно провести построение.
На протяжении изучения курса геометрии для 10 класса в экспериментальном классе использовались задания на составление задач по уравнениям, рисункам, схемам. Предварительно предлагаемые модели анализировались, и при необходимости проводилось дополнение недостающими данными, или исправлялись ошибки и неточности.
В конце работы был проведен в контрольном и экспериментальном классе контрольный срез (задания среза по типологии были аналогичны заданиям, представленным в таблице 1, но немного сложнее). Результаты представлены в таблице 3.
Сопоставление результатов обучающихся в контрольной и экспериментальной группах подтверждает эффективность проведенной работы. Полученные результаты позволяют сделать вывод о том, что процесс формирования умения работать с некорректными задачами у школьников будет эффективным, если выполняются следующие условия, представленные в гипотезе исследования.
Таблица 3
Сопоставление экспериментальной и контрольной групп 10 класса по результатам контрольного среза
|
Уровни умения работать с некорректной задачей |
Экспериментальная группа |
Контрольная группа |
||
|
количество обучающихся |
% |
количество обучающихся |
% |
|
|
Всего Высокий Средний Низкий |
22 10 11 1 |
100 45,5 50 4,5 |
19 3 9 7 |
100 11,1 50 38,9 |
Результаты исследования могут быть использованы педагогами-исследователями для разработки научных обоснований и методических рекомендаций по вопросам формирования умения работать с некорректными задачами не только для школьников, но и студентов вузов, а также педагогами-практиками в образовательном процессе.
В целом можно говорить о положительной тенденции формирования у обучающихся школы рассмотренного умения с помощью выделенного содержания и видов работы. В процессе опытно-экспериментальной работы было выявлено, что описанные материалы и виды работы являются эффективными.
Заключение. В исследовании были поставлены задачи: выделить действия, входящие в состав умения работать с некорректной задачей; выявить содержательные компоненты для работы с некорректными задачами, которые целесообразно использовать для формирования этого умения; провести опытно-экспериментальную работу.
В результате проделанной работы выделены действия, входящие в состав умения работать с некорректной задачей: определять недостающую информацию в тексте задачи, видеть альтернативность условия задачи; самостоятельно искать необходимую информацию для решения задачи из различных источников; доопределять условие задачи данными, которые имеются в задаче «между строк»; организовывать найденные данные (составлять модель задачи, используя необходимые и достаточные данные); выявлять противоречие, ориентироваться в избыточном количестве информации. Работа с некорректными задачами ориентирована на развитие выделенных действий.
Результаты опытно-экспериментальной проверки представленного содержания и видов работ доказали их эффективность.
Библиографическая ссылка
Шестакова Л.Г., Безусова Т.А. ФОРМИРОВАНИЕ УМЕНИЯ РАБОТАТЬ С НЕКОРРЕКТНЫМИ ЗАДАЧАМИ (НА МАТЕРИАЛЕ ГЕОМЕТРИИ 10 КЛАССА) // Современные проблемы науки и образования. – 2018. – № 4. ;URL: https://science-education.ru/ru/article/view?id=27800 (дата обращения: 18.04.2024).




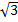 см, а диагональ равна 4 см. Определите его вид»
см, а диагональ равна 4 см. Определите его вид»