Любая человеческая деятельность, наряду с целеполаганием, планированием, организацией и выполнением, предполагает, конечно же, контроль результатов. В равной степени это относится и к обучению, где необходимо измерение уровня учебных достижений обучающегося. Методы для проведения педагогических измерений разрабатываются в рамках современной теории тестирования IRT (Item Response Theory). Есть ведущая идея, в которой является представление о латентных характеристиках: испытуемого – подготовленность, и задания – трудность. Эти две величины измеряются при проведении процедуры тестирования. Наиболее простой моделью измерения в IRT является однопараметрическая модель Г. Раша (Rash Measurement).
По объективным историческим причинам контроль результатов обучения основывается на модели «черный ящик» (ЧЯ) [1]. По определению черный ящик – это объект, внутреннее устройство которого либо неизвестно, либо слишком сложно для того, чтобы можно было по свойствам его составных частей и структуре связей между ними делать выводы о поведении объекта [2, т. 29, с. 107]. Ученик, прошедший обучение, как раз является таким объектом: во-первых, не известно, насколько прочно им были усвоены знания, умения и навыки; во-вторых, он обладает очень сложным «устройством» – нейронной структурой головного мозга, к тому же не поддающейся наблюдению. Таким образом, при контроле ученик считается черным ящиком, и необходимо определить, как он себя ведет в различных проблемных ситуациях. Задача исследователя (экзаменатора) - путем оказания воздействий (предъявление заданий) на ЧЯ (обучающегося) сделать суждение о его свойствах (достигнутом уровне образовательных результатов). Обычно процесс исследования ЧЯ – это последовательность экспериментов. Их результаты заносятся в таблицу – протокол исследования (рис. 1).

Рис. 1. Протокол исследования ЧЯ
После проведения большого количества экспериментов исследователь приступает к поиску закономерностей в поведении ЧЯ. Когда модель ЧЯ применяется к обучающемуся при контроле знаний (например, в тестировании), протоколом исследования является таблица тестовых результатов.
Такой подход приводит к ряду проблем [3]. Во-первых, для исследования ЧЯ экспериментальным путем с ведением протокола исследования необходимо большое количество испытаний. Контроль становится длительным, а количество заданий, необходимых для получения оценки, возрастает. Во-вторых, отсутствует предварительная оценка уровня подготовленности обучающегося. В процессе обучения обычно накапливается некоторая информация об успешности учеников. Однако в протоколе исследования ЧЯ этой информации места нет. В-третьих, контроль отделяется от обучения, становясь отдельным процессом. Из-за этого невозможно получение представления об уровне подготовки обучающегося без проведения обособленной процедуры (тестирования, опроса, контрольной работы и т.п.), с последующим анализом протокола.
Выходом из сложившейся ситуации может оказаться переход от контроля, построенного на анализе протокола исследования ЧЯ, к методам, базирующимся на моделях когнитивных свойств обучающегося. Такую модель в кибернетике обычно называют «белый ящик». Белый ящик (БЯ) – это объект, обладающий известной структурой. БЯ, при достаточно сложном устройстве, может быть настроен так, чтобы преобразовывать входной сигнал, так же как и ЧЯ. Таким образом, выделяются два способа исследования ЧЯ: ведение протокола с последующим его анализом и создание модели, обладающей аналогичными свойствами. В образовательном процессе второй способ является более предпочтительным, потому что использование БЯ позволяет нивелировать трудности, возникающие при протоколировании экспериментов с ЧЯ.
Для того чтобы модель обучающегося правильно отражала его когнитивные свойства, необходима ее настройка под ученика. Это может быть осуществлено в процессе обучения, что выгодно отличает этот подход от противоположного. Информация об успешности ученика в процессе обучения естественным образом будет отражена и накоплена в его модели. Это полностью снимает парадоксальность первого подхода к исследованию ЧЯ. Под словом «модель» здесь, в первую очередь, подразумевается компьютерная модель, реализуемая средствами ЭВМ. Поэтому контроль по модели обучающегося, представленной в виде компьютерной программы, может происходить практически мгновенно и без непосредственного присутствия обучающегося.
Когда речь идет об обучении, нет необходимости получать полный операционный эквивалент ученика (создание интеллектуальных агентов - это задача искусственного интеллекта). В этом случае под БЯ следует понимать модель ученика, отражающую его знания, умения и навыки. Ее назначение заключается в предоставлении информации об уровне достигнутых образовательных результатов. При таком подходе контроль превращается в процесс анализа модели обучающегося, протекающий в недрах ЭВМ, параллельно с обучением. Это возможно тогда, когда параметры модели непрерывно корректируются, чтобы наилучшим образом соответствовать обучающемуся.
Цель исследования
Перспективной для создания простого БЯ представляется однопараметрическая модель педагогических измерений Г. Раша (Rash Measurement) ввиду того, что в ней фигурирует параметр подготовленности. Именно он является простейшей моделью ученика. Однако традиционное применение модели Г. Раша является исследованием ЧЯ с помощью ведения протокола. Это так, потому что подготовленность обучающегося вычисляется по таблице тестовых результатов – протоколу исследования ЧЯ. Чтобы использовать Rash Measurement для создания БЯ, необходим способ определения подготовленности обучающегося в любой момент времени. Целью работы является разработка способа динамического определения латентных характеристик, фигурирующих в Rash Measurement, в процессе обучения, без применения процедуры тестирования.
Материалы и методы исследования. Для достижения поставленной цели рассмотрим модель педагогического измерения Г. Раша. Успех при выполнении задания в большей степени определяется разностью подготовленности обучающегося и трудности задания. Функция, определяющая вероятность правильного выполнения задания, была предложена Г. Рашем в 1960 г.:
|
|
(1) |
где:
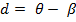 ,
,
θ – параметр подготовленности испытуемого;
β – параметр трудности задания.
Коэффициент 1,7 в показателе экспоненты введен для наилучшего совпадения функции (1) с интегральной функцией нормального распределения [4, с. 471].
График функции (1) – характеристическая кривая – представлен на рис. 2.
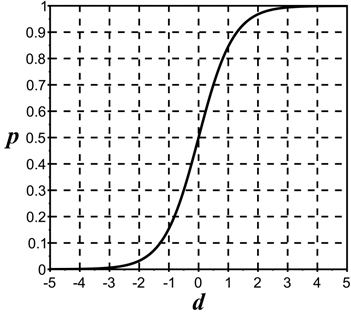
Рис. 2. Характеристическая кривая Г. Раша
Величины θ и β измеряются по единой шкале логитов и вычисляются по таблице тестовых результатов (матрице ответов). Определяющая θ формула такова:
|
|
(2) |
где:
pi – доля верных ответов i-го испытуемого на все задания теста;
qi – доля ошибочных ответов i-го испытуемого на все задания теста.
Трудность j-го задания βj вычисляется аналогично:
|
|
(3) |
где:
qj – частота ошибочных ответов испытуемых на j-е задание;
pj – частота верных ответов испытуемых на j-е задание.
Для иллюстрации можно привести подробный пример вычислений θ и β, представленный в работе [5]. Теоретически значения θ и β лежат в интервале (–∞; +∞). Однако их реальные значения, определенные в логитах, могут находиться в диапазоне от -5 до 5. Очевидно, что если обучающийся с заявленным уровнем подготовленности θ выполняет предложенное задание, соответствующее его уровню подготовленности, то этот факт дает основание сделать заключение о том, что его истинная подготовленность превосходит θ. В противоположном случае можно сделать заключение о том, что истинная подготовленность ниже заявленной θ. Аналогичные рассуждения можно провести для параметра трудности задания. Эти умозаключения позволяют проводить корректировку параметров подготовленности обучающегося и трудности задания путем придания приращений?корректировок.
Результаты исследования. Для динамической параметризации, т.е. непрерывного вычисления параметров θ и β, примем следующие правила. Формула для корректировки параметра θ имеет следующий вид:
|
|
(4) |
где
|
|
(5) |
здесь θnew и θold – новое и старое значения этого параметра соответственно;
kθ – максимально возможное приращение величины θ;
p – вероятность успешного выполнения задания, вычисленная по формуле (1);
δ – результат выполнения задания испытуемым;
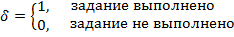 .
.
Корректировка трудности задания в таком случае проводится по формуле:
|
|
(6) |
где
|
|
(7) |
величины βnew и βold – новое и старое значения β соответственно;
kβ – максимально возможное приращение β.
Графики приращений Δθ и Δβ представлены на рис. 3.
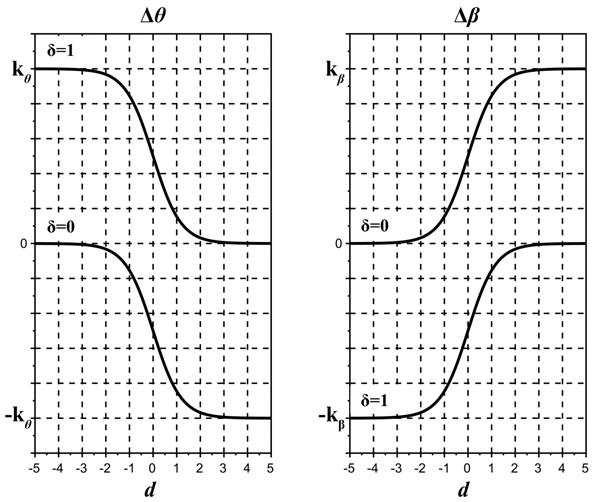
Рис. 3. Графики приращений параметров θ и β для различных исходов решения задачи (значений δ)
Обсуждение результатов. Если d > 5, т.е. уровень подготовленности обучающегося существенно больше параметра трудности задания, то при правильном выполнении задания θ изменится незначительно. Та же ситуация будет наблюдаться, когда d < –5, т.е. трудность задания значительно превосходит уровень подготовленности обучающегося, и при этом оно не будет выполнено. Эти пограничные ситуации являются самоочевидными, и корректировка параметров в них, вероятно, вообще не требуется. В этих случаях приращения могут обратиться в нуль при пропорциональном переходе от шкалы логитов к какой-либо более удобной, целочисленной шкале. Максимальные приращения получают параметры, если d > 5, т.е. когда уровень подготовленности испытуемого существенно больше трудности задания, но при этом оно не будет выполнено. Так же, если d < –5, т.е. трудность задания много больше подготовленности обучающегося, однако при этом оно выполнено верно. Все промежуточные ситуации также логичны. Выполняя трудное задание, ученик получает большее приращение параметра подготовленности, чем при легком задании. То же относится и к заданиям.
Несмотря на то что величины θ и β измеряются в одинаковых единицах, между ними есть принципиальное отличие. Если задание не изменяется, то, очевидно, его истинная трудность имеет постоянное значение. Поэтому в процессе многочисленных корректировок по предложенной схеме значение β должно сходиться к некоторому значению – истинному значению трудности данного задания. Обучающийся, если рассматривать его на протяжении всего процесса обучения, имеет переменное значение подготовленности θ. Поэтому мониторинг этого параметра должен быть непрерывным. Непрерывность в данном случае означает не проведение частых проверок, но интеграцию контроля с процессом обучения. При этом выполняемые учебные действия учитываются для корректировки модели обучающегося.
Предложенный способ коррекции параметра подготовленности обучающегося пригоден для геймификации процесса обучения [6]. Под которой обычно понимают применение подходов, характерных для компьютерных игр, для неигровых процессов с целью привлечения пользователей и потребителей, повышения их вовлеченности в решение прикладных задач [7]. В этом плане непрерывное вычисление параметра подготовленности может рассматриваться как игровая механика (рейтинг, очки, баллы и т.п.). Таким образом, это позволяет ставить игровые цели (например, достижения определенного значения параметра θ). Игровые цели будут явно коррелировать с образовательными, потому что повышение значения параметра подготовленности происходит при выполнении реальных упражнений (способствующих достижению целей обучения). Кроме этого, непрерывный мониторинг числовой оценки каждого обучающегося и публичный доступ к его значениям всех обучающихся может привести к возникновению эффекта соревновательности между обучающимися.
Выводы. Несмотря на то что существуют более точные модели педагогических измерений, для многих ситуаций однопараметрическая модель Г. Раша является вполне достаточной. При этом более развитые модели оказываются избыточными и неоправданно сложными. Так, в двухпараметрической модели А. Бирнбаума в показателе экспоненты (1), помимо разности (θ – β), содержится дополнительный множитель – дифференцирующая способность задания. В случае когда изучение каждого задания нерационально, допустимо считать, что все они имеют одинаковую дифференцирующую способность. Трехпараметрическая модель А. Бирнбаума, также учитывает вероятность угадывания ответа. Если же использовать задания открытого типа, вероятность угадать правильный ответ пренебрежимо мала, и ее можно вовсе не учитывать.
Заключение. Таким образом, в работе предложен путь решения проблем, возникающих при исследовании модели ЧЯ, применяемой в контроле образовательных результатов, с помощью ведения и анализа протокола. Решение заключается в переходе от протоколирования экспериментов с ЧЯ к построению «белого ящика» – модели обучающегося. В качестве такой простейшей модели указан параметр подготовленности обучающегося, входящий в модель Г. Раша. Разработан способ динамического определения как этого параметра, так и трудности учебного задания. Суть метода заключается в динамической корректировке рассмотренных параметров, посредством придания приращений-корректировок, после каждого учебного действия. Представлены графики введенных корректировок при различном соотношении исходных значений параметров.
Библиографическая ссылка
Асауленко Е.В. ДИНАМИЧЕСКАЯ ПАРАМЕТРИЗАЦИЯ В RASH MEASUREMENT // Современные проблемы науки и образования. – 2018. – № 3. ;URL: https://science-education.ru/ru/article/view?id=27707 (дата обращения: 25.04.2024).




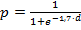 ,
,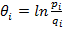 ,
,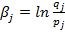 ,
, ,
,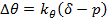 ,
,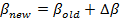 ,
,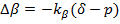 ,
,