При рассмотрении задачи поиска в больших системах как правило рассматривается модель метрического пространства, элементами которого представлены все допустимые результаты поиска и все корректные запросы. При этом оказывается возможным построение нечетких алгоритмов поиска ближайших соседей и тем самым решение задач кластеризации для самообучения системы [1].
Однако нередко постановка задачи не допускает корректного введения метрического пространства, являющегося объединением множеств как ответов, так и запросов в системе. В этом случае, как правило, эти множества рассматриваются сепаративно и система описывается множеством пар типа (вопрос, ответ). При этом задается отношение на множестве таких пар с помощью некоторой скалярной неотрицательной функции, называемой обычно функцией релевантности [2]. Значение этой функции определяют насколько второй элемент пары (данный ответ) соответствует первому элементу пары (запросу). В настоящей работе предлагается алгоритм поиска ответов с максимальной релевантностью для любого допустимого запроса.
Пусть задано два конечных множества
![]() , имеющее семантический смысл запросов некоторой предметной области, и
, имеющее семантический смысл запросов некоторой предметной области, и
![]() , имеющее семантический смысл ответов на запросы в этой же предметной области.
, имеющее семантический смысл ответов на запросы в этой же предметной области.
Определено отношение XÒY называемое отношением релевантности, такое, что каждому элементу из множества запросов соответствует подмножество так называемых релевантных ответов из множества
![]()
В этом случае можно ввести функцию релевантности rel
![]()
Эта функция аналогична используемой обычно функции “похожести” – similarity , используемой в тех случаях, когда запрос и ответ рассматриваются как элементы одного и того же множества. В таких случаях можно считать это множество наделенным структурой метрического пространства или близкого к такому. Для решения задач поиска в метрических пространствах создан целый ряд мощных инструментов, основанных на различных математических свойствах таких пространств. Нашей же целью является решение задачи поиска для случая, когда множества запросов и ответов затруднительно представить элементами одного и того же метрического пространства.
Сведем задачу максимизации релевантности к задаче дискретного программирования. Иногда вместо задачи на максимум выгоднее рассматривать задачу минимизации. С этой целью будем рассматривать вместо функции релевантности связанную с ней функцию расстояния релевантности
![]()
![]()
Задача: найти алгоритм отыскания максимально релевантной точки
![]()
В изложенной постановке задача относится к классу трудноразрешимых задач дискретной оптимизации [3].
Основной идеей этого раздела является попытка свести задачу на поиск релевантного ответа из Y на запрос из X при известной функции релевантности rel ( . , . ) к нескольким задачам локального поиска на множестве Y. В основу метода мы положим оснащение этого множества графом со специальными свойствами, известными как MSW (MetrizedSmallWorld) для поиска локального минимума [4].
Классический подход применения метода локальной оптимизации сводится к наделению множества Y любой произвольной метрикой, назначением начальной точки и радиуса окрестности локального поиска. Алгоритм поиска минимума в этом случае сводится к поиску локального минимума в выбранной окрестности и перехода к новой начальной точке, в качестве которой назначается найденная на предыдущем локальном шаге точка минимума.
Как показано в [5], если на дискретном множестве существует функция расстояния, то на нем может быть построен граф, обладающий свойствами тесного мира (MSW граф). То есть расстояние между любыми вершинами такого графа в среднем оценивается логарифмической величиной от размера графа, числа его вершин. При этом существует простой алгоритм жадного поиска, приводящий в среднем за логарифмическое число шагов к отысканию ближайших соседей для любого вновь выбранного элемента y0 из множества (поглощающего)![]() .
.
Наделенного той же функцией расстояния. Выбрав произвольно начальную точку из Y можно найти в Y ближайших соседей для y0 совершив логарифмически связанное с размером Y число локальных поисков.
Сведем нашу задачу поиска элемента из множества ответов Y релевантного заданному запросу из X к задаче поиска на MSW графе.
Пусть задан элемент ![]() и MSW граф на Y. Задана также вычислимая функция расстояния релевантности между X и Y
и MSW граф на Y. Задана также вычислимая функция расстояния релевантности между X и Y
![]()
Задача: найти алгоритм отыскания максимально релевантной точки
![]()
Основная идея алгоритма может быть представлена следующим образом:
Сначала назначим случайным образом точку y0 в Y – одну из вершин графа MSW, построенного на Y.
Найдем расстояние релевантности между этой точкой и x*.
![]()
Рассмотрим все вершины графа, являющиеся соседями y0 , и найдем расстояния релевантности до них. Выберем ту вершину, расстояние релевантности до которой от x* минимально. Сравним это расстояние с значением d0: если найденное расстояние меньше, то выбираем новую соответствующую ему вершину за новую начальную точку поиска и повторяем поиск максимально релевантной точки среди ее соседей, если нет, то выбираем точку y0 в качестве решения задачи – возвращаем как максимально релевантную запросу x* в данном цикле поиска. После этого выбирается другая случайная точка y0 в Y и процесс поиска повторяется. Число случайных поисков может быть выбрано заранее или определяться адаптивно в зависимости от разброса найденных Среди всех найденных точек локального минимума выбираются те, которые имели минимальное расстояние релевантности и это подмножество объявляется решением. В большинстве случаев такое подмножество состоит из единственного элемента и в этом случае найденное решение строго соответствует поставленной задаче.
В приведенном выше подходе остается неизвестным и принципиально важным вопрос о построении MSW графа на множестве Y. Очевидно, что поскольку на этом множестве не задана функция метрики, то мы можем назначить ее произвольно. Но также очевидно, что от ее выбора будет сильно зависеть эффективность работы алгоритма. Мы предлагаем здесь выбрать в качестве функции метрики некоторую функцию внутреннего расстояния на Y, индуцированного расстоянием релевантности. Основная идея подхода состоит в том, что в множестве X некоторым образом выбирается подмножество из M “представительных” элементов, далее называемый базисом в X. Обозначим это подмножество.
Определим для каждой точки из Y расстояния релевантности
![]()
Назовем полученный для каждого k набор чисел координатами элемента yi в системе координат XB. Таким образом на множестве Y индуцируется координатная сетка размерности M. Теперь определим функцию внутреннего расстояния на Y с помощью этой координатной системы, задавая ее значения как:
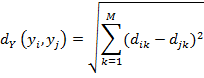
Можно видеть, что такая функция удовлетворяет всем основным аксионам расстояния, поскольку дает нулевое значение для совпадающих точек в Y и положительна для несовпадающих. Мы не будем давать здесь анализ выполнения неравенства треугольника для индуцированной функции расстояния, поскольку это не является существенным для дальнейшего, однако заметим, что при правильном выборе множества XB введенная функция расстояния удовлетворит всем аксиомам метрики.
Рецензенты:
Соколова Э.С., д.т.н, зав. кафедрой «Информатики и систем управления» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород;
Хранилов В.П., д.т.н., профессор, заместитель директора ИРИТ по научной работе НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Библиографическая ссылка
Бритвина Е.В. АЛГОРИТМ САМООРГАНИЗАЦИИ ПРОСТРАНСТВА ПОИСКА В БОЛЬШИХ СИСТЕМАХ С НЕЧЕТКИМ ВЫБОРОМ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=17176 (дата обращения: 16.04.2024).



