Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

   Одним из значимых приложений методов цифровой фильтрации является решение задач выделения особенностей, расчета характеристик и определения параметров изображений. Часто на основе признаков и атрибутов изображений решаются задачи более высокого уровня, например, задачи распознавания [9, 10]. При этом требуется высокая точность выделения объектов интереса  на изображении для точного определения их характеристик и формирования векторов признаков , часто являющиеся исходными данными в процедурах идентификации и классификации [5, 7, 8]. В этой связи актуальными остаются задачи разработки алгоритмов фильтрации объектов изображений [2–4].

   При выделении объектов  изображений эффективными являются методы многомасштабной обработки, позволяющие анализировать характеристики  этих объектов на множестве уровней разложения , при смене которых свойства разных объектов могут проявляться более отчетливо [3].

   Объекты изображений с точки зрения распределения функции яркости можно трактовать как локальные неоднородности (особенности) двумерных сигналов. Удобным математическим инструментом выделения локальных особенностей сигналов и их анализа является непрерывное вейвлет-преобразование, обладающее также всеми преимуществами многомасштабной обработки.

   Возможность использования непрерывного вейвлет-преобразования для выделения объектов обусловлена тем свойством, что при сопоставимых размерах особенности и фильтра амплитуда вейвлета, соответствующего области особенности, будет стремиться к максимуму. Это свойство действительно как для одномерных, так и для двумерных вейвлетов.

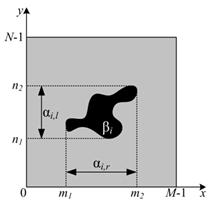
Рис. 1.  Пример особенности изображения, обладающей анизотропными характеристиками

 

  Поскольку локальные особенности  изображений являются двумерными, то очевидно, что они могут обладать анизотропными характеристиками , например, размеры неоднородности по каждому из направлений просмотра изображения могут существенно различаться (рис. 1).

В этом случае для фильтрации особенностей целесообразно использовать сепарабельное вейвлет-преобразование, реализуемое на основе:

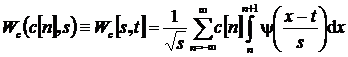
отдельно по строкам  и столбцам  изображения . При этом, фильтрация каждой особенности будет заключаться в фильтрации особенностей одномерных сигналов, соответствующих строкам или столбцам изображения, на которых эти особенности проявляются.

   Такая постановка задачи, очевидно, позволяет разрабатывать алгоритмы фильтрации с выбором масштабирующего коэффициента  адаптивно к размеру поперечного сечения особенности  в заданной точке и направлении.

Другим возможным подходом к фильтрации подобных особенностей является использование двумерного непрерывного вейвлет-преобразования вида:

, .

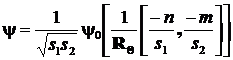   Одним из возможных вариантов используемого при этом вейвлета  может служить вторая производная функции Гаусса (так называемый вейвлет «мексиканская шляпа»), обобщенная на двумерный случай 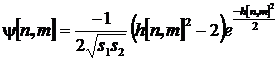[1]:

,                                                                                    (1)

где 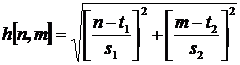, с возможностью поворота вейвлета на угол , т.е. .

Из (1) следует, что возможно задание двух различных масштабирующих коэффициентов , , что приводит к различной степени сжатия вейвлета  по двум осям (рис. 2).

  

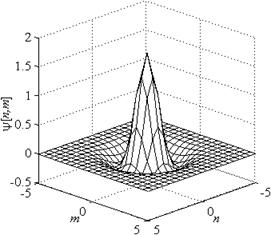
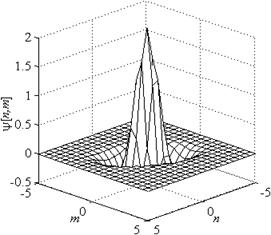
а)                                                                    б)

Рис. 2. Аналоги вейвлета «мексиканская шляпа» для двумерного случая

при: а – , , ; б – , ,

 

Тогда, очевидно, что, используя вейвлет вида (1), возможна фильтрация особенностей с различными размерами по двум направлениям, которые могут быть заданы углом поворота вейвлета.

Фильтрация особенностей изображений – задача важная, возникающая во многих приложениях цифровой обработки. Наряду с задачами определения характеристик  выделяемых объектов , например, в задачах распознавания, интерес представляет задача определения некоторых связей (топологических, пространственных и др.) между объектами изображения и их отнесения к некоторой группе объектов , на основе анализа полученных зависимостей.

Определение 1. Группой объектов  или групповым объектом назовем множество объектов  изображения, обладающих схожими характеристиками  или расположенных на незначительном удалении друг от друга.

Определение 2. Одиночный объект , входящий в некоторую группу объектов , назовем элементарным объектом или символом.

Таким образом, возникает задача фильтрации групповых объектов изображений, состоящих их множества элементарных объектов или символов  [4, 6], т.е. , .

   При обработке изображений групповых объектов часто необходимо получать и анализировать характеристики группы образов в целом, а не отдельных элементарных объектов. При этом необходимо определить, какие элементарные объекты   принадлежат той или иной группе . Единого критерия отнесения элементарного объекта изображения к групповому не существует. Для каждой задачи формируется свой параметр. Принадлежность элементарного объекта групповому может быть определена на основе вычисления некоторого набора характеристик элементарных символов. При этом возможны два варианта решения задачи: определение характеристик элементарных объектов и сравнение их с некоторыми пороговыми значениями или же использование некоторого оператора классификации , не учитывающего характеристики отдельных элементарных символов , но относящего их к какой-либо группе объектов , т.е. , , .

Определение 3. Под фильтрацией групповых объектов, в данном случае, будем понимать реализацию некоторого оператора , относящего каждый элементарный объект  некоторого множества  к определенной группе объектов  и формирующего соответствующее представление каждой группы для последующего анализа и решения задач обработки изображений.

    Использование операторов, не учитывающих характеристики элементарных символов, при анализе изображений естественных объектов более предпочтительно. Это обусловлено следующей причиной. Естественные образы чаще всего обладают уникальными характеристиками, поэтому задача отнесения элементарного объекта  к некоторой группе  затрудняется необходимостью анализа множества признаков  каждого такого объекта. Другими словами эта задача сводится к задаче классификации элементарных символов. Использование оператора классификации  позволяет рассматривать характеристики всего изображения  и на основе их анализа относить каждый элементарный объект к определенному групповому, т.е. . При этом отпадает необходимость в анализе уникальных признаков элементарных символов и выполнении сложных операций их классификации.

   Возможным критерием отнесения элементарных символов  к групповому объекту  является их пространственное расположение и максимальное расстояние между каждой парой соседних элементарных объектов.

   Очевидным решением этой задачи является определение расстояний между парами соседних объектов и сравнение полученных расстояний с пороговым значением. Недостатком данного подхода является необходимость расчета характеристик  каждого объекта  изображения (например, центра тяжести и расстояния между центрами тяжести пар объектов), кроме того, необходимо определить какие объекты изображения являются соседними. При достаточно большом количестве объектов  на изображении эта задача является весьма трудоемкой. Поэтому более предпочтительным является использование подхода, не использующего для классификации характеристики элементарных объектов.

Возможным путем решения этой задачи также может служить использование вейвлет-преобразований. Поскольку анализ амплитуд вейвлетов  позволяет обнаруживать одиночные локальные неоднородности  изображений, то вероятно, что при увеличении масштабирующего коэффициента  вейвлет-преобразования на некоторую величину, максимумы амплитуд вейвлетов будут соответствовать областям изображения, содержащим группы  элементарных объектов . Тогда для успешного решения задачи фильтрации групповых объектов, необходимо проведение анализа вейвлет-образов , соответствующих некоторому множеству масштабов , с установлением связей между максимумами амплитуд на соседних уровнях разложения  и .

Рецензенты:

 

Андрианов Д.Е., д.т.н., доцент, заместитель директора по учебной работе, заведующий кафедрой «Информационные системы», Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Муром;

Орлов А.А., д.т.н., доцент, заместитель директора по развитию электронного обучения и дистанционных образовательных технологий, заведующий кафедрой «Физика и прикладная математика», Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Муром.