Применение квантовой статистики для электронов проводимости в металле позволяет развивать количественную теорию удельного электросопротивления (УЭС) металлов. Прогресс в развитии теории свойств отдельных металлов связан с развитием псевдопотенциальной теории. Существенно, что при исследовании электросопротивления не нужно знать закон дисперсии 
во всей зоне Бриллюэна, поскольку важны лишь электроны возбуждаемые термически. К ним относятся электроны с энергией порядка 
вблизи уровня Ферми. Остальные электроны системы вследствие принципа Паули не участвуют в рассеянии. Использование псевдопотенциальной теории позволяет проводить расчеты электросопротивления и сплавов с учетом как стационарных, так и нестационарных искажений решетки. В работе исследуется возможность использования теории псевдопотенциалов, одноэлектронного приближения, сферической поверхности Ферми, линейной теории экранирования для моделирования температурной зависимости УЭС многоэлектронного металла на примере алюминия.
Температурная часть удельного электросопротивления (УЭС) в рамках теории псевдопотенциалов
Удельное электросопротивление монокристаллического металла в зависимости от температуры в модели псевдопотенциалов с использованием второго порядка теории возмущения и линейной теории экранировании при идеальной кристаллической структуре металла имеет вид
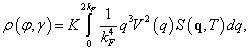(1)
где
углы в полярной системе координат вектора рассеяния электрона 
, 
- температурный структурный фактор,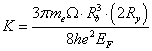 
- коэффициент, зависящий от мировых констант и характеристик металла при заданном объеме, 
- объем, приходящийся на атом в атомных единицах, 
- энергия Ферми металла в атомных единицах, 
- масса электрона в системе СИ, 
- радиус Бора в системе СИ, 
- энергия Ридберга в системе СИ, 
- квадрат экранированного псевдопотенциала металла в атомных единицах, характеризующего вероятность перехода квазиэлектрона из состояния с вектором 
, в состояние 
на поверхности Ферми, 
- удельное электросопротивление монокристаллического металла в системе СИ [5].
Температурную часть УЭС поликристалла можно вычислить, усредняя температурный структурный фактор по всем направлениям вектора рассеяния q. УЭС поликристалла, после усреднения по всем углам вектора q, имеет вид:
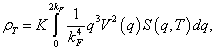(2)
- УЭС поликристаллического металла в системе СИ в зависимости от температуры.
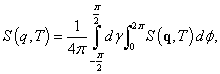(3)
где 
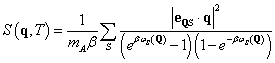, (4)
- усредненный по направлениям вектора рассеяния температурный структурный фактор поликристаллического металла, 
- вектор фонона, ZB – зона Бриллюэна, 
, 
- постоянная Больцмана, Т – температура Кельвина, 
- нормальные частоты колебаний атомов металла соответствующие вектору фонона 
, S – индекс поляризации частоты, 
- собственный вектор соответствующий собственной частоте колебаний атомов металла.
Знаменатель в выражении для структурного фактора 
обладает трансляционной симметрией. Трансляционная симметрия знаменателя структурного фактора связана с трансляционной симметрией частот колебаний атомов - 
. При численных расчетах нормальных частот колебаний атомов через динамическую матрицу в идеальном металле трансляционная симметрия учитывается автоматически. В результате выражение (2) можно привести к интегралу по безразмерной переменной 
для расчета УЭС поликристалла
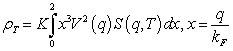, (5)
здесь 
- безразмерный структурный фактор, усредненный по всем ориентациям волнового вектора рассеяния q (3). В нашем случае мы рассматриваем ГЦК структуру алюминия. Формула (5) справедлива в рамках принятых приближений для всех температур твердого состояния металла, при фиксированной структуре.
Нормальные процессы и процессы "переноса"
При аналитических оценках УЭС с использованием моделей колебаний атомов Дебая или Эйнштейна (в которых не учитывается трансляционная симметрия частот колебаний атомов кристаллической решетки) необходимо различать два процесса взаимодействия квазиэлектрона с фононами: нормальный процесс рассеяния и процесс "переброса". Квантово-механические процессы рассеяния электронов на эффективных потенциалах атомов обсуждались в работе [1]. Рассматривались нормальные процессы, при которых 
, и процессы "переброса", при которых 
.
На Рис.1 приведена графическая иллюстрация этих процессов. Переходы квазиэлектрона из одного состояния в другое в соответствии с принципом Паули осуществляются только электронами, находящимися почти на поверхности Ферми, то есть при 
и 
. Эффективный потенциал, характеризующий вероятность перехода квазиэлектрона из состояния с вектором в состояние с вектором , зависит только от угла θ между векторами и или от модуля вектора рассеяния , так как существует связь между θ – углом рассеяния квазиэлектрона и q - модулем вектора рассеяния 
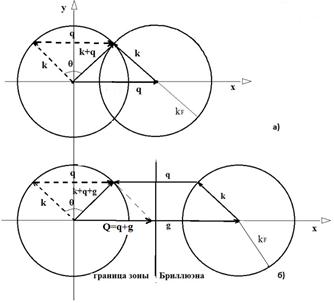
На Рис.1а приведена графическая иллюстрация нормального процесса рассеяния, при котором вектор рассеяния равен волновому вектору фонона. На Рис.1б приведена графическая иллюстрация процесса "переброса", при которых волновой вектор фонона 
. Не зависимо от того, где находится вектор фонона в зоне Бриллюэна или нет, аргумент формфактора псевдопотенциала равен модулю разности фермиевских векторов рассеяния электрона 
.
В данной работе нормальные частоты 
и собственные вектора 
вычислялись с помощью численной диагонализации динамической матрицы, полученной в приближении Борна-Бегби с использованием экспериментальных значений упругих постоянных 
ГЦК кубического кристалла ГЦК алюминия [2]. Это позволяет автоматически учитывать процессы "переброса" при расчете УЭС. 
- динамическую матрицу ГЦК-металла получали по формулам из [2]
, 
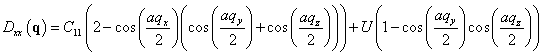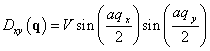, (6)
, 
,
- постоянная кубической решетки, 
проекции вектора на оси координат.
Остальные значения динамической матрицы получаются с помощью циклической перестановки индексов. Расчет УЭС от температуры проводился в двух моделях эффективного рассеивающего потенциала: модели гладкого нелокального модельного псевдопотенциала (ГНМП) [3,4] и модели квазилокального псевдопотенциала Хейне-Абаренкова-Анималу (ХАА) [7,8,10].
Анализ различия теоретических и экспериментальных данных
Теоретические значения температурной части УЭС в широком диапазоне температур в двух моделях и экспериментальные значения [9] показаны на Рис.2. Параметры ГНМП, использованные для расчета УЭС, приведены в Таблице.
Параметры ГНМП алюминия
|
OM |
RM |
EF |
EC |
A0 |
A1 |
A2 |
D0 |
D1 |
D2 |
ZDP |
|
|
Al |
111.4 |
3.0 |
0.4299 |
0.0925 |
-2.307 |
-1.126 |
3.272 |
-1.227 |
-0.614 |
0.751 |
-0.124 |
Результаты расчета, полученные в модели ГНМП, сравнивались с расчетами в модели ХАА. Модель ГНМП дает более близкие к экспериментальным данным значения УЭС по сравнению с моделью ХАА (Рис.2).
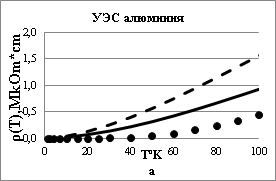
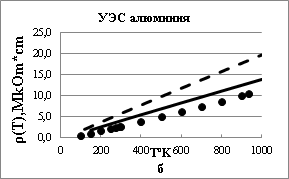
Отличие экспериментальных данных от теоретических в модели ГНМП можно объяснить применением приближения сферической формы поверхности Ферми. В многоэлектронном алюминии поверхность Ферми значительно отличается от сферы. Учет истинной поверхности Ферми при расчете УЭС алюминия требует кропотливых численных расчетов.
Ошибки в расчеты УЭС могут вносить так же и, полученные теоретически, фононные спектры металла. В настоящей работе применялась модель Борна-Бегби, то есть модель нецентральных сил с учетом взаимодействия на первой координационной сфере [2], при этом использовались экспериментальные значения упругих постоянных 
1.068
Н/
0.607Н/
,
0.282Н/, полученные экспериментально при 300ºК [6].
Для анализа причин различия теоретических значениях УЭС алюминия в двух моделях следует рассмотреть зависимость от 
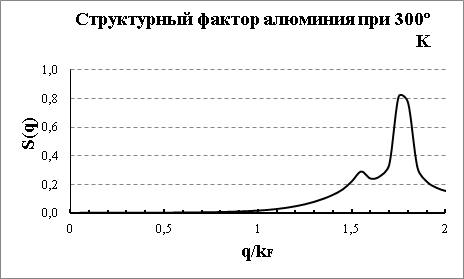
формфакторов псевдопотенциалов и подинтегральных выражений в двух моделях при расчете УЭС (6) от . На Рис.3 приведена зависимость структурного фактора алюминия при температуре 300ºК, полученная в приближение нецентральных сил с учетом ближайших соседей для кубической ГЦК решетки алюминия. Из Рис.3 видно, что наибольшие значения 
имеет при 
. Такое поведение структурного фактора объясняется процессами "переброса", которые существенны при 
. В этом случае знаменатель структурного фактора (3) стремится к нулю при 
в случае процесса "переброса", то есть вектор фонона находится в районе вектора обратной решетки. Как результат структурный фактор имеет максимумы в области, где 
. При усреднении по углу (3) эта область размывается. Первый максимум структурного фактора обусловлен вектором обратной решетки 
, 
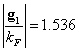, а второй – вектором 
, 
,
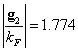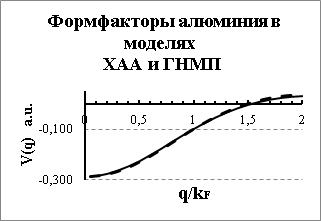
На Рис.4 показана зависимость формфактора алюминия от в области 
. При 
значения квадрата формфактора в модели ХАА несколько выше формфактора ГНМП. Это приводит к тому, что подинтегральные функции УЭС алюминия в двух моделях значительно отличаются в этой области из-за наличия весового множителя пропорционального
. Различие значений подинтегральных функций в разных моделях (Рис.5) приводит к значительно разным результатам моделирования УЭС. При значения квадрата формфактора в модели ХАА несколько выше формфактора ГНМП. Это приводит к тому, что подинтегральные функции УЭС алюминия в двух моделях значительно отличаются в этой области из-за наличия весового множителя пропорционального. Различие значений подинтегральных функций в разных моделях (Рис.5) приводит к значительно разным результатам моделирования УЭС.
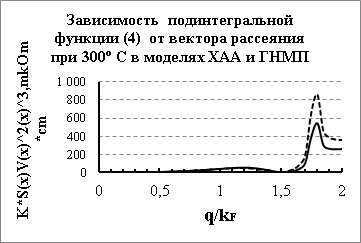
Использование ГНМП значительно приближает теоретические значения УЭС алюминия к экспериментальным данным по сравнению с расчетами в рамках квазилокального потенциала ХАА.
Заключение
В работе выполнен теоретический расчет температурной части УЭС алюминия в двух моделях: в модели квазилокального потенциала ХАА и в модели ГНМП. При моделировании УЭС алюминия использовался метод Борна-Бегби расчета динамической матрицы колебаний атомов металла [2]. Сравнение экспериментальных значений температурной части УЭС алюминия с теоретическими значениями позволяет сделать следующие выводы:
· при моделировании температурной части УЭС можно использовать псевдопотенциалы, приближение второго порядка теории возмущения и линейную теорию экранировании;
· наиболее близкие значения УЭС к эксперименту при теоретическом расчете температурной части УЭС дает использование нелокального потенциала;
· основную роль при расчете УЭС алюминия играют значения псевдопотенциала в области ;
· требуется дополнительный анализ влияния несферичности поверхности Ферми многоэлектронных металлов на моделирование УЭС алюминия.
Рецензенты:
Прокошев В.Г., д.ф.-м.н., профессор, первый проректор, проректор по научной и инновационной работе Владимирского государственного университета, г. Владимир;
Аракелян С.М. д.ф.-м.н., профессор, заведующий кафедрой физики и прикладной математики Владимирского государственного университета, г. Владимир.
Библиографическая ссылка
Крисько О.В., Крисько О.В., Скоробогатова Т.В. РАСЧЕТ ТЕМПЕРАТУРНОЙ ЧАСТИ ЭЛЕКТРОСОПРОТИВЛЕНИЯ АЛЮМИНИЯ С ПОМОЩЬЮ ГЛАДКОГО НЕЛОКАЛЬНОГО МОДЕЛЬНОГО ПОТЕНЦИАЛА (ГНМП) ПРОСТЫХ МЕТАЛЛОВ. // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16773 (дата обращения: 16.04.2024).