Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Распознавание речи с каждым годом находит все большее применение в нашей жизни (цифровая передача и хранение данных, синтез речи, идентификация диктора, устранение дефектов речи, улучшение параметров речевого сигнала), разрабатываются новые алгоритмы. Разработаны модели, описывающие речь ее информационным содержанием, модели, представляющие речь сигналом и т.п. Обработка сигнала представляет собой формирование описания на основе некоторой модели с последующим преобразованием полученного представления. Заключительным шагом является выделение необходимых параметров сигнала, их анализ и работа с ними.

Исторически распространенными классическими методами спектрального оценивания являются периодограммный и коррелограммный методы оценивания спектральной плотности мощности (СПМ) сигнала.

Спектральная плотность мощности (СПМ) стационарного случайного процесса есть дискретно-временное преобразование Фурье (ДВПФ) автокорреляционной последовательности () [2,3].

                                                                                               (1)

Если допустить, что процесс является эргодическим, то:

                                                      (2)

Если определять спектральную плотность мощности исходя из автокорреляционной последовательности, получится коррелограммный метод, поскольку случайный процесс непосредственно не используется для оценки СПМ. В том случае, если использовать саму числовую последовательность для оценки СПМ, получится периодограммный метод.

Оценка СПМ, получаемая на основе коррелограммного метода, принимает форму:

                                                                                   (3)

Среднее значение этой оценки будет сверткой истинного спектра и спектра окна W(f) :

                                              (4)

Правильный выбор окна позволит уменьшить растекание спектра и его смещение.

При наличии конечного множества данных x(n),  и единственной реализации, это соотношение преобразуется в СПМ выборки или периодограмму [2,3]:

 =  =       .                     (5)

На рисунке (1) представлены оценки СПМ периодограммным методом Уэлча без усреднения и с усреднением по 18  сегментам соответственно. Усредненная оценка имеет гораздо меньшую дисперсию, однако пришлось пожертвовать разрешением спектральных компонент. На графике  слева изображена оценка СПМ суммы двух комплексных экспонент с относительными частотами 0.35 и 0.36 периодограммой Уэлча, 1 сегмент – длина окна 1000 отсчетов, SNR=6. Справа – периодограмма Уэлча, 18 сегментов – длина окна 100 отсчетов, сдвиг сегмента 50 отсчетов, SNR=6.

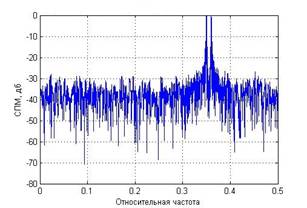
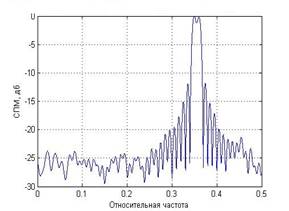
Рис.1. Влияние усреднения на качество периодограммного метода оценивания СПМ

В данном примере использовалось прямоугольное окно. Ширина его главного лепестка уже, чем, например, у окна Хэмминга, поэтому и разрешение спектральных компонент эффективнее. Применение окна уменьшает эффекты просачивания и маскировки вследствие того, что уширение главного лепестка спектра окна происходит за счет уменьшения уровней боковых лепестков. Качество разрешения зависит от количества взятых отсчетов. Аналогичная ситуация и в коррелограммных оценках СПМ близких гармоник. Но имеются некоторые особенности.

Многие случайные процессы дискретного времени описываются следующей моделью [4]:

x[n]= + =                                (6)

Это можно представить в виде выхода фильтра, где x[n] – входная последовательность каузального фильтра, u[n] – входная возбуждающая последовательность (белый шум с нулевым средним и дисперсией ), h[n] – импульсная характеристика фильтра,  a[k] – коэффициент авторегрессии, b[k] – коэффициент скользящего среднего.

Процесс на выходе фильтра (8) соответствует модели авторегрессии – скользящего среднего (АРСС), где параметры a[k] характеризуют авторегрессионную часть этой модели порядка р, а параметры b[k] – ее часть, соответствующую скользящему среднему порядка q[4].

Спектральная плотность мощности для АРСС процесса имеет вид

                                                                                                      (7)

                                                       A(f)=1+ ,                                    (8)

                                                      B(f)=1+ ,                                      (9)

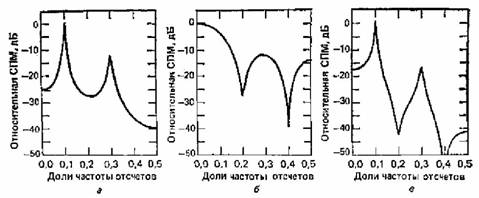
Рис. 2. Примеры оценивания СПМ сигнала с использованием параметрических методов

Первый из параметрических методов – метод Берга, гораздо точнее оценивал результаты. Но он был не без недостатков: расщепление спектральных, эффект смещения спектральных, зависящий от начальной фазы гармоник. В ковариационных методах эти недостатки были устранены (рис. 3 слева – сигнал смеси 2-х синусоид с относительными частотами 0.3 и 0.34; SNR=30). Данные параметрические методы получили широкое распространение в ЦОС, поскольку они позволяют получать высокое разрешение и острые спектральные пики спектральных компонент. При низком порядке модели получаются более сглаженные спектральные оценки, при излишне высоком – увеличивается разрешение, но в спектре появляются ложные пики.

Авторегрессионные методы имеют гораздо лучшее разрешение спектральных компонент по сравнению с классическими методами спектрального оценивания. На рисунке (3)  справа очевидно превосходство параметрических алгоритмов ЦСА. Красной линией изображена периодограмма,  а синей линией – модифицированный ковариационный метод. Длина последовательности выбрана в 30 отсчетов. Спектр сигнала состоит из 2 спектральных пиков на частотах 0.3 и 0.35.

При использовании классических алгоритмов спектрального оценивания следует учитывать произведение «устойчивость*длительность*ширина полосы»; имеет место свойство обмена частотного разрешения на гладкость оценки; характерны эффекты маскирования и растекания спектра.

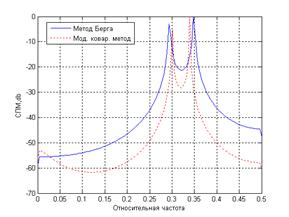
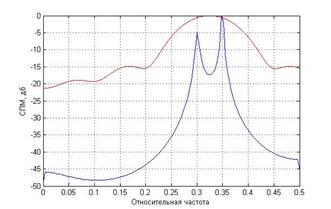
Рис. 3. Сравнение работы модифицированного ковариационного метода и метода Берга – слева. Сравнение качества оценивания двух спектральных компонент – справа

Увеличение порядка АР-модели сопровождается улучшением частотного разрешения, однако при избыточном порядке модели возникают ложные спектральные пики; для всех анализируемых методов характерно следующее свойство: при увеличении числа анализируемых отсчетов сигнала или порядка модели частотное разрешение повышается, однако дисперсия оценки СПМ увеличивается.

Интересным выглядит изучение информационной энтропии спектра сигнала. Как известно, энтропия шумового сигнала и речевого сигнала отличается, и, что можно отнести к преимуществам данного метода, энтропия мало чувствительна к амплитуде сигнала [5,6,7]. Принцип работы изображен на рисунке (4).

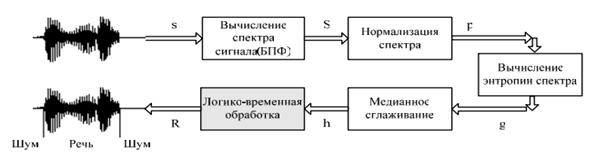
Рис. 4. Анализ речевого сигнала с использованием  энтропии спектра. Алгоритм

Как происходит обработка сигнала: сигнал дискретизируется, затем делится на сегменты по 256 цифровых отсчетов, перекрытие сегментов сделаем немногим более 25 % для устранения краевых сегментов. Мгновенные спектры мощности сигнала рассчитываем по следующей формуле:

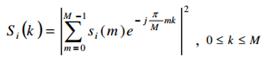                                                 ,                                   (10)

  М – размер сегмента сигнала.    

Дальше нормализуем спектр по всем частотным компонентам:

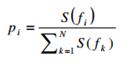                                                                                                                         (11)

Таким образом, мы получили плотность вероятности спектра.  Мы ее ограничиваем: верхним и нижним пределом. Если есть равномерное распределение частотных компонент – это белый шум, а также мы исключаем шумы в узкой частотной области.

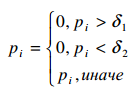                                                         ,                                                             (12)

  –  верхний и нижний пределы.

Из экспериментальных расчетов можно оценить порядок пределов как 0,01 и 0,3 при р от 0 до 1. Кроме того, в дополнение мы можем использовать и другие способы выделения сигнала из шума: методы спектрального вычитания и адаптивный фильтр Кальмана.

Мы рассматриваем энтропию как меру беспорядка в распределении, рассчитывая по следующей формуле:

                                           .                                                         (13)

Полученную функцию необходимо сгладить, используя медианное сглаживание. Данный тип сглаживания является наиболее устойчивым по отношению к случайным выбросам. Для этого берется какой-либо интервал [t-q,t+q] и вычисляется скользящая медиана в точке t. Медиана  ряда в интервале определяется  как  центральный  член  последовательности  значений  ряда, входящих  в  этот  временной  интервал,  упорядоченной  по  возрастанию. Как показывают эксперименты, наиболее точное вычисление медианы происходит при окне величиной в 5 сегментов. В том случае, когда мы вычисляем медиану в точках, близких к краю интервала и меньших, чем размер окна, приходится уменьшать окно [1].

Затем мы вычисляем порог для определения границ речевого сигнала.

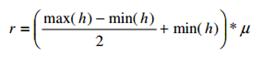                                                                             (14)

, µ – коэффициент зашумленности.

Он подбирается экспериментально, зависит от параметров шума. Данный коэффициент может принимать значения от 0,8 до 1,1 в зависимости от уровня шума. На основе вычисленного значения r выбираются акустические сегменты речевого сигнала.

Заключительным этапом является логическая временная обработка полученной энтропии спектра, используя допустимые на практике длительности речевых и неречевых сигналов, вычисленных ранее. Это необходимо, поскольку зачастую различные звуковые эффекты (кашель и прочее) принимают за речь, а некоторые участки речи за межречевой интервал. Используя адаптивный порог, можно определить сегменты речи на основе вычисления максимальной длительности межречевого участка S и минимальной длительности участка речи (рисунок 2).

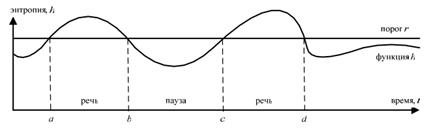
Рис. 5. Энтропия и порог обнаружения

Поскольку человек чисто физически не может произносить речевые фрагменты короче определенного значения, и так как всегда присутствуют паузы, можно экспериментально определить значения параметров R и S. Анализируем полученные результаты следующим образом:

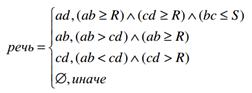                                        .                                       (20)

Если участок сигнала без речи содержит не более S сегментов, а участки, содержащие речь, составляют не менее R сегментов, то образуется сплошной речевой участок.

Экспериментальные расчеты показывают, что наименьший процент ошибок получается в случае узкополосного или белого шума – порядка 1,5 %. Наихудший результат – 16 % ошибок в случае розового шума, наиболее приближенного к реальной речи. К минусам данного метода можно отнести тот факт, что фоновая речь, пусть даже слабая, может быть принята за полезный сигнал. В целом данный метод довольно неплохо определяет речь в сигналах с высоким уровнем шумов и нестационарности.

 Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-07-00143.

Рецензенты:

Артемьев И.Т., д.ф.-м.н., профессор, зав. кафедрой математического и аппаратного обеспечения информационных систем (МиАОИС) ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова», г. Чебоксары;

Охоткин Г.П., д.т.н., профессор, декан факультета радиоэлектроники и автоматики (ФРЭА), ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова», г. Чебоксары.