За последние десятилетия быстро развиваются методы обработки и анализа информационных сигналов с применением вейвлет-преобразования [4]. Они позволяют исследовать свойства нестационарных сигналов, благодаря операциям масштабирования и сдвига. Разработаны вейвлеты для обработки изображений, обеспечивающие сжатие, декомпозицию, реставрацию, идентификацию изображений, а также удаление из них шумов. Имеются стандартные программные средства для осуществления вейвлет-преобразований функций в таких программных системах, как MATLAB, Mathcad, Mathematica [2,3].
Цель исследования
Целью проведенных исследований являлась разработка более быстродействующего алгоритма по сравнению с известными алгоритмами вейвлет-преобразования изображений при обеспечении требуемого качества преобразования.
Материал и методы исследования
В данной статье рассматривается результаты применения предлагаемого алгоритма вейвлет-преобразования изображений [6,7]. Информация об изображении представляется в виде двумерного сигнала и производится разложение изображения на множество уровней декомпозиции. Алгоритм характеризуется следующими особенностями:
1. Аналогично дискретному вейвлет-преобразованию гильбертово пространство сигналов L2(R) представляется совокупностью вложенных друг в друга подпространств. Порядок m подпространства определяет уровень декомпозиции сигнала[4].
![]() .
.
Размеры подпространств растут по мере уменьшения порядка m их уровня. Пересечение этих подпространств образуют пустое множество, а их объединение образует пространство L2(R) .
По мере уменьшения порядка подпространства обеспечивается выявление более мелких деталей сигнала, несущего информацию об изображении. Это позволяет переходить от более низкого к более высокому уровню разрешения изображения.
2. В качестве вейвлетов использованы производные функции Гаусса. Они имеют аналитическое описание, лучше локализованы во временной и частотной области, являются симметричными функции. Базисная функция является гладкой. Применение этих функций обеспечивает достаточно высокую точность вейвлет-анализа сигналов.
3. Для обеспечения возможности обработки сигнала в реальном масштабе времени расчеты параметров вейвлет-преобразования осуществляются с применением быстрого Фурье-преобразования.
Для вычисления вейвлет-спектра сигнала на основе производных функции Гаусса и функции Шеннона используется формула непрерывного вейвлет-преобразования:
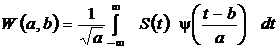 ,
(1)
,
(1)
где а – масштабный коэффициент, b – параметр сдвига вейвлета.
Для вычисления вейвлет-преобразования
прямым численным интегрированием требуется относительно много времени, поэтому
вейвлет-спектр вычисляется в частотной области с применением быстрого
преобразования Фурье (БПФ). При этом вычисляются коэффициенты
тригонометрического ряда ![]() ,
,![]() сигнала S(k) с использованием БПФ :
сигнала S(k) с использованием БПФ :
![]() (2)
(2)
![]() (3)
(3)
Вычисляются коэффициенты тригонометрического ряда a2(n), b2(n) вейвлета ψ(k) с использованием БПФ:
![]() (4)
(4)
![]() (5)
(5)
Вычисляется комплексно сопряженный спектр:
![]() ,
(6)
,
(6)
![]() .
(7)
.
(7)
Для четного вейвлета вычисляется левая часть суммы, для нечетного вейвлета ‑ правая часть суммы.
Вейвлет-спектр W(a,b) (матрица вейвлет-коэффициентов М×N) для входного анализируемого сигнала длиной N отсчетов получается путем вычисления М обратных преобразований Фурье от комплексно сопряженного спектра по формуле:
![]() .
(8)
.
(8)
При этом вейвлет-преобразование осуществляется для всего изображения, пилообразной разверткой по строкам и столбцам. В отличие от алгоритма Малла, данный алгоритм позволяет получать гораздо больше уровней разложения, тем самым позволяет более подробно исследовать изображение.
Устройство, реализующее алгоритм двумерного быстрого непрерывного вейвлет- преобразования, приведено на рис. 1, где: блок 1 – аналого-цифровой преобразователь (АЦП), блок 2 – оперативное запоминающее устройство (ОЗУ), блок 3 – блок развертки по строкам (РХ), блок 4 – блок развертки по столбцам (РУ),блоки 5, 6 – вычислители непре-рывного быстрого вейвлет-преобразования (НБВП), блок 7 – постоянное запоминающее устройство (ПЗУ), блок 8 – устройство управления (УУ).
Принцип действия устройства заключается в следующем. Анализируемый двумерный сигнал S(x,y) поступает на вход блока 1, с выхода которого полученная дискретная выборка S(n,n) поступает на вход блока 2.
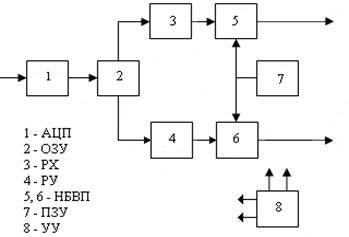
Рис.1. Блок-схема устройства двумерного прямого быстрого вейвлет-преобразования
С выхода этого блока двумерная выборка сигнала одновременно поступает на входы блоков 3 и 4, с выходов которых одномерные сигналы с количеством отсчетов n x n поступают на входы блоков 5, 6. С выходов этих блоков снимаются результаты вейвлет-преобразования сигнала в виде массива значений вейвлет-коэффициентов масштабов (М) и сдвигов (N). Блок 8 управляет процессом функционирования устройства.
Данное устройство позволяет выбирать для анализа двумерного входного сигнала различные типы вейвлет-функций с произвольным шагом дискретизации масштабных коэффициентов в блоке 7.
Устройство, реализующее алгоритм двумерного обратного быстрого непрерывного вейвлет-преобразования, приведено на рис. 2, где: блоки 1, 2 – вычислители непрерывного обратного быстрого вейвлет-преобразования (НОБВП), блок 3 – постоянное запоминающее устройство (ПЗУ), блоки 4, 5 – оперативные запоминающие устройства (ОЗУ), блоки 6, 7 – блоки преобразования одномерного массива в двумерный массив (ХП, УП), блок 8 – сумматор(СУМ), блок 9 – устройство управления (УУ).
Принцип действия устройства заключается в следующем. Два вейвлет-спектра W(m,n) поступают на входы блоков 1, 2, с выходов которых реконструированные сигналы S1(n), S2(n) поступают на входы блоков 4, 5. С выходов этих блоков сигналы поступают на входы блоков 6 и 7 преобразования одномерного сигнала в двумерный сигнал. Из блоков 6, 7, двумерные сигналы поступают на вход блока 8. В блоке 8 вычисляется сумма двух двумерных массивов, элементы которых предварительно делятся на два.
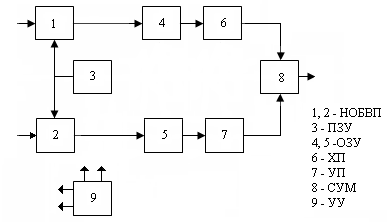
Рис. 2. Блок-схема устройства двумерного обратного быстрого вейвлет-преобразования
С выхода блока 8 снимаются результаты обратного быстрого непрерывного вейвлет-преобразования двумерного сигнала в виде массива значений S(n,n). Устройство управления обеспечивает взаимодействие блоков устройства.
Данное устройство позволяет выбирать различные типы вейвлет-функций с произвольным шагом дискретизации масштабных коэффициентов, хранящиеся в блоке 3 для синтеза двумерного сигнала.
Результаты исследования и их обсуждение
На рис.3 приведены результаты применения разработанного алгоритма для преобразования заданного изображения. Декомпозиция изображения выполнена на 18 уровнях. Изображение содержит 512х512 пикселей. В отличие от алгоритма декомпозиции сигнала Малла количество уровней разложения здесь в два раза больше, так как изображение обрабатывается не по строкам и колонкам, а пилообразной разверткой по вертикали и горизонтали. При обработке цветного изображения необходимо производить вычисление отдельно для каждого из цветов (красного, зеленого и синего). На этом рисунке представлены результаты разложения изображения на 1-ом, 3-ем и 7-ом порядках уровней декомпозиции. Из рисунка следует, что с увеличением порядка уровня подпространства мелкие детали изображения исчезают.
Для оценки полученных результатов на рис. 4 представлены результаты разложения этого же изображения на 2-ом, 4-ом и 5-ом порядках уровней декомпозиции с использованием алгоритма Малла с применением вейвлет Добеши-1, входящего в состав программных средств MATLAB [2,3].
Из визуального сравнения рисунков 3 и 4 следует, что качество преобразования изображения, полученное с использованием алгоритма Малла хуже, чем по рассматриваемому алгоритму. Это обусловлено тем, что дискретные вейвлеты несимметричные и негладкие функции.
 а)
а)
 б)
б)
 в)
в)
Рис. 3. Виды декомпозиции изображения, полученные с использованием
нового алгоритма при разных значениях m:a) –m = 1; б) – m = 3; в) – m = 7
В случае обратного вейвлет-преобразования сначала в заданном изображении представляются мелкие, а затем поэтапно добавляются крупные детали. Получаемое при этом изображение становится все более близким к оригиналу.
 а)
а)
 б)
б)
 в)
в)
Рис. 4. Виды декомпозиции изображения, полученные с использованием
алгоритма Малла при разных значениях m: a) –m = 2; б) – m = 4; в) – m = 5
Время вычисления рассматриваемого вейвлет-преобразования в частотной области определяется в основном вычислениями обратного быстрого преобразования Фурье комплексно сопряженного спектра сигнала и вейвлета, так как спектр сигнала вычисляется один раз, а спектр вейвлетов с разными масштабными коэффициентами можно вычислить заранее и хранить в памяти. Вычисление комплексно сопряженного спектра и последующее обратное БПФ для разных масштабных коэффициентов занимает основное время ВП. Вейвлет-спектр при больших масштабных коэффициентах имеет почти одинаковое значение для многих значений параметра сдвига, поэтому нет необходимости вычислять ВП для каждого значения параметра сдвига, не превышая интервал Котельникова-Найквиста.
Заключение
Рассматриваемый алгоритм вейвлет-преобразования может быть использован во многих задачах преобразования изображений. Такими задачами являются обзорные операции, определение параметров объекта, идентификация и распознавание объектов, определение координат, сжатие информации об изображении. Таким образом, рассматриваемый алгоритм обработки сигналов является удобным для применения, относительно простым в реализации и обладает существенным быстродействием, при обеспечении требуемого качества преобразования изображений.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта №14-07-00143
Рецензенты:Артемьев И.Т., д.ф.-м.н., профессор кафедры математического и аппаратного обеспечения информационных систем, ФГБОУ ВПО «ЧГУ им. И.Н.Ульянова», г. Чебоксары;
Славутский Л.А., д.ф.-м.н., профессор кафедры управления и информатики ФГБОУ ВПО «ЧГУ им. И.Н.Ульянова», г. Чебоксары.
Библиографическая ссылка
Павлова Н.В., Григорьев В.Г., Семенов В.И., Желтов П.В. АЛГОРИТМ ДЕКОМПОЗИЦИОННОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЙ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16273 (дата обращения: 19.04.2024).



