Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Математическое моделирование образовательного процесса наталкивается на сложности его математического описания в едином пространстве для всех уровней профессиональной подготовки. Действительно, в процессе обучения в соответствии с предметно-ориентированным и компетентностным подходами на различных курсах обучающиеся изучают множество разнообразных предметов. При таких подходах математическое моделирование возможно либо в пространстве всех изучаемых предметов (количество координат определяется количеством изучаемых предметов), либо отдельно по каждому предмету, либо в пространстве предметов семестра или курса. При этом, учитывая, что по мере обучения изучаемые дисциплины от семестра к семестру изменяются, пространство координат математического моделирования образовательного процесса постоянно изменяется. Это обусловлено тем, что ни дисциплины, ни компетенции не могут быть приняты в качестве системообразующей основы математического моделирования образовательного процесса.

Авторы предлагают метод и комплекс программ математического моделирования образовательного процесса в пространстве вектора знаний [1]. Причём вектор знаний объединяет в единую систему компоненты, которые характерны как для всех видов деятельности, производства и технических проектов, так и для всех предметов и компетенций направления подготовки [3,6]. Это позволяет проводить моделирование в целом образовательного процесса на любом временном отрезке в едином векторном пространстве.

Основные положения

Для математического моделирования образовательного процесса на любом временном отрезке разработана математическая модель образовательного процесса [3,6], описывающая познавательный процесс как целостную систему накопления, совершенствования и повышения уровня и качества знаний в едином векторном пространстве, объединяющем математико-методологическую, технико-технологическую, организационно-экономическую; информационно-программно-алгоритмическую и культурно-воспитательную компоненты вектора знаний (v1, v2, v3, v4, v5)  [1,3,5].  Все составляющие учебного процесса, в том числе и дисциплины на всех стратах обучения описываются в пространстве компонент вектора знаний. Основу организационно-экономического модуля направления подготовки «Автоматизация и управление» составляет множество предметов, обеспечивающих формирование у обучающихся базовых знаний в контексте организационно-экономического компонента, начиная от детализации через обобщение к специализации  по стратам обучения [7]. Представление всего комплекса дисциплин в векторном пространстве знаний обеспечивает моделирование образовательного процесса во взаимосвязи всех составляющих учебного процесса. При этом на протяжении всего периода обучения определяющей экономические знания для всех дисциплин специальности является организационно-экономическая компонента.

Для математического моделирования механизма управления познавательной деятельностью обучающегося на всех стратах обучения в пространстве единых независимых управляемых координат, устанавливающих уровень знаний в целом по специальности, предполагается определение структуры объекта управления (ОУ) [2]. Моделирование познавательного процесса основывается на представлении обучающегося как объекта управления (рисунок 1) в векторном пространстве знаний [4].

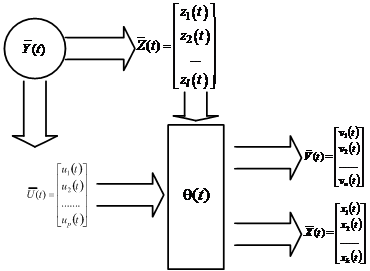
Рисунок 1. Структурная схема объекта управления

Здесь за выходные координаты по организационно-экономическому компоненту приняты: управляемые координаты  – это достижение поставленных целей – овладение знаниями (теоретический материал и задачи) и  – вектор состояний организационно-экономического компонента – характеризует текущее состояние объекта в процессе обучения (количество и качество знаний и навыков по организационным и экономическим вопросам).  – совокупность входных координат, включающих:  – управляющие координаты (мотивация, цели, задачи, методика и содержание обучения) и  – возмущающие воздействия, Q4(t) – внутренние динамические параметры объекта (обучающегося).

По каждому компоненту вектора знаний внутренние динамические свойства по восприятию информации обучающихся можно представить моделью -ого порядка в виде передаточной функции в канонической форме

или  моделью в нормальной форме пространства состояний

;

.

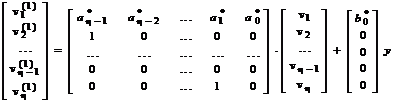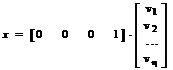Размерность вектора знаний может быть произвольной и для большинства специальностей она не превышает пяти или шести [4,6]. По времени и по характеру обучения процесс обучения распределён на отдельные этапы (лекции, лабораторные, практические и другие виды занятий). В пространстве состояний выбранных компонент вектора знаний процесс обучения представим в виде дискретной модели

.

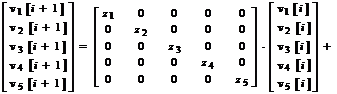
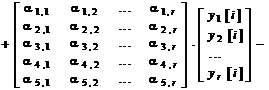
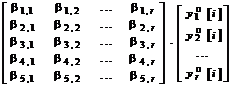Период дискретизации может быть принят равным одной неделе.

Приведённые математические модели отражают внутренние свойства обучающихся, их возможности и скорость восприятия информации по каждому компоненту вектора знаний.

Цель исследования

Цель данного исследования в том, чтобы создать комплекс программ, обеспечивающий математическое моделирование образовательного процесса по организационно-экономическому компоненту в координатном пространстве вектора знаний.

Для задач математического моделирования образовательного процесса по организационно-экономическому компоненту (ОЭК) вектора знаний [2] предлагается создать специализированный комплекс программ, встраиваемый в разработанный в ПензГТУ единый интегрированный комплекс сетевых автоматизированных лабораторий (ИКСАЛ), позволяющий объединять все виды научной и учебной деятельности вуза в единую систему[2, 3].

Программный комплекс является модульным приложением, которое позволяет загружать данные посредством взаимодействия с SQL-сервером. Каждый модуль может использоваться во всех программных компонентах ИКСАЛ за счёт различных наборов сервисов [2].

Модульное приложение структурировано в трёх уровнях (рисунок 2).

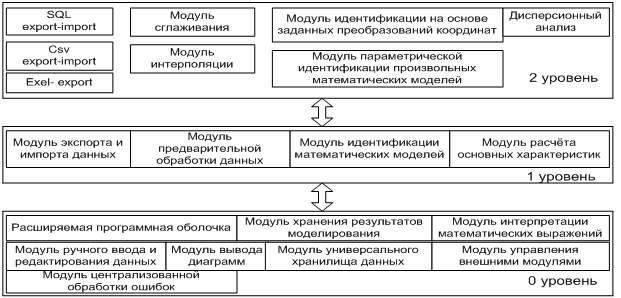
Рисунок 2. Уровни программного комплекса построения математических моделей

В нулевой уровень входит расширяемая программная оболочка (РПО) которая представляет собой основной набор функций, а также общий графический web-интерфейс, обеспечивающий управление математическим моделированием объектов специальности в контексте всех компонент вектора знаний, в том числе и в контексте ОЭК.

В первый уровень включены модули, поддерживающие встраиваемые в интерфейс графические и функциональные оболочки для дополнительных модулей второго уровня.

На базе сервисов второго уровня реализуются модули с рабочими процедурами расчёта и моделирования [2].

Рассмотрим назначение и возможности модулей [1,2,4,6].

Для хранения результатов моделирования используется модуль хранения результатов моделирования – качественные и количественные характеристики отобранных функциональных наборов, произведённых модулями первого уровня. Программные вычисления значений пользовательских форм математических моделей для параметрической идентификации выполняет модуль интерпретации математических выражений. В ОЭК этого модуля включены  процедуры моделирования анализа и  оценивания объектов специальности в пространстве организационно-экономических индикаторов.

Модуль ручного ввода и редактирования данных позволяет в удобной форме вводить и редактировать экспериментальные данные и создавать сложные, зависимые таблицы с наборами результативных и определённых признаков. ActiveX интерфейс реализуется в модуле диаграмм и графиков, дающем графическое представление данных, находящихся в системе. Единые компоненты встроенной поддержки диаграмм, используются для представления информации всеми модулями системы. Иерархию связей между таблицами позволяет хранить модуль универсального хранилища данных и является сервисным интерфейсом к реляционной базе данных на основе SQL-сервера. Данные таблиц используются для процедур обработки множества экспериментальных массивов и в процессе предварительной обработки экспериментальной выборки.

Для вывода и фиксации сообщений об ошибках служит модуль централизованной обработки ошибок, т.к. модули расширения создаются разными разработчиками и необходимо разработать и применить однотипный подход к обработке ошибок.

Модули первого уровня обнаруживаются, регистрируются и загружаются модулем управления внешними модулями, который представляет интерфейсы для обратного взаимодействия с РПО.

Модуль экспорта и импорта находится на первом уровне системы и обеспечивает загрузку и активизацию модулей экспорта и импорта второго уровня, что позволяет расширять возможности комплекса за счёт разработки новых модулей «конвертеров».

Модуль предварительной обработки информации осуществляет загрузку модулей сглаживания и интерполяции второго уровня. Для доступа к рабочим процедурам предоставляется графический интерфейс, взаимодействующий с интерфейсом РПО.

Авторская методика [1,2,4] построения однофакторных и многофакторных зависимостей реализована в модуле идентификации математических моделей, также представляет собой графический интерфейс, взаимодействующий с интерфейсом РПО, осуществляет загрузку и регистрацию модуля идентификации на основе заданных преобразований координат и модуля параметрической идентификации математических моделей заданной формы [3,6].

На основе входных данных по индексу таблицы данных и буфера результатов моделирования модулём расчёта основных статистических характеристик формируются отчёты со статистическими характеристиками, характеризующими данные и модели.

На основе заданных преобразований координат модуль идентификации осуществляет с требуемой точностью процедуру идентификации на основе входной информации: уровня преобразований и индекса таблицы с экспериментальными данными. При этом выполняется следующая последовательность: перебор сочетаний преобразований координат и преобразование в соответствии с ними результативного признака таблицы с экспериментальными данными; оценка параметров математической модели; проверка диапазона точности и, в заключение – синтез вида математической модели на основе преобразования координат.

Модуль параметрической идентификации математических моделей заданной формы решает задачи параметрической идентификации с n параметрами. Возможен выбор конкретного метода оптимизации: методы золотого сечения, деления отрезка пополам, градиентного спуска с полиномиальной аппроксимацией по координатам, Фибоначчи. Входными параметрами являются: структура математической модели, шаг оптимизации, начальные значения параметров и заданная точность расчёта.

Выводы

Программный модуль моделирования объектов специальности обеспечивает решение задач образовательного процесса на всех стратах обучения по организационно-экономическому компоненту.[7]

Разработанный комплекс программ математического моделирования объектов специальности представляет единую систему, обеспечивающую проведение исследований, как объектов специальности, так и самого образовательного процесса в едином векторном пространстве знаний с использованием элементов математического и физического моделирования [2].

Методика формирования управляемых координат образовательного процесса – вектора знаний, основана на анализе видов деятельности выпускников специальности, структур предприятий и типовых проектов по рассматриваемой специальности и требует выявления предметных составляющих – в данном случае – организационно-экономического компонента [6].

Возможность математического и физического моделирования систем управления и технических объектов, различающихся как по физическим законам, так и по динамике протекания процессов, т. е. многофункциональность, позволяющая моделировать и образовательный процесс в вузе, является главной особенностью интегрированного комплекса сетевых автоматизированных лабораторий [5].

 

Рецензенты:

Кошев А.Н., д.х.н., профессор кафедры «Информационно-вычислительные системы» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.

Мачнев В.А., д.т.н., профессор, профессор кафедры «Основы конструирования механизмов и машин» ФБГОУ ВПО «Пензенская государственная сельскохозяйственная академия», г. Пенза.